- 戈特洛布·弗雷格(Gottlob Frege)的半身像
經驗主義和理性主義,數學哲學中最重要的兩個觀點
這是數學哲學中兩個最基本的觀點。因此,我可以簡單地說,任何一位數學哲學家都必須對這兩種觀點表態,戈特洛布-弗雷格(1848-1925)討論了密爾的經驗主義思想和康德關於數學性質的理性主義思想,並在他的《算術基礎( The Foundations of Arithmetic)》中為自然數提出了一個新概念:對數的概念的邏輯數學探究。
弗雷格的自然數的概念
客觀的東西,比如說“北海的面積是1萬平方英里,那麼無論是‘北海’還是‘1萬平方英里’,我們都沒有提到我們頭腦中的任何狀態或過程”:相反地,我們在說一種相當客觀的東西,這種客觀的東西獨立於我們的理念和一切思想之外。
但是,儘管他說的是客觀性,否定我們頭腦中的過程,但他根本就不是一個經驗主義者。對他來說,每個自然數的概念都應該只用數學和邏輯的物件來構建。主要是因為根據他的說法:
一個命題為真和它被認為的是不一樣的。
也就是說,與純粹的心理學(和經驗學)物件不同,僅僅因為某個東西被認為或存在,並不意味著它在邏輯和數學中是真的。
對弗雷格來說,數學和邏輯物件具有不同的性質,它們是純粹的分析性的,按照他的說法,將一個命題歸類為綜合命題或分析命題的最好方法是看看使這樣一個命題成為真的或假的理由。也就是說,如果一個命題需要經驗元素才能成真,它就是綜合的,如果不需要,它就是分析的。他說:
在我看來,先驗和後驗、綜合和分析之間的這些區別並不涉及判斷的內容,而是涉及作出判斷的理由(FREGE, 1980, p.3 / §3)。
現在讓我們看看弗雷格是如何闡述數字0、1以及所有其他自然數的概念的。
自然數 "0 "的概念
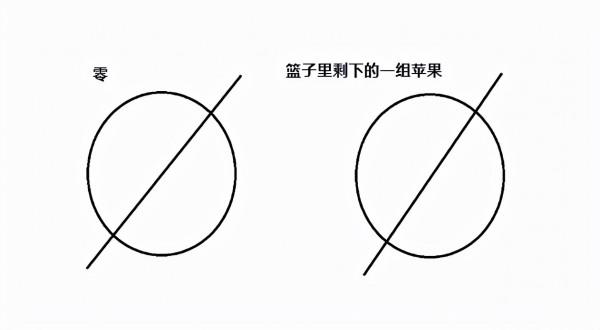
“0”的概念是指沒有與自己相同元素的集合,與其他沒有屬於它的元素的集合相比,它就像一個“數字”。
因此,當你說 "籃子裡沒有蘋果了 "時,根據弗雷格的數學哲學,你是在將 "籃子裡剩下的所有蘋果的集合 "與弗雷格的零概念進行比較。
自然數 "1 "的概念。
至於數字1,弗雷格指出,兩個相鄰數字的概念必須以某種方式聯絡起來。在《算術基礎》中,弗雷格說:
為了證明自然數的數列中每一個數後面都有一個數,我們必須提出一個數的概念,這個數就屬於這個數 。
為了滿足這一點,他指出,按照自然數的順序,作為自然數概念的集合必須包含所有最小的自然數概念的 "擴充套件 "之和。所以這個數字包含在1的概念中,因此,有助於構成“數字1”的弗雷格定義的是它更小的相鄰數——數字0。
1是屬於 "與0相同 "的概念的數。
請注意,這使得 "自然數1 "的概念只包含一個元素(0),而這樣的概念允許我們在純分析的條件下確定什麼是 "自然數1"。
那麼,當你將弗雷格的自然數1的集合與另一個只有一個元素屬於它的集合進行比較時,你就成功地將弗雷格的自然數1的概念作為一個自然數。或者,你將使用弗雷格的自然數1的概念作為另一個集合的分類。
弗雷格的其他自然數的概念。
其餘數字的概念也是根據所有 "前面的數字 "的 "延伸 "得到的,見圖片。
三個重要的概念。基數、外延和等數
為了對這些概念有一個更完整的理解,讓我們來看看基數、外延和等數的概念。這三個概念被弗雷格認為是如下:
基數是指找到一個集合的基數的可能性,它將根據屬於一個集合的元素的和來度量(定義)。例如,在康託的集合理論中,這個概念(基數)允許我們說某些無窮大比其他無窮大大。
等數的概念表示具有相同基數的集合之間存在相等的可能性。弗雷格對這個概念的理解如下:
屬於F概念的(基數)數與屬於G概念的(基數)數相同(相等),只要F的物件與G的物件之間存在一一對應的關係。
弗雷格還對 "等數 "的概念作了進一步的解釋:
如果直線a與直線b平行,那麼 "與直線a平行的直線 "這一概念的外延就與 "與直線b平行的直線 "這一概念的外延相同;反之,如果剛才提到的兩個概念的外延相同,那麼a就與b平行。(......)要把這一點應用於我們自己的數的情況,我們必須用直線或三角形的概念來代替平行或相似,把屬於一個概念的物件與屬於另一個概念的物件一一對應起來的可能性。為簡潔起見,當這個條件得到滿足時,我將說概念F等於概念G。
至於“外延”的概念,我想說的是,它是連線基數和等數概念與量化的關鍵概念。弗雷格用“外延”這個詞來聯絡“函式”和“物件”,在他看來,概念F的外延就是“概念F的值的過程”。
但 "值的軌跡 "是什麼意思?例如,笛卡爾平面上一個函式的x軸和y軸都可以包含自然數的升序。
弗雷格的理性主義和他對經驗主義的論證
正如我們在上一節中所看到的,弗雷格在他的定義中只採用了分析性元素。他並不像米爾那樣明確地訴諸經驗主義的概念。根據米爾的說法,數學計算是觀察事實的一個結果。他說:
(......)計算不是來自定義本身,而是來自觀察到的事實問題。
對此,弗雷格回答說:
根據米爾的觀點,我們實際上不可能把1,000,000=999,999+1,除非我們觀察到一系列的事物正是以這種奇特的方式分裂開來。
弗雷格還在《算術基礎》中指出,這種嚴格的經驗主義算術觀將難以解釋數字 "零 "和 "1"。畢竟,有什麼 "物理事實 "可以給自然數0和1以經驗上的支援?
弗雷格的自然數概念是最充分的嗎?
弗雷格使用新的形式資源(集合和命題函式)來創造新的邏輯哲學。在某種意義上,他的工作比皮亞諾的工作更深入,皮亞諾也試圖制定算術推理的基礎(見皮亞諾的五個公理)。
然而,弗雷格也面臨問題。羅素悖論和哥德爾定理使康托爾的集合論,以及整個邏輯主義看起來有缺陷。
事實上,甚至在哥德爾不完備性定理之前,就已經有了反對弗雷格的數學基礎的有力論據。例如,龐加萊(1854-1912)指出了形式主義和邏輯主義的弱點,正如格雷所承認的,龐加萊在他的一些批評中 "被證明是正確的"。
關於 "弗雷格與康德 "辯論的幾點說明
弗雷格沒有像斯圖爾特-米爾那樣把他的數學哲學建立在具體的量綱上,他也不同意康德關於數學命題具有綜合性質的觀點。如我們所見,弗雷格選擇了一個純粹的數學分析基礎。
然而,這並不簡單,比如說,"空間和時間"(康德認為是直覺的純粹形式)將無助於構成弗雷格的數的概念。畢竟,例如,弗雷格使用 "外延 "的概念來實現他的自然數的概念,而 "外延 "是一個與空間概念極其接近的概念。弗雷格甚至在幾何推理中使用了這個術語,他說:
如果直線a與直線b平行,那麼 "與直線a平行的直線 "這一概念的延伸與 "與直線b平行的直線 "這一概念的延伸是相同的。
因此,我認為弗雷格與康德思想的關係更值得關注。