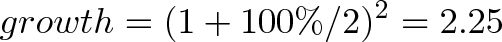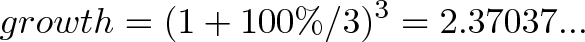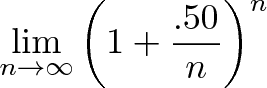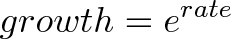世界第八大奇蹟-複利

一個關於發財的故事

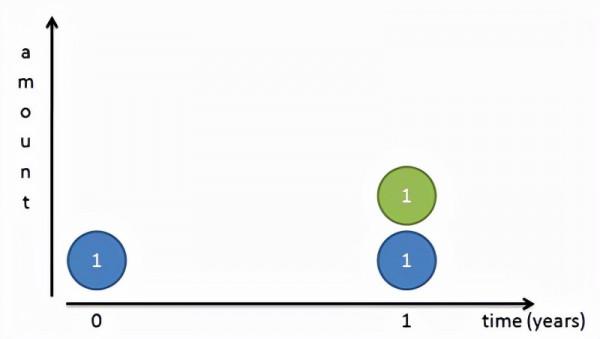
假如你開了一家銀行，承諾儲戶每年的存款利率是100%，也就是說，只要儲戶在你這裡存了1個億，一年後儲戶就能拿走2個億：

儲戶自然是賺了大錢，那麼你又該怎麼賺錢呢？

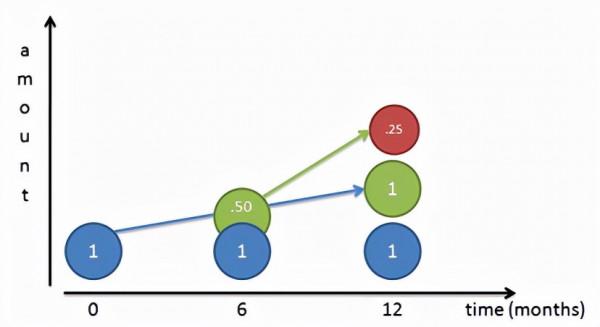
你可以把儲蓄存在你這裡的錢存到另一家銀行去，當然不能只存一年，你可以只存半年。當你半年後去銀行取錢，銀行總不能把你的存款白用半年，它必須給你利息，那麼這個利息該怎麼算呢？對，給你50%的利息比較合理，因為你只存了半年。然後你馬上把你的本金和利息加在一起，再存到另一家銀行去。到年底，你一算，你一共可以得到：

在支付掉你的儲戶的2個億後，你發現你淨賺了0.25億，這就是2500萬啊，而你要做的僅僅是多跑了兩趟銀行，完全的空手套。

發財秘訣的關鍵在哪裡？

在一般人的眼裡，如同那個儲戶，只看到自己存1個億，一年後能拿回2個億就開心的不得了了。他們的腦海裡是這樣想的：

這是用靜態的眼光來看問題，而更聰明的你則用動態的眼光來看問題，這新增加的1個億不應該是在年底的最後一刻才冒出來的，它應該是用了一年的時間慢慢地生長出來的，你的腦海裡是這樣想的：

既然錢能生錢（新錢），那麼這些新生的錢自然也能生新的錢（新新錢），於是你得到了一個賺錢的秘訣：

沒錯，每隔半年存一次多出來的2500萬就是這麼來的。寫成公式：

如果你每隔季度存一次呢？那就是下面的樣子：

那麼你能淨賺大約3700萬，寫成公式：

這是不是一個bug？

你感覺自己發現了一個天大的秘密，那就是只要錢多週轉一次就能賺得更多。自然，你會想到，如果你每天存一次呢？每小時存一次呢？每分鐘存一次呢？。。。

到這裡，你應該可以想到一個可怕的可能：你會不會賺得比你的儲戶還多？

畢竟人家賺了1個億那可是要出真金白銀的1個億本金的，而你從頭到尾就是個空手套，如果你能賺得比你的儲戶還多，那還有天理嗎？

為了得到更準確的答案，你繼續你的計算：

n          (1 + 1/n)^n
------------------
1          2
2          2.25
3          2.37
5          2.488
10         2.5937
100        2.7048
1,000      2.7169
10,000     2.71814
100,000    2.718268
1,000,000  2.7182804
...

你失望的發現，無論是如何頻繁地倒手，你淨賺的錢總會趨於一個極限值2.7182804...，也就是說你最多最多隻能淨賺7182萬，你不可能賺的比你的儲戶還多。

與你的沮喪失落不同，數學家看到了你的計算則欣喜若狂，因為你居然發現了一個數學常數。

好了，該數學家登場了，雅克比·伯努利得到了一個足以載入史冊的公式：

這確實是一個常數，約等於2.71828182845904523536...。

就這樣，一個小學生的算術問題硬生生地變成了一個大學生的高數問題。

事情發展到這裡，你不禁感慨，這居然不是一個bug，不僅僅是天理還在，而且這玩意本身居然就是天理的一部分。

改變一些條件會如何？

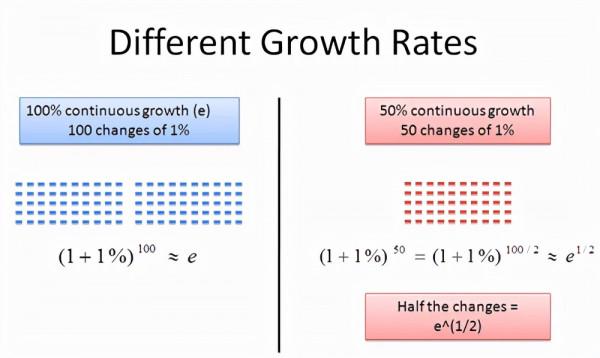
你的發財大計自然不會是一帆風順的，100%的存款收益率實在是太高了，比很多高利貸都黑。那麼改變一下存款收益率會如何呢？例如改為50%。

還好，還好，錢雖然不能掙得更多了，但。那麼，這個秘訣的關鍵在哪裡呢？

讓我們來簡單算一下：

也就是：

用圖表示就是：

類似的，我們可以將存款收益率修改為任何數字rate（例如50%、25%、200%），我們得到了一個更通用的公式：

儘管存款收益率50%低了些，但是誰說我們只掙一年錢呢？還是假定存款收益率為300%，如果我做兩年呢？

這依舊是一個指數級的增長，更一般的公式：

複利

看到這裡，恭喜你，你已經學會了複利，一個被"愛因斯坦稱之為世界第八大奇蹟"的玩意兒：

哎，這玩意兒不就是高利貸的“利滾利”嗎？街頭混混都懂的小玩意，還用驚動愛因斯坦？

對，就這兒，別小看這玩意，複利公式包含了能使我們財務自由的最核心的秘密。

再次複習一下複利公式：

這裡的關鍵因素只有三個：

本金，大多數人都知道本金越大掙錢越容易，但相應的，如果是賠錢的話那也會賠得越多，那如果你的本金本身就是炸鍋賣鐵高槓杆借來的，那就自求多福吧
增長率，大多數人都喜歡高增長率的專案，但是高增長率的專案往往也意味著高風險，短時間的高增長率專案和長時間的低增長率專案最終受益都是一樣的，穩一穩也不失一種明智的選擇
時間，時間對於所有的人都是一樣的，但早啟動和晚啟動那差異可就大了

實際上，我們自身也可以看做是一個專案，利用複利的思維投資自己也是一個不錯的選擇，但關鍵是你得有那份自律。古代的先賢們早已有了這種明悟：