明明是定理，卻被稱之為悖論——斯梅爾的反常悖論

當我們遇到一些違反常識又的確發生的事件時，我們會說什麼來表達自己的驚訝之情呢？曉然菌先來：“我擦，這也行？”事實上，在數學上反直覺的事情還是很少的。絕大部分數學理論的由來，都是先發現某個現象，然後從理論上證明出這樣存在的合理性。就好比哥德巴赫猜想一樣，雖然幾百年都不能完全證明，但是這玩意看起來就像是對的，如果最後被完全證明，我們的反應應該是，今天終於能完成了！但如果後面有位大神突然之間發現了一個反例，你想想在數學界會掀起什麼樣子的波瀾！

我擦，這也行？

今天也說個比較違反常識的數學理論，雖然已經被完全證明了，但是有些人還是願意把這個違背常識的現象稱之為悖論。

話說在1930年的美國密歇根州弗林特市，有個叫斯蒂芬·斯梅爾（Stephen Smale）的小朋友出生，這位小朋友心智健全，資質平平，18歲就考上州立大學。老實說，在上大學本科這幾年，斯梅爾其實也沒啥特別突出的地方，跟普通人無異，事實上我懷疑，如果斯梅爾後來不讀研究生，那麼斯梅爾後面可能會從事跟數學完全無關的工作。

密歇根大學

不過好在1957年，斯梅爾硬著頭皮讀到了博士，並且跟了一位相當厲害的老師，在這位老師拉烏爾·博特（Raoul Bott）的教導下，斯梅爾厚積薄發，逐漸開始成長為一位出色的數學研究者。

1958年，小夥子斯梅爾拿著一篇論文去給領導博特看，斯梅爾聲稱他證明了在不撕裂球面，不折起球面的情況下，可以使一個球面內部完全外翻到外面來，且不破壞球面的任何一個部位！導師博特在看到這篇論文的最終目的時，他的反應就跟在座的你我一樣，這怎麼可能？在不破壞球面的情況下，將球的內部完全外翻到外表面。

當年意氣勃發的斯梅爾

斯梅爾強調，這個球表面在處理的時候，不能撕裂，不能摺疊，但是球面可以與自身相交。聽到這個條件之後，博特開始仔細檢視論文研究中的方法，最後他得出了一個無可辯駁的事實。這個震驚世界的理論是對的，斯梅爾是對的，直到現在博特才發現，斯梅爾同志本科時期那些種種庸碌無為的表現其實都是在積累自己，等到某個時刻集中力量爆發，而現在就正是這個時候。

不破壞球面的情況下外翻球面可能嗎？

斯梅爾的研究其實在當時有著濃厚的學術背景的，20世紀前50年，正是拓撲學這一數學分支的黃金髮展時代。你能想象，美國政府在撥給數學研究界的經費有一半都投給了拓撲學分支嗎？數學發展到現在的水平，分支學科，沒有一百多也有好幾十個吧。對於拓撲學也太厚愛了吧，也正因為如此，在那幾十年，誕生了相當多數量的拓撲學大師，比如龐加萊，陳省身，還有胡列維茨等等。

導師 拉烏爾·博特

斯梅爾發表這篇內球外翻的論文也是斯梅爾開始成為上面那些拓撲大師的開始。

拓撲學家眼裡甜甜圈和咖啡杯是一樣的

我們來看看這個內球外翻有哪些要求：

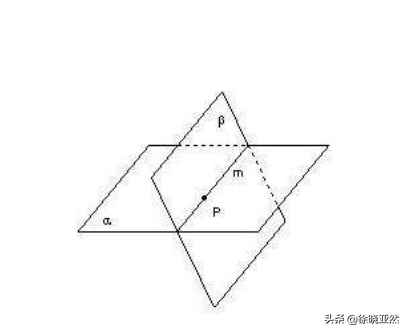
首先，你不能把球面撕裂，不能摺疊，但是你在變換的過程中是可以使得球面與自身相交的，且相交之後可以互為內外表面。

我們感覺覺得斯梅爾的這個結論是悖論的前提是，前面兩個前提太上頭了，沒有人會覺得這是可以成功的，事實上，假若斯梅爾的內球外翻就只有前兩個前提，那確實是不可能的。但是往往我們也忽略了第三個前提，球面可以與自身相交。這個就比較抽象了，什麼叫球面可以與自己相交？事實上，這個操作在現實裡是不可能的，哪怕你就用兩張紙來做模擬，也就只能貼合在一起而已。但是這個操作在數學上卻輕而易舉，想想高中時代學的立體幾何，兩個面相交這不是常規前提嘛。

實際上我們很難用實物去表示面與面相交

現在前提我們都瞭解了，那具體要怎麼做才能實現所謂的內球外翻呢？這一點上，斯梅爾的論文只是給出了這種方法的存在性，論文中卻並沒有給出一個具體的方法。大家可千萬不要覺得存在性的證明不重要，基本上存在性的問題一旦確定下來，下面再去找最終的答案就有了完全的方向了，存在性的證明就相當於是從0到1，而具體答案的破解則是1到2,2到無窮大了。萬事開頭難。

2008年 斯梅爾

事實上，這樣的方法不但存在，還不止一種！不過鑑於需要極致的空間想象能力，下面的動圖是一個普通的解法，如果想象不到，我在文章底下會貼出一個出自明尼蘇達大學幾何中心製作的關於內丘外翻答案的影片地址，這也是目前我認為做得最好的講解影片。

斯梅爾內球外翻的一個解

內球外翻的理論也成為了斯梅爾同志職業生涯的代表作，這還遠未到達巔峰。3年之後，斯梅爾同志釋出了5維及5維以上龐加萊猜想成立的論文，也正是這個再次震驚世界的結論讓斯梅爾同志獲得了1966年的菲爾茲獎。值得一提的是，斯梅爾的這篇關於龐加萊猜想的部分證明成果，也是關於龐加萊猜想證明過程中第一個重大具有里程碑式意義的事件。

20世紀的拓撲學基本上哪兒都有我 龐加萊

有不太熟悉拓撲學的同學會問，龐加萊猜想是什麼，有這麼重要嗎？曉然菌就這麼說吧，龐加萊猜想在拓撲學中的地位就相當於微積分在數學分析學中。菲爾茲獎評獎委員會單單在龐加萊猜想的證明過程上就給了3次獎，他們分別是，1966年的斯梅爾證明了5維及5維以上的龐加萊猜想成立，1982年的美國數學家麥克·弗裡德曼證明了4維猜想，以及2006年的俄羅斯人佩雷爾曼大神的最終證明。

菲爾茲獎數量的多少就能看出龐加萊猜想多重要

明明這是一個無可辯駁的事實，卻被人們還是稱之為斯梅爾悖論，說起來還真有點委屈。不過前面有個眼睜睜的例子，費馬大定理在沒被證明之前，就被稱之為大定理。也許，人們總是會給他們最感興趣的問題起一個最特別的名字吧。