有界磁場的作用:利用有界磁場可以控制帶電粒子的運動方向.
【思路】
在粒子運動過程分析(正確畫出運動軌跡示意圖)的基礎上藉助幾何關係先確定最小區域示意圖,再利用幾何關係求有界磁場區域的最小面積.
確定圓心經常用到的是圓心在入射速度和出射速度夾角或夾角補角的角平分線上.
一些結論:
①粒子射入、射出磁場邊界時的速度的垂線的交點即軌跡圓圓心.
②所求最小圓形磁場區域的直徑等於粒子運動軌跡的弦長.
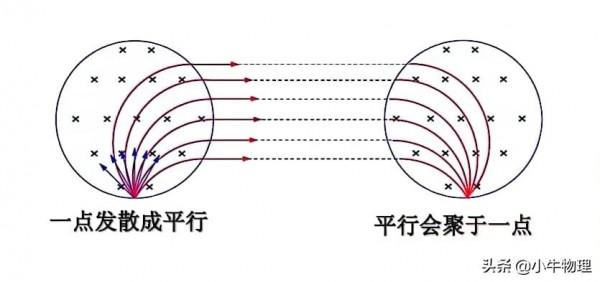
③從同一點入射的速率相同的粒子,若要求出射後粒子運動方向都平行,則磁場中粒子出射位置所在的邊界是一段圓弧,其半徑與粒子在該磁場中運動的軌跡半徑相等,且圓心與入射點的連線垂直於出射方向(磁聚焦).反之亦然(磁發散).
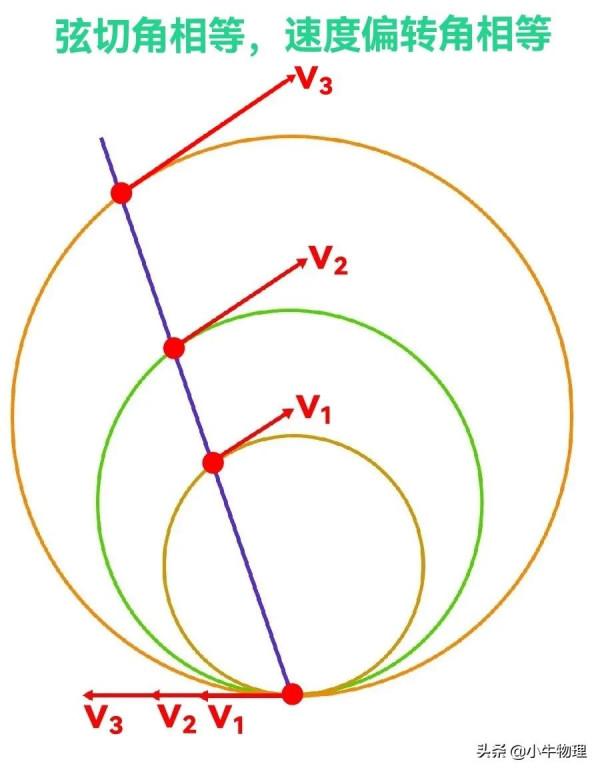
④從同一點沿相同方向入射的不同速率的相同粒子,若要求出射後粒子運動方向都平行,則磁場中粒子出射位置所在的邊界是一段線段.線段的兩個端點分別在入射點及速率最大的粒子的出射點上.
【步驟】:
①畫出粒子運動的可能軌跡
②確定磁場一定要覆蓋軌跡
③找到軌跡兩端與磁場形狀
【方法】:
①放縮圓、旋轉圓、平移圓
②幾何法
③引數法
例題:如圖所示,在傾角為30°的斜面OA的左側有一豎直檔板,其上有一小孔P,OP=0.5m.現有一質量m=4×10⁻²⁰kg,帶電量q=+2×10⁻¹⁴C的粒子,從小孔以速度v₀=3×10⁴m/s水平射向磁感應強度B=0.2T、方向垂直紙面向外的某磁場區域.且在飛出磁場區域後能垂直打在OA面上,粒子重力不計.
(1)若磁場是方向垂直紙面向外的一圓形磁場區域,圓形磁場區域的最小半徑.
(2)若磁場是方向垂直紙面向外的一矩形磁場區域,求矩形磁場區域的最小面積.
(3)若磁場區域為正三角形且磁場方向垂直向裡,粒子運動過程中始終不碰到擋板,其他條件不變,求此正三角形磁場區域的最小邊長.
例題:如圖,ABCD是邊長為a的正方形.質量為m、電荷量為e的電子以大小為v₀的初速度沿紙面垂直於BC邊射入正方形區域.在正方形內適當區域中有勻強磁場.電子從BC邊上的任意點入射,都只能從A點射出磁場.不計重力,
求:
(1)此勻強磁場區域中磁感應強度的方向和大小;
(2)此勻強磁場區域的最小面積.
例題:如圖所示,一帶電質點質量為m,電量為q,以平行於x軸的速度v從y軸上的a點射入圖中第一象限所示的區域。為了使該質點能從x軸上的b點以垂直於x軸的速度v射出,可在適當的地方加一個垂直於xOy平面、磁感應強度為B的勻強磁場。若此磁場僅分佈在一個圓形區域內,試求此圓形磁場區域的最小半徑。(重力忽略不計)
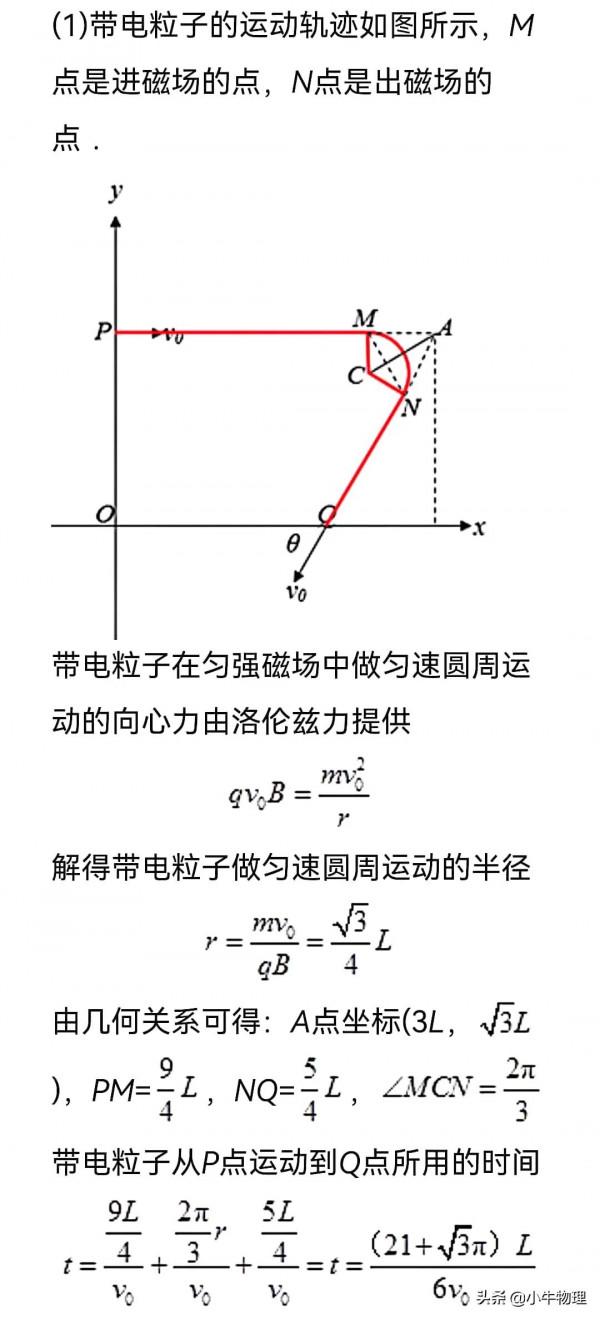
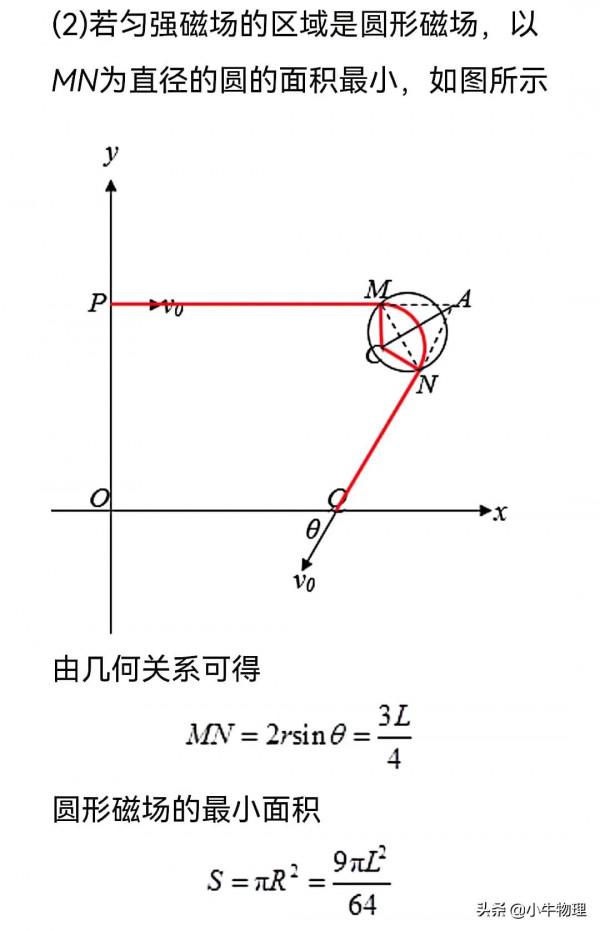
例題:如圖所示,在xOy平面第一象限內的某區域有垂直平面勻強磁場(沒畫出),一個質量為m、電荷量為q的電帶粒子。由y軸上的P點開始運動,初速度為v₀,方向沿x軸正方向;P到O的距離為√3L,後來,粒子經過x軸上的Q點,此時速度方向與x軸負方向的夾角為θ=60°,Q到O的距離為2L,磁場的磁感應強度B=4√3mv₀/
3qL。
(1)求帶電粒子從P點運動到Q點所用的時間;
(2)若勻強磁場的區域是圓形磁場,求圓形磁場的最小面積;
(3)若勻強磁場的區域是矩形,求矩形磁場的最小面積。
例題:如圖所示,在y軸右側存在磁感應強度大小為B,方向垂直紙面向裡的有界勻強磁場(圖中未畫出)。一束質量為m,電量為十q的粒子流,從座標原點沿x軸正向射入磁場,其速度大小介於2v₀與3v₀之間,經磁場偏轉後,所有粒子均沿y軸正方向射出磁場區域。不計粒子重力。求:
(1)粒子經過多長時間全部離開磁場;
(2)為防止粒子流汙染,在磁場外放置一塊板擋住粒子流,該板至少需要多寬;
(3)畫出滿足條件的磁場區域,並求出最小面積。
例題:在xOy平面內有許多電子(質量為m、電荷量為e),從座標原點O不斷地以相同的速率v₀沿不同方向射入第一象限,如圖所示。現加一個垂直於xOy平面向裡,磁感應強度為B的勻強磁場,要使這些電子穿過磁場區域後都能平行於x軸向x軸正向運動。求符合該條件磁場的最小面積。
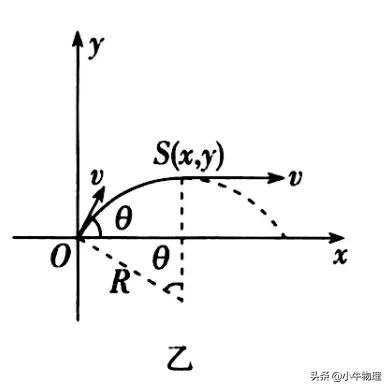
【解析】由題意可知,電子是以一定速度從原點沿任意方向射人第一象限的,先研究速度沿+y方向的電子,如圖甲所示,其在磁場中的運動軌跡是圓心在x軸上的A點、半徑為R=mv₀/qB的圓弧OCP。該電子沿圓弧OCP運動至最高點P時即朝x軸的正向,可見這段圓弧就是符合條件磁場區域的上邊界。當電子速度方向與x軸正向成角度θ時,作出軌跡圖如圖乙,當電子達到磁場邊界時,速度方向必須平行於x軸正方向,設邊界任一點的座標為S(x,y),由圖可知:
x=Rsinθ,y=R-Rcosθ
消去引數θ得:x²+(y-R)²=R²
可以看出隨著θ的變化,S的軌跡是圓心為(O,R),半徑為R的圓,即磁場區域的下邊界。
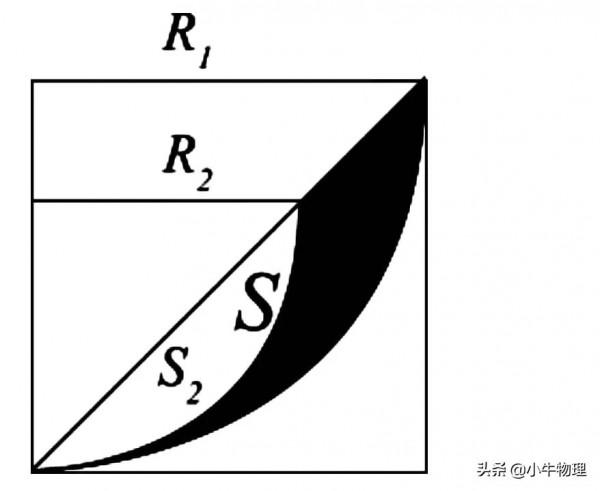
上下邊界就構成一個葉片形磁場區域。如圖甲所示。則符合條件的磁場最小面積為
例題:如圖所示,在平面直角座標系×oy中的第一象限記憶體在磁感應強度大小為B、方向垂直於座標平面向裡的有界圓形勻強磁場區域(圖中未畫出);在第二象限記憶體在沿×軸負方向的勻強電場,一粒子源固定在×軸上座標為(-L,O)的A點.粒子源沿y軸正方向釋放出速度大小為v的電子,電子恰好能透過y軸上座標為(0,2L)的C點,電子經過磁場偏轉後恰好垂直透過第一象限內與×軸正方向成15°角的射線ON(已知電子的質量為m,電荷量為e,不考慮粒子的重力和粒子之間的相互作用).求:
(1)勻強電場的電場強度E的大小;
(2)電子離開電場時的速度方向與y軸正方向的夾角θ;
(3)圓形磁場的最小半徑Rmin.
【分析】運動軌跡圖,先類平拋運動,後部分勻速圓周運動.
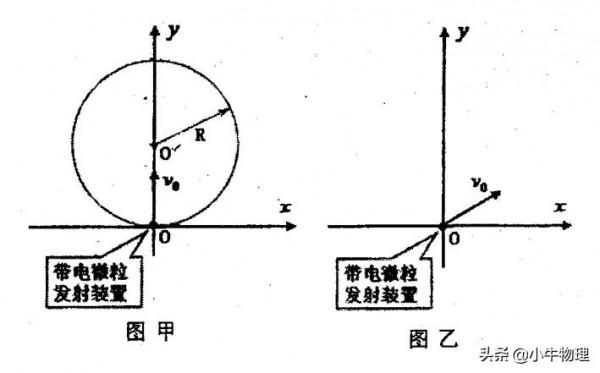
例題:如圖甲所示,x軸正方向水平向右,y軸正方向豎直向上。在xoy平面內有與y軸平行的勻強電場,在半徑為R的圓形區域內加有與xoy平面垂直的勻強磁場。在座標原點處放置一帶電微粒發射裝置,它可以連續不斷地發射具有相同質量m、電荷量q(q>0)和初速為v₀的帶電粒子。已知重力加速度大小為g。
(1)當帶電微粒發射裝置連續不斷地沿y軸正方向發射這種帶電微粒時,這些帶電微粒將沿圓形磁場區域的水平直徑方向離開磁場,並繼續沿ⅹ軸正方向運動。求電場強度和磁場強度的大小和方向。
(2)調節座標原點0處的帶電微粒發射裝置,使其在xoy平面內不斷地以相同的速率v₀沿不同方向將這種帶電微粒射入第Ⅰ象限,如圖乙所示。現要求這些帶電微粒最終都能平行於ⅹ軸正方向運動,則在保證勻強電場、勻強磁場的強度和方向不變的條件下,應如何改變勻強磁場的分佈區域?並求出符合條件的磁場區域的最小面積。
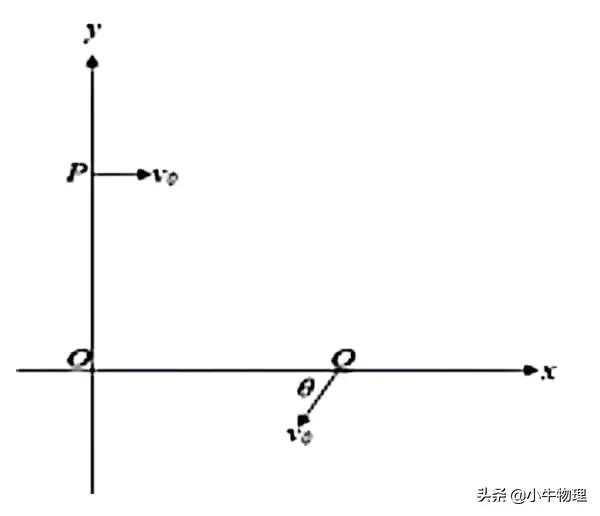
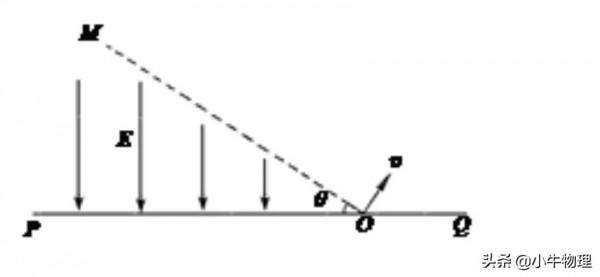
例題:如圖所示,虛線MO與水平線PQ相交於0點,夾角θ=30°,在MO左側存在電場強度為E、方向豎直向下的勻強電場;MO右側某個區域存在磁感應強度為B、垂直紙面向裡的勻強磁場,且O點在磁場的邊界上。現有大量質量為m、電量為+q的帶電粒子在紙面內以速度v(0<v≤E/B)垂直於MO從點射入磁場,所有粒子透過直線MO時,速度方向均平行於PQ向左。不計粒子的重力及粒子間的相互作用。
求:
(1)速度最大的粒子從O點運動至水平線PQ所需的時間;
(2)磁場區域的最小面積。