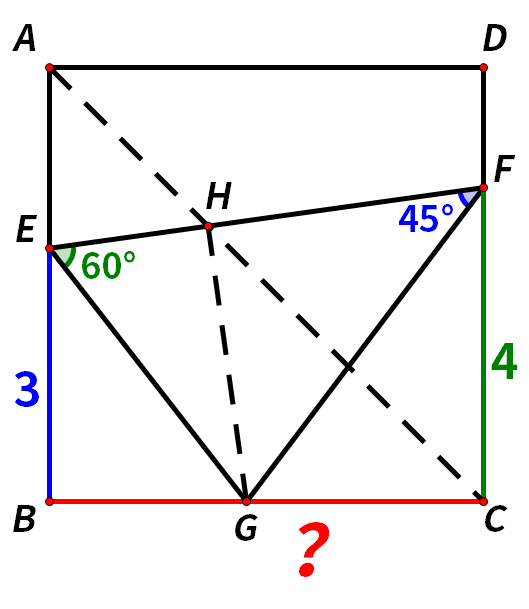
如圖,在正方形ABCD中,點E、F、G分別是AB、CD、BC邊上的點, BE=3, CF=4,∠FEG=60°,∠EFG=45°,求BC的長度。這道題怎麼做呢?
同學們看到60°還有45°,應該很容易想到構造直角三角形,但這裡不直接構造直角三角形,而是連線AC。這條輔助線有什麼用呢?
如圖所示,AC和EF交於點H,連線GH。
因為正方形的對角線平分正方形的內角,所以∠ACB=45°,即∠GCH=45°。
題目條件還告訴我們∠GFH=45°,∠GCH=∠GFH=45°。
根據這個條件,我們可以得到什麼樣的有效資訊呢?
由同弧所對的圓周角相等,可得點C、F、H、G四點共圓。
點C、F、H、G四點共圓,則四邊形CFHG對角互補,∠GCF=90°,所以∠GHF=90°。
三角形EHG和三角形FHG都是特殊的直角三角形。
假設EH的長度為x,根據30°、60°直角三角形的三邊關係,可得GH=√3x。
三角形FHG是等腰直角三角形,所以FH=GH=√3x。
而在三角形AEH和三角形CFH中,
由於AE平行CF,可得∠1=∠3,∠2=∠4,
所以三角形AEH和三角形CFH相似。
三角形AEH和三角形CFH相似,這兩個三角形對應邊成比例,
AE/CF=EH/FH,也就是 AE/4=x/√3x,解得AE=4√3/3。
所以BC=AB=AE+BE=4√3/3+3。
以上就是這道題的解法,除此之外你還有其他的方法嗎?可以在評論區留言~