開學已經三週左右了，大部分同學在下週或者十一以後就要迎接新學期的第一次月考了，所以，在同學們月考之前，小柒老師給同學們整理了七年級數學的月考提分資料，送給同學們，希望同學們在新學期的第一次月考取得好成績，為後面章節的學習打好基礎。

第一張 豐富的圖形世界

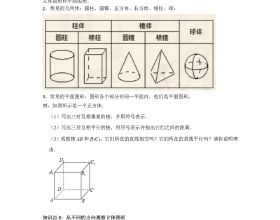
1. 生活中有各種各樣的立體圖形，常見的幾何體有圓柱、圓錐、正方體、長方體、稜柱、稜錐、球等。
2. 任何一個幾何體都由點、線、面構成，點無大小，線有曲直而無粗細，平面是無限延伸的，面有平面和曲面，面面相交得線，線線相交得點。點動成線，線動成面，面動成體。點、線、面、體都是幾何圖形。
3. 稜柱的有關定義：（1）稜：在稜柱中，任何相鄰的兩個面的交線叫側稜，稜柱的所有側稜長都相等。（2）面：稜柱的上、下底面相同。側面都是長方形，稜柱的名稱與底面多邊形的邊數有關。
4. 將一個圖形摺疊後能否變成稜柱，一要看有無兩個底面，二要看底面的形狀，三要看兩個底面的位置。
5. 一個正方體的表面沿某些稜剪開，可得到十多種不同的平面圖形，這些平面圖形經過摺疊後又能圍成一個正方體，圓柱和圓錐的側面展開圖分別是長方形和扇形。
6. 用一個平面去截一個正方體，若這個平面與這個正方體的幾個面相交，則截面就是幾邊形，依次得到三角形、四邊形、五邊形、六邊形。
7. 用一個平面去截一個幾何體，平面截的位置不同，所得的截面也不同，常見的截面是一個多邊形或圓。
8. 把從正面看到的圖形叫主檢視，從左面看到的圖形叫左檢視，從上面看到的圖叫俯檢視。
9. 學會畫三檢視。知道根據幾個小立方塊所搭建的幾何體的俯檢視畫出幾何體的主檢視和左檢視，以及根據主檢視和俯檢視搭幾何體，解題時注意觀察，確定主檢視\左檢視的列數，在確定每一列有幾層高。
10. 生活中的圖形離不開多邊形，它是由不在同一直線上的線段首尾相連組成的封閉圖形，從而一個n 邊形的一個頂點出發，分別連線這個頂點與其餘各頂點，可把這個多邊形分割成(n-2)個三角形。

第二章 有理數

1. 有理數：凡能寫成形式的數，都是有理數。正整數、0、負整數統稱整數；正分數、負分數統稱分數；整數和分數統稱有理數。注意：0既不是正數，也不是負數；-a不一定是負數，+a也不一定是正數。
2. 數軸：數軸是規定了原點、正方向、單位長度的一條直線。
3. 相反數：(1)只有符號不同的兩個數，我們說其中一個是另一個的相反數；0的相反數還是0；(2)相反數的和為0a+b=0a、b互為相反數。
4. 絕對值：(1)正數的絕對值是其本身，0的絕對值是0，負數的絕對值是它的相反數；注意：絕對值的意義是數軸上表示某數的點離開原點的距離。
5. 有理數比大小：（1）正數的絕對值越大，這個數越大；（2）正數永遠比0大，負數永遠比0小；（3）正數大於一切負數；（4）兩個負數比大小，絕對值大的反而小；（5）數軸上的兩個數，右邊的數總比左邊的數大；（6）大數-小數＞0，小數-大數＜0。
6. 互為倒數：乘積為1的兩個數互為倒數；注意：0沒有倒數；若a≠0，那麼的倒數是；若ab=1a、b互為倒數；若ab=-1a、b互為負倒數。
7. 有理數加法法則：（1）同號兩數相加，取相同的符號，並把絕對值相加；（2）異號兩數相加，取絕對值較大的符號，並用較大的絕對值減去較小的絕對值；（3）一個數與0相加，仍得這個數。
8. 有理數加法的運算律：（1）加法的交換律：a+b=b+a；（2）加法的結合律：（a+b）+c=a+（b+c）。
9. 有理數減法法則：減去一個數，等於加上這個數的相反數；即a-b=a+（-b）。
10. 有理數乘法法則：（1）兩數相乘，同號為正，異號為負，並把絕對值相乘；（2）任何數同零相乘都得零；（3）幾個數相乘，有一個因式為零，積為零；各個因式都不為零，積的符號由負因式的個數決定。
11. 有理數乘法的運算律：（1）乘法的交換律：ab=ba；（2）乘法的結合律：（ab）c=a（bc）；（3）乘法的分配律：a（b+c）=ab+ac。
12. 有理數除法法則：除以一個數等於乘以這個數的倒數；注意：零不能做除數。
13. 有理數乘方的法則：（1）正數的任何次冪都是正數；（2）負數的奇次冪是負數；負數的偶次冪是正數；注意：當n為正奇數時:(-a)n=-an或(a-b)n=-(b-a)n，當n為正偶數時，(-a)n=an或(a-b)n=(b-a)n。
14. 乘方的定義：（1）求相同因式積的運算，叫做乘方；（2）乘方中，相同的因式叫做底數，相同因式的個數叫做指數，乘方的結果叫做冪。
15. 科學記數法：把一個大於10的數記成a×10n的形式，其中a是整數數位只有一位的數，這種記數法叫科學記數法。
16. 近似數的精確位：一個近似數，四捨五入到那一位，就說這個近似數的精確到那一位。
17. 有效數字：從左邊第一個不為零的數字起，到精確的位數止，所有數字，都叫這個近似數的有效數字。
18. 混合運演算法則：先乘方，後乘除，最後加減。

第三章 整式加減

本節不是太難，我們抓住幾個“式”的概念，並且會判斷是否為同類項，同學們對概念要反覆推敲理解，然後多做一些練習題就能掌握。

1. 單項式：（1）都是數或字母的積的式子叫做單項式。（單獨的一個數或一個字母也是單項式。）如：2,2bc,3m,a,都是單項式。（2）單項式中的數字因數叫做這個單項式的係數。如：2ab中2是這個單項式的係數。（3）單項式係數應注意的問題：① 單項式表示數字與字母相乘時，通常把數字寫在前面；② 當單項式的係數是帶分數時，要把帶分數化成假分數；③ 當單項式的係數是1或-1時，“1”通常省略不寫；④ 圓周率π是常數；⑤ 單項式的係數應包括它前面的“正”、“負”符號。（4）一個單項式中，所有字母的指數的和叫做這個單項式的次數。如：xy2,這個單項式的次數是 3 次，而不是2次。（單獨的一個數的次數是0）
2. 多項式：（1）幾個單項的和叫做多項式。其中，每個單項式叫做多項式的項，不含字母的項叫做常數項。多項式的每一項都包含它前面的符號。（2）多項式裡次數最高項的次數，叫做這個多項式的次數。如：2a2+3b-5的次數是2.（3）單項式與多項式統稱整式。
3. 合併同類項：（1）所含字母相同，並且相同字母的指數也相同的項叫做同類項。幾個常數項也是同類項。 如：2a+3a-a+3a2中2a,3a,a是同類項，而2a,3a2則不是同類項。（2）把多項式裡的同類項合併成一項，叫做合併同類項。（3）、合併同類項法則：合併同類項後，所得項的係數是合併前各同類項的係數的和，且字母部分不變。
4. 去括號（1）去括號法則：① 如果括號外的因數是正數，去括號後括號內每一項的符號都不變。② 如果括號外的因數是負數，去括號後括號內每一項的符號都變。（2）去括號應注意：① 去括號應考慮括號內的每一項的符號，做的要變都變，要不變都不變；② 括號內原來有幾項，去掉括號後仍有幾項，同時括號前的符號也要去掉。