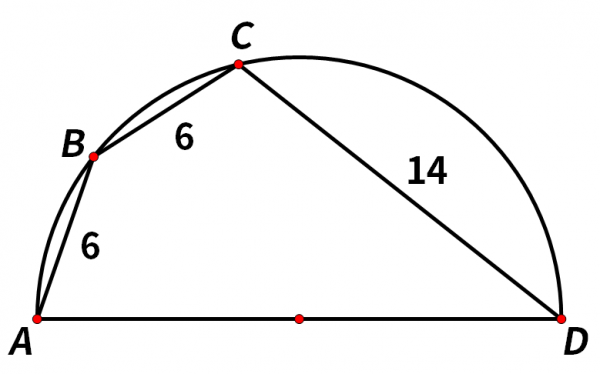
如圖,AB=BC=6,CD=14,求半圓直徑AD長。這道題怎麼做呢?
因為AB=BC,所以弧AB=弧BC。
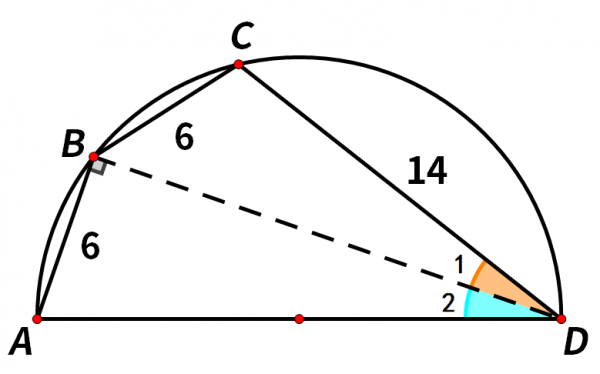
連線BD。
由同弧所對的圓周角相等,可得∠1=∠2。
∠ABD是直徑AD所對的圓周角,為90°。
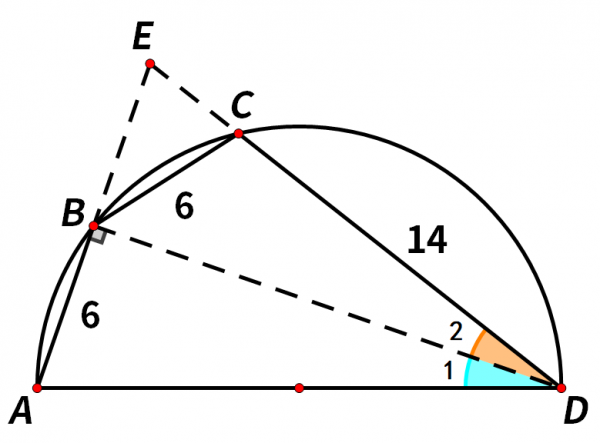
接著分別延長AB和DC,AB和DC的延長線交於點E。
在三角形ABD和三角形EBD中,
∠ABD=∠EBD=90°,
BD=BD(公共邊),
∠1=∠2,
由角邊角證全等可得,三角形ABD和三角形EBD全等。
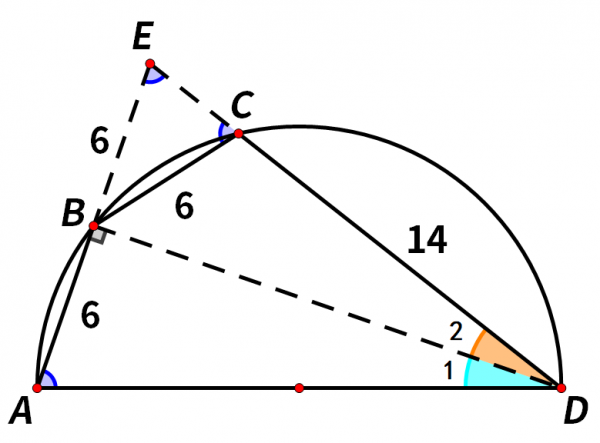
三角形ABD和三角形EBD全等,∠DAB=∠E,EB=AB=6,AD=ED。
而AB=BC=6,等量代換,EB=BC。
EB=BC,等邊對等角,∠E=∠BCE。
接下來我們看到三角形BEC和三角形DAE,
∠BEC=∠DAE,
∠BCE=∠DEA,
三角形BEC和三角形DAE相似。
三角形BEC和三角形DAE相似,它們的對應邊成比例,
BC/DE=CE/EA,即6/(14+CE)=CE/12,解得CE=4。
AD=ED=CE+CD=4+14=18。
以上就是這道題的解法,除此之外,你還有其他方法嗎?可以在評論區留言~