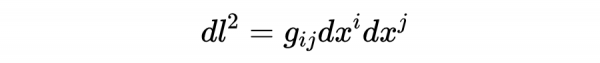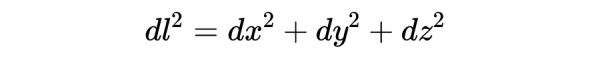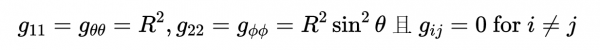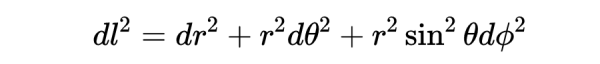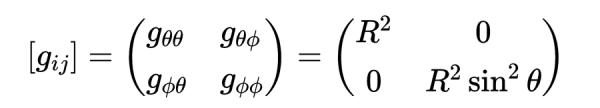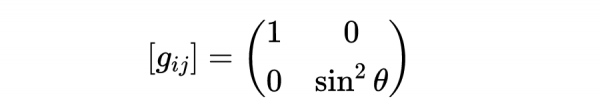有人告訴我,我在書中加入的每一個方程式都會使銷售量減半——霍金
牛頓引力與狹義相對論是不相容的,因為在牛頓的理論中,引力在任何距離上都是瞬時作用的。狹義相對論不允許這一點,而是強加了一個自然的速度極限——光速。為了調和相對論和引力,我們現在需要從狹義相對論的(平坦的))=閔可夫斯基空間移動到廣義相對論的彎曲時空。愛因斯坦在形成廣義相對論時的偉大見解是:
- 物質和能量會扭曲時空
- 時空可以用一種被稱為偽黎曼流形的數學結構來建模。
因此,廣義相對論中的引力不再被視為一種力,而是時空幾何的一種屬性。
為了理解彎曲空間的幾何概念,米斯納等人以一隻螞蟻在蘋果皮上爬行為例。螞蟻決定儘可能走得筆直,於是仔細地量了量自己的步子,使其長度相等。如果螞蟻冒險太靠近蘋果的頂部,即使它試圖走直線,也會發現自己被拉進蘋果頂部的凹窩裡。一個有想象力的人可能會說,有一個力把它吸引到蘋果的凹窩裡。當然不存在力。螞蟻的路徑不是由外力決定的,而是由蘋果表面的曲率——幾何形狀——決定的。米斯納想象一個物理系的學生看著螞蟻的行進,然後拿起一把刀,小心地把螞蟻走過的蘋果皮的痕跡切下,放在他的書上。在觀察到軌道“像鐳射束一樣直”之後……這隻螞蟻沒有比這更“經濟”的路徑來“覆蓋”這10釐米的果皮了”,這隻螞蟻的路徑形成了“一條美麗的測地線”。
狹義相對論中的(平坦的)閔可夫斯基空間存在於深空,遠離任何引力場的影響。在平坦的時空中,自由粒子沿直線運動。在大質量物體附近的時空是彎曲的。包括光在內的自由粒子將不會沿直線運動,而是沿著彎曲時空的幾何形狀所決定的“可能最直”的路徑運動,就像螞蟻沿著蘋果表面所決定的可能最直的路徑運動一樣。
這些路徑被稱為測地線,我們可以粗略地定義為彎曲空間中兩點之間的最直或最短距離。例如,球面上的測地線是大圓的一部分(與球面直徑相同,圓心為球面中心點,如赤道,或任何經度線的圓)。如果時空的數學結構是已知的——即它是如何彎曲的——那麼運動的粒子(以及行星和恆星)的測地線就可以透過觀測來計算和測試。
為了在數學上描述彎曲空間,我們使用流形的概念,廣義地定義為區域性平坦的光滑彎曲空間。例如,一個圓是一個一維流形:使它足夠大,小段看起來像一條直線。球體的表面是二維流形:它的小塊看起來是平的。時空,一種四維流形,在區域性也是平坦的,並且在足夠小的區域內,就會簡化為狹義相對論中的時空。
我們說流形是n維的,因為流形上的每個點都可以用n維或座標來表示。線和圓是一維流形:它們上的任何點都可以用一個座標來描述(例如,線沿直線的距離,圓的極角)。平面是一個二維流形,就像球體的表面一樣:表面上的任何點都可以使用球面極座標θ和φ來描述。正如我們所看到的,時空是四維的,需要一個時間座標加上三個空間座標來確定時空中的一個點。
並不是所有的空間結構都是流形。從平面上顯現出來的一維直線不是流形,兩個錐尖之間彼此重疊也不是。因為這些物體不是區域性的歐幾里得,所以它們不屬於流形。
黎曼流形和度規
為了能夠模擬廣義相對論的時空,流形還必須具有這兩個附加屬性:
- 它一定是可微的。當我們看張量的變換性質時,這將變得非常清楚,因為它包含了大量的偏導數。
- 它必須被賦予一個對稱度規張量,在狹義相對論中,它定義了流形上附近點的間隔。度規的形式將透過流形改變,這取決於該區域的時空如何彎曲。例如,在遠離物質和能量影響的深空,時空將近似於狹義相對論中的閔可夫斯基空間。在一個不旋轉的黑洞附近,將近似史瓦西度規。度規完全定義了流形的曲率,因此在相對論中具有根本的重要性。
一個可微的和具有對稱度規張量的流形被稱為黎曼流形。黎曼發現度規包含了我們描述流形曲率所需要的所有資訊。如果我們知道度規,我們就知道空間。這就是為什麼度規對廣義相對論至關重要。
n維黎曼流形的線元為:
其中
是度規,
是座標微分,它意味著度規決定了線元的係數。當我們遇到笛卡爾座標中的三維歐幾里德線元素時,我們看到了一個簡單的例子
歐幾里得度規是:
在上面的歐幾里德線元中有1 × dx^2, 1 × dy^2和1 × dz^2。我們也看到過笛卡爾座標下的閔可夫斯基線素
閔可夫斯基度規是
上述閔可夫斯基線元中有1 × c^2dt^2、-1 × dx^2、-1 × dy^2、-1 × dz^2。
順便說一下,我們知道這些度規描述了平坦空間,因為它們的度規係數是±1。然而,如果我們選擇一個奇怪的座標系,我們很可能最終得到一個複雜的度規,其係數不等於±1。
我們如何判斷度規是否定義了平坦空間?答案是黎曼曲率張量,這是確定流形是平的還是彎曲的絕對苛刻的測試。如果黎曼曲率張量對於特定空間中的所有點都是零那麼這個空間就是平坦的。如果張量在某一點不等於零,那麼空間在那一點是彎曲的。
當我們想到圓或球面時,我們認為它們存在於日常的歐幾里德空間中。我們可以在一張座標紙上畫一個圓,或者把一個球放在桌子上。然後我們可以把圓的曲率和畫在座標紙上的直線相比較,或者把球體的圓度和桌子的平坦度相比較。
在數學術語中,我們說圓和球表現出外部曲率,因為它們的曲率與一個更高維度的外部空間有關——紙張是二維,桌子是三維。然而,並不是所有的流形都可以被認為以這種方式嵌入到外部空間中。我們常常需要根據流形本身的條件來研究它,也就是說,不需要參考更高維度的空間。這種型別的曲率稱為本徵曲率。
我們透過直接檢查它們來理解本質上彎曲的流形,使用從度規衍生出來的度量和數學工具來分析它們的內部結構。在廣義相對論中,我們只對時空的固有曲率感興趣。
把一個捲起來的圓柱體放在桌子上,我們可以看到它與桌子的平面相比具有外部曲率。然而,本質上,圓柱體是平的——畫在其表面上的三角形內角之和等於180°。這並不奇怪,因為我們可以展開圓柱體,最後得到一張平坦的紙。
和圓柱體一樣,桌面上的球有一個外曲面。然而,球的表面本質上也是彎曲的。在球面上,經度線在赤道上平行,但在兩極相交。另外,球面上三角形的內角可以都等於90度。與圓柱體不同的是,球面不能在不變形的情況下被平坦化,地圖繪製者在試圖將地球表面投影到平面地圖上時發現了這一點。
球的表明
球面是最簡單的二維流形之一。
之前,我們遇到了用球座標描述歐幾里德三維空間的線元和度規。線元為
如果我們將極座標R設為某個常數r,我們就失去了dr項,並且定義了球面的線元:
它使用兩個極座標(θ, ϕ)描述一個二維表面。我們知道,使用座標(θ, φ)的這個表面的度規是
其中
逆度規是
對於單位半徑球(R = 1),這些度規變成
時空流形是相對論的舞臺。下面我們將看到在舞臺上表演的主要演員。這些數學物件被稱為標量、逆變向量、1-形式(對偶向量、協變向量)和張量。