奧珀曼猜想(Oppermann's conjecture)
關於平方數附近的質數,存在著名但仍未被證明的奧珀曼猜想(Oppermann's conjecture)。該猜想指出:
- 對於每個整數 x > 1,x(x - 1) 和 x^2 之間至少有一個素數;
- x^2 和 x(x+1) 之間至少有另一個素數。
也可以等效地表述為,
π(x^2 − x) < π(x^2) < π(x^2 + x) for any integer x > 1
這裡π(x)為質數計數函式,表示所有不超過x的質數數目。
平方後繼質數不等式 NextPrime-Square-Inequality
三之五年前,我在Sagemath中進行實驗,發現了一個新的不等式,
NextPrime-Square-Inequality:
next_prime(n^2) - n^2 <= 1+euler_phi(n)
尤拉函式euler_phi(n)是小於等於n的正整數中與n互質的數的數目, 一般表示為φ(n)。當p為質數時,φ(p)=p-1;當n為合數時,φ(n)會比n小很多。因此,我發現的NextPrime-Square-Inequality是對Oppermann's conjecture的一次改進。
下面時我進行這次數學實驗的部分sagemath程式碼:
def next_prime_delta(x):
return next_prime(x)-x
def previous_prime_delta(x):
return previous_prime(x)-x
[(n,euler_phi(n),next_prime_delta(n^2)) for n in range(1,50)]輸出:
[(1, 1, 1),
(2, 1, 1),
(3, 2, 2),
(4, 2, 1),
(5, 4, 4),
(6, 2, 1),
(7, 6, 4),
(8, 4, 3),
(9, 6, 2),
(10, 4, 1),
(11, 10, 6),
(12, 4, 5),
(13, 12, 4),
(14, 6, 1),
(15, 8, 2),
(16, 8, 1),
(17, 16, 4),
(18, 6, 7),
(19, 18, 6),
(20, 8, 1),
(21, 12, 2),
(22, 10, 3),
(23, 22, 12),
(24, 8, 1),
(25, 20, 6),
(26, 12, 1),
(27, 18, 4),
(28, 12, 3),
(29, 28, 12),
(30, 8, 7),
(31, 30, 6),
(32, 16, 7),
(33, 20, 2),
(34, 16, 7),
(35, 24, 4),
(36, 12, 1),
(37, 36, 4),
(38, 18, 3),
(39, 24, 2),
(40, 16, 1),
(41, 40, 12),
(42, 12, 13),
(43, 42, 12),
(44, 20, 13),
(45, 24, 2),
(46, 22, 13),
(47, 46, 4),
(48, 16, 5),
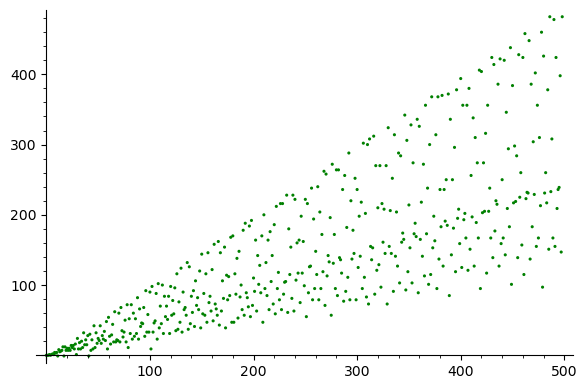
(49, 42, 10)]list_plot([euler_phi(n)-next_prime_delta(n^2) for n in range(1,500)], color='green', pointsize=5)
朝著證明Oppermann's conjecture努力
試圖證明n^2 和 n(n+1) 之間必有素數時,我嘗試為
{n^2+1, n^2+2, n^2+1,...,next_prime(n^2)-1}
分配各不相同的真因子,但對某些n,並不能做到這些真因子都小於n。
這並不遺憾,現在,將n^2後繼質數與尤拉函式φ(n)相關聯,也許從中可以找到證明Oppermann's conjecture的靈感線索!