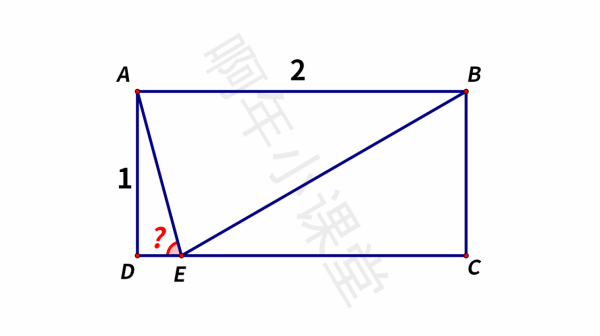
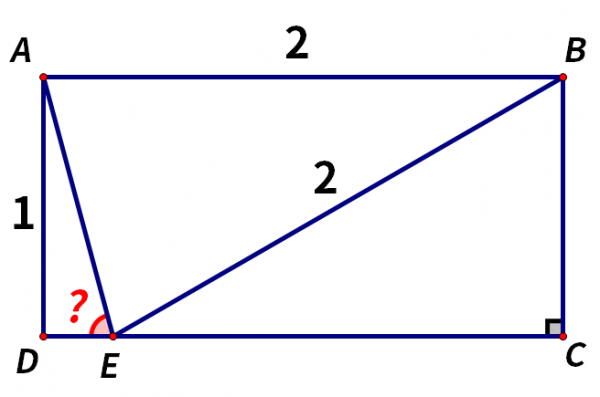
如圖,在矩形ABCD中,AB = 2,AD = 1,點E在邊DC上,且AE平分∠DEB,求∠AED的度數。這題怎麼做呢?
這道題不難,但還是有不少同學不會,我們先看一下根據題目條件可以得到什麼有限資訊。
根據AE平分∠DEB可得,∠AED=∠AEB,
而由四邊形ABCD是矩形可得AB∥DC,BC=AD=1,∠C=90°。
AB∥DC,
兩直線平行,內錯角相等,
所以∠AED=∠BAE。
∠AED=∠AEB,∠AED=∠BAE,
由等量代換,可得∠AEB=∠BAE,
所以三角形ABE是等腰三角形,
BE=AB=2。
接下來我們看到三角形BCE。
在三角形BCE中,∠C=90°,BE=2,BC=1,
所以三角形BCE是30°、60°直角三角形,
∠BEC=30°,
∠DEB=180°-∠BEC=180°-30°=150°,
又因為AE平分∠DEB,所以∠AED=∠AEB=150°÷2=75°。
以上就是這道題的解法。