「漫步計算機系統」之資料結構與演算法（26）：圖的最小生成樹

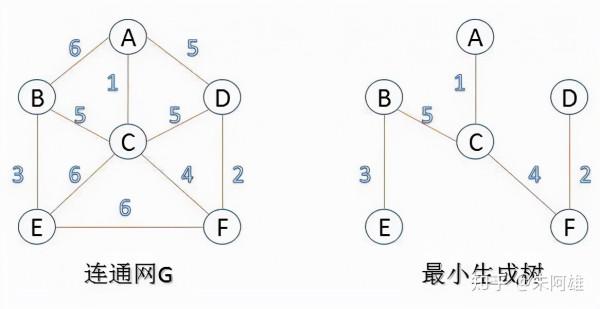
連通圖：在無向圖中，每對頂點之間都有路徑可達；

強連通圖：在有向圖中，每對頂點之間都有路徑可達；

連通網：在有向圖中，若連線兩個頂點之間的邊用一個數表示，這個數稱為權，權具有特定的意義，代表這條邊的代價；

生成樹：一個連通圖，它包含所有的n個頂點，且這個圖中有n-1條邊，一個生成樹有且僅有n個頂點和n-1條邊，若增加一條邊，則構成環，若減少一條邊，則不是連通圖；

最小生成樹：在連通網的所有生成樹中，權的和最小的生成樹。

Kruskal演算法

初始最小生成樹邊數為0，每次迭代找權最小的邊加入最小生成樹邊的集合中，但不能形成環；

1. 將圖中邊按照權從小到大排序；
2. 從小到大選擇邊，且選擇的邊不構成環，則加入最小生成樹邊的集合，若構成環，則繼續選擇下一條稍大且不構成環的邊加入集合；
3. 重複2，直到集合中邊的數目為n-1。

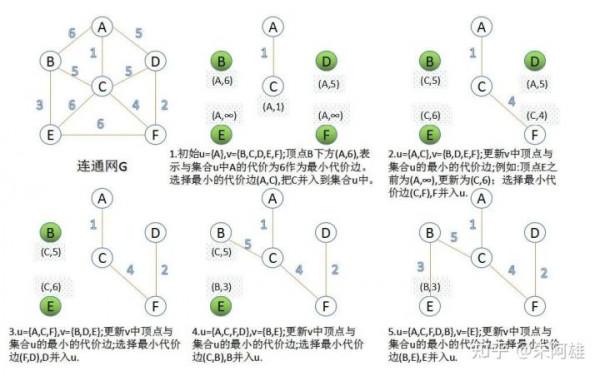
Prim演算法

首先從權最小的邊開始，選擇這條邊的一個頂點加入最小生成樹頂點集合，一直到所有頂點都加入集合，且不構成環；

1. 設圖中所有頂點集合為V，初始頂點集合u={s}，v=V-u；
2. 從u和v中找兩個頂點u0和v0，兩個頂點間邊的權最小，將v0加入集合u中；
3. 重複2，知道集合u的大小為n。

注：凡屬於本公眾號內容，未經允許不得私自轉載，否則將依法追究侵權責任。