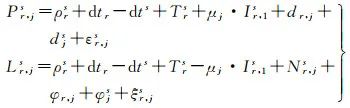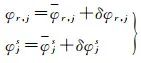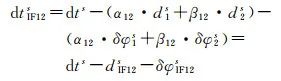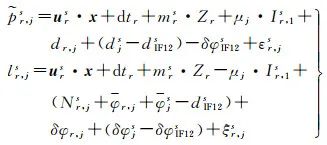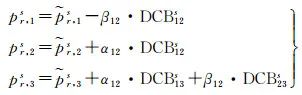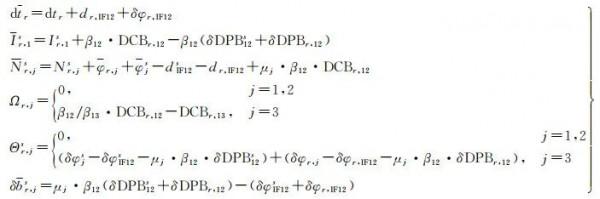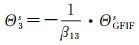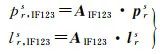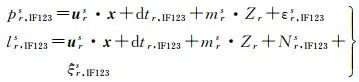
本文內容來源於《測繪學報》2021年第1期，審圖號GS（2021）17號。

GPS/BDS/Galileo三頻精密單點定位模型及效能分析

周鋒¹

, 徐天河²

1. 山東科技大學測繪科學與工程學院, 山東 青島 266590;

2. 山東大學空間科學研究院, 山東 威海 264209

基金專案：國家自然科學基金（41904027；41904011）；中國博士後科學基金（2020M673669）；大地測量與地球動力學國家重點實驗室開放研究基金（SKLGED2020-3-2-E）；山東省自然科學基金（ZR2019QD003）

摘要：在精細考慮偽距和載波相位硬體偏差時變特性的基礎上，匯出了更為嚴謹的非差非組合觀測方程，並給出了非組合模式下兩類GNSS偏差的數學表達形式。基於此，本文詳細研究了3種常用的三頻精密單點定位（PPP），即無電離層兩兩組合IF1213、單個無電離層組合IF123與非組合UC123函式模型的獨立引數化方法，系統分析了3種PPP模型的相互關係以及GPS/BDS/Galileo三頻靜、動態PPP定位效能。結果表明，靜態PPP收斂後定位精度水平方向優於1.0 cm，高程優於1.5 cm；動態PPP水平方向優於2.0 cm，高程優於5.0 cm；三頻PPP的定位效能與雙頻PPP基本相當。

關鍵詞：GPS/BDS/Galileo精密單點定位GNSS偏差三頻觀測值定位效能

Modeling and assessment of GPS/BDS/Galileo triple-frequency precise point positioning

引文格式：周鋒, 徐天河. GPS/BDS/Galileo三頻精密單點定位模型及效能分析[J]. 測繪學報，2021，50(1)：61-70. DOI: 10.11947/j.AGCS.2021.20200146.

閱讀全文：http://xb.sinomaps.com/article/2021/1001-1595/2021-1-61.htm

全文概述

精密單點定位(precise point positioning，PPP)是指利用外部提供的高精度衛星軌道和鐘差產品，在綜合考慮各項誤差精確改正的基礎上，採用合理的引數估計策略(如最小二乘或Kalman濾波等)，利用單臺GNSS接收機的載波相位和偽距觀測值實現全球高精度絕對定位(一般可達分米至毫米級)的一項技術^[1]。PPP技術自20世紀90年代被提出並實現後^[2-3]，經過將近30年的快速發展，基本理論和工程實踐已日趨成熟，目前已廣泛應用於廣域精密定位、低軌衛星定軌、水汽反演與電離層監測、地震與海嘯的監測和預警、時間傳遞等領域^[4-7]。

得益於全球分佈的大地型GNSS接收機，PPP技術自問世以來，大多采用雙頻PPP模型，已有學者從模糊度固定角度詳細論述了不同雙頻PPP模型的相互關係^[8]。隨著美國GPS現代化、我國BDS和歐盟Galileo導航衛星系統的迅速建設，越來越多的導航衛星開始播發三頻訊號，三頻PPP的研究和應用也越來越廣泛與深入^[9]。基於BDS三頻觀測值，文獻[10-11]系統研究了3種BDS三頻PPP觀測模型及其定位效能，即基於B1/B2和B1/B3無電離層組合觀測值、基於單個無電離層組合觀測值及基於非差非組合觀測值的三頻PPP模型。文獻[12]基於GPS三頻觀測值對比分析了不同三頻PPP模型的定位效能。不同研究結果表明，三頻PPP與雙頻PPP在收斂效能和定位精度等效能指標上基本相當。針對城市複雜環境下(如訊號遮擋、衰減和多徑頻繁發生)的智慧交通、自動駕駛等對高精度動態定位的需求，文獻[13]充分利用三頻多系統GNSS資料，提出單曆元寬巷模糊度固定PPP方法，並與傳統雙頻PPP和廣域偽距增強精密定位方法進行對比分析。結果表明，在干擾因素多的城市複雜環境中，單曆元寬巷模糊度固定PPP定位效果更好。可以看出，三頻觀測值的加入，不僅可以提升PPP模糊度固定效率，還將提升複雜場景下PPP定位的可用性及可靠性。

近年來，已有大量研究針對三頻PPP模型與定位效能進行了廣泛的驗證與分析，但鮮有文獻對三頻PPP模型間進行系統性的研究與比較，而且對三頻PPP模型中GNSS偏差的產生機制及數學表達缺乏深入探討。從原始非差非組合觀測方程出發，在精細考慮偽距和載波相位硬體偏差的基礎上，本文詳細地研究了3種常用的三頻PPP函式模型的獨立引數化方法，系統分析了3種PPP模型的相互關係，並給出了非組合模式下兩類GNSS偏差(如接收機偽距頻間偏差和載波相位頻間衛星鐘偏差)嚴格的數學表達形式。本文利用GPS/BDS/Galileo三頻PPP算例，分析驗證了理論的正確性及不同模型的定位效能。

1 三頻PPP觀測模型

本節給出三頻PPP的觀測模型，包括函式模型及其對應的隨機模型。為簡單起見，利用L1、L2和L3分別表示GPS L1、L2和L5頻率，BDS B1、B2和B3頻率及Galileo E1、E5a和E5b頻率。具體見表 1。

表 1 GPS/BDS/Galileo衛星系統及其對應的頻率

Tab. 1 Selected frequencies of GPS/BDS/Galileo

1.1 函式模型

從非差非組合GNSS原始觀測方程出發，建立三頻PPP函式模型，並對不同模型的異同點進行了細緻研究。

1.1.1 原始觀測方程

一般地，非差非組合GNSS偽距和載波相位觀測方程可表示如下

(1)

式中，s、r和j(j=1, 2, 3)分別代表衛星、接收機和載波頻率號；Pr,js和Lr,js分別為偽距和載波相位觀測值；ρ_r^s表示衛星到接收機的幾何距離；dt_r和dt^s分別為接收機和衛星鐘差；T_r^s為視線方向對流層斜延遲；Ir, 1s為第一頻率上的電離層斜延遲；μ_j=f₁²/f_j²為電離層放大因子，f為載波頻率；Nr,js為載波相位模糊度；dr,j和d_j^s分別表示接收機和衛星偽距硬體偏差，相應地，φr,j和φ_j^s分別為接收機和衛星相位硬體偏差；εr,js和ξr,js分別為偽距和載波相位觀測值對應的觀測噪聲和多路徑效應等非建模綜合誤差。式中各變數的單位均為m。需要注意的是，式(1)中不包括衛星和接收機天線相位中心改正、相對論效應、潮汐負荷形變(固體潮、極潮和海潮)、薩奈克效應(Sagnac effect)、衛星天線相位纏繞(僅對載波觀測值)等改正，這些已事先透過模型改正^[14]。

對於偽距和相位硬體偏差，通常認為偽距硬體偏差比較穩定，一天內變化較小^[15-16]。而相位硬體偏差具有明顯的時變特性，可將相位硬體偏差分解為常數部分和時變部分^[17-18]，即

(2)

式中，φr,j和φ_j^s分別表示接收機和衛星相位硬體偏差常數部分，相應地，δφr,j和δφ_j^s分別對應其時變部分。由於常數特性，可以認為φr,j和φ_j^s完全被模糊度引數吸收，即Nr,js=Nr,js+φr,j+φ_j^s。

為簡便起見，定義以下變數

(3)

式中，f_i和f_j為不同的載波相位頻率(i,j=1, 2, 3;i≠j)；α_ij和β_ij為無電離層組合係數因子；DCB_ij^s和DCBr,ij為衛星和接收機差分碼偏差；δDPB_ij^s和δDPBr,ij為衛星和接收機差分時變相位偏差；dIFijs和dr, IFij分別表示衛星和接收機偽距硬體偏差的無電離層組合；δφIFijs和δφr, IFij分別為衛星和接收機時變相位偏差的無電離層組合。

目前GNSS精密衛星鐘差產品一般是基於L1/L2雙頻(如GPS L1/L2、BDS B1/B2與Galileo E1/E5a)無電離層組合偽距和載波觀測值計算得到^[19]。因此，精密衛星鐘差包含了雙頻偽距硬體偏差與相位硬體偏差時變部分的線性組合，即

(4)

引入精密衛星軌道和鐘差改正，將式(4)代入式(1)併線性化得

(5)

式中，

和lr,js分別表示偽距和載波相位觀測值減去計算值(observed minus computed，OMC)；u_r^s表示接收機與衛星連線的方向餘弦；x為三維座標改正數；Z_r為測站天頂對流層溼延遲；m_r^s為對應的溼投影函式。

式(5)中的偽距偏差項d_j^s－d_IF12s在不同頻率偽距觀測值上可以表達為差分碼偏差DCB形式，PPP使用者可選擇改正或不改正此項。若從觀測方程中改正此項，則

(6)

顧及式(6)，則式(5)可進一步寫為

(7)

式中

(8)

式中，dt_r、Ir, 1s和Nr,js分別表示重新引數化後的接收機鐘差、電離層延遲和載波相位模糊度引數；Ωr,j表示非組合觀測量中接收機端偽距頻間偏差(inter-frequency bias，IFB)；Θr,js表示非組合觀測量中頻間鍾偏差(inter-frequency clock bias，IFCB)；δbr,js為未引數化的衛星和接收機相位硬體偏差時變部分的綜合，將進入偽距觀測值殘差，相比偽距觀測值噪聲，δbr,js的量級相對較小，可忽略其影響。

可以看出，式(7)是更為嚴密的非差非組合函式模型，可作為單、雙和三頻甚至多頻PPP模型的基本模型。在當前基於雙頻無電離層組合觀測值的精密衛星鐘差估計規則的前提下，單、雙頻PPP無需考慮Ωr,j和Θr,js，而三頻PPP需改正掉Θr,js，此外還需將Ωr,j引數化。

IFCB估計一般基於經典的無幾何距離無電離層(geometry-free and ionospheric-free，GFIF)組合觀測量計算得到^{[17, 20]}。文獻[21-22]論證了IFCB與衛星有關，而與接收機無關，並給出了將GFIF組合觀測量估計的IFCB轉化為非組合觀測值下的IFCB的轉換關係，即

(9)

式中，Θ_GFIFs表示基於GFIF組合觀測量估計的IFCB。

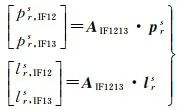
接著，在式(7)的基礎上，建立3種常用的三頻PPP函式模型。為簡便起見，用IF1213-PPP、IF123-PPP和UC123-PPP分別表示基於L1/L2和L1/L3兩個無電離層組合觀測值、基於單個無電離層組合觀測值及基於非差非組合觀測值的三頻PPP模型。首先給出三頻偽距和載波相位OMC觀測向量，即

(10)

1.1.2 IF1213-PPP模型

IF1213-PPP由兩個不同的無電離層組合觀測量得到，可表達為

(11)

式中，設計矩陣

。

為使觀測方程中接收機鐘差引數保持一致，將式(11)展開並改寫為

(12)

式中

(13)

式中，Ωr, IF1213為IF1213組合下的接收機IFB。

可以得出，IF1213-PPP的待估引數向量為

(14)

式中，

，n為可觀測到的衛星數。

1.1.3 IF123-PPP模型

IF123-PPP利用三頻觀測值直接組成無電離層組合觀測量，即

(15)

式中，設計矩陣A_IF123=[e₁e₂e₃]，e₁、e₂和e₃為線性組合係數，且滿足以下關係式

(16)

式(16)採用了最小觀測值噪聲作為約束條件來唯一確定組合係數，其最優估值可透過解拉格朗日方程R(e₁,e₂,e₃,κ₁,κ₂)=e₁²+e₂²+e₃²+κ₁(e₁+e₂+e₃－1)+κ₂(e₁+e₂μ₂+e₃μ₃)=min得到，首先獲得R對於每一個估值的偏導數，使偏導數為0來獲得組合係數，即

(17)

將式(15)展開，得

(18)

式中

(19)

相應地，IF123-PPP的待估引數向量為

(20)

式中，

。

1.1.4 UC123-PPP模型

UC123-PPP在不同頻率觀測值之間不作線性組合，而是直接利用原始偽距和載波觀測值，即

(21)

式中，設計矩陣A_UC123=diag(1, 1, 1)。其中，diag(•)表示對角陣。

結合式(7)和式(8)，將式(21)進一步展開為

(22)

相應地，UC123-PPP的待估引數向量為

(23)

式中，

。

1.1.5 三頻PPP模型間的聯絡

在觀測方程層面，IF1213-PPP、IF123-PPP和UC123-PPP都是基於三頻原始觀測值的線性組合形成，設計矩陣(或線性組合係數陣)分別對應A_IF1213、A_IF123和A_UC123。不同的是，前兩者需對不同頻率觀測值進行線性組合以消除電離層延遲影響，而UC123-PPP在不同頻率觀測值之間無須做線性組合。

在待估引數層面，3個模型對應相同的位置引數和對流層溼延遲引數，而估計的載波相位模糊度各不相同；不同於IF123-PPP，IF1213-PPP和UC123-PPP估計相同的接收機鐘差引數。此外，IF1213-PPP和UC123-PPP需分別估計一個接收機偽距IFB引數，且兩者存在下述轉換關係

(24)

1.2 隨機模型

假設不同頻率觀測值之間相互獨立，且不同頻率偽距或載波相位觀測值噪聲相同，即滿足σP1=σP2=σP3=σ_P和σL1=σL2=σL3=σ_L。非組合三頻觀測值對應的方差-協方差陣Σ_UC可以表示為

(25)

式中，σP|L=a/sin(E)，其中a為觀測值噪聲，對於載波觀測值，一般經驗地取為0.003 m；而對於偽距觀測值，一般取0.3 m；E為衛星高度角。

根據誤差傳播定律，IF1213-PPP、IF123-PPP和UC123-PPP對應的方差-協方差陣為

(26)

式中，Σ_IF1213、Σ_IF123和Σ_UC123分別為IF1213-PPP、IF123-PPP和UC123-PPP模型的觀測值方差-協方差陣。

2 試驗結果分析

2.1 資料介紹及處理策略

為驗證GPS/BDS/Galileo三頻PPP定位效能，選取均勻分佈的25個MGEX測站於2019年7月的觀測資料(取樣間隔為30 s)進行資料處理，測站地理分佈見圖 1，測站所處經緯度、配備的接收機型別和天線型別資訊見表 2。可以看出，所選測站的接收機型別有4種，分別是SEPT POLARX5、JAVAD TRE_3 DELTA、TRIMBLE ALLOY和TRIMBLE NETR9，其中配備TRIMBLE NETR9和SEPT POLARX5接收機的測站佔比分別為56%和32%。此外，所選測站均具備跟蹤GPS/BDS/Galileo三頻訊號的能力且滿足每個曆元跟蹤到每個衛星系統的衛星數均大於或等於4顆。表 3給出了可以播發三頻觀測值的GPS、BDS和Galileo衛星情況，其中包括部分GPS衛星(12顆)以及全部的BDS(15顆)和Galileo衛星(24顆)。

圖 1 選取的25個MGEX測站分佈Fig. 1 Geographical distribution of the selected 25 MGEX tracking stations

圖選項

表 2 所選MGEX測站基本資訊

Tab. 2 Information of the selected MGEX tracking stations

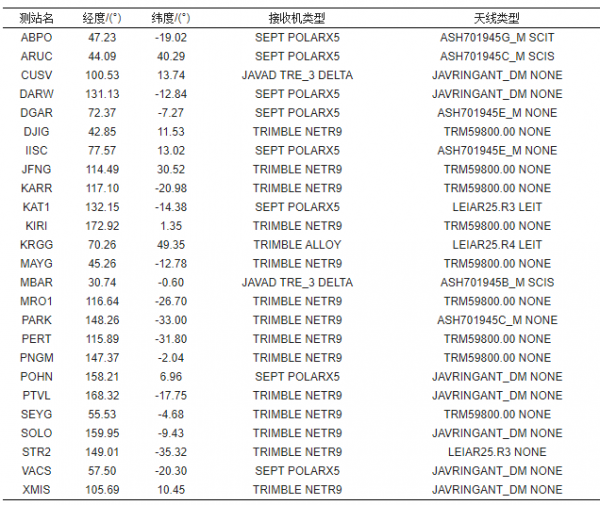
表 3 具備三頻訊號播發能力的GPS/BDS/Galileo衛星情況

Tab. 3 Information of GPS/BDS/Galileo satellites tracking triple-frequency signals

本文GPS/BDS/Galileo三頻PPP解算採用的衛星軌道和鐘差產品由德國地學研究中心(GFZ)提供。試驗採用靜態和仿動態PPP兩種解算模式，靜態PPP解算的座標引數為常數估計，而動態PPP的座標引數為白噪聲估計，本文的PPP解算均在開源GAMP軟體^[23]上完成。此外，接收機鐘差引數為白噪聲估計，而接收機IFB採用常數估計^[10]；以GPS對應的接收機鐘差為參考，其他系統(如BDS和Galileo)估計的是該系統對應的接收機鐘差與GPS對應的接收機鐘差的差值，即系統間偏差(inter-system bias，ISB)，採用白噪聲估計^[24]。對流層溼延遲採用隨機遊走過程估計，譜密度取

；對於UC123-PPP，電離層延遲引數為白噪聲估計^[10]；載波相位模糊度不固定，保持浮點解狀態，在連續弧段內為常數，在發生周跳時重新初始化。由於IGS尚未提供BDS和Galileo系統對應的接收機天線相位中心改正，因此利用GPS L1和L2頻率的接收機相位中心改正代替BDS B1和B2與Galileo的E1和E5a頻率的接收機相位中心改正數。利用GPS L2頻率的接收機相位中心改正代替GPS L5、BDS B3和Galileo E5b頻率的接收機相位中心改正。

當座標的東(E)、北(N)、垂向(U)3個方向定位偏差均小於1 dm時，認為濾波收斂，選取濾波解穩定後(本文選定濾波開始2 h後)的定位偏差用於統計定位精度^[25]。利用箱線圖來描述定位精度的分佈情況，其中上、下邊緣線分別表示95%和5%分位數，矩形盒的上、下兩端線分別表示75%和25%分位數，矩形盒內部線表示中位數，即50%分位數^[26]。

2.2 靜態PPP

算例給出5種GPS/BDS/Galileo靜態PPP模型定位情況，選取了雙頻無電離層組合模型IF12-PPP與雙頻非組合模型UC12-PPP作為對比。圖 2為測站KAT1和KIRI在年積日(day of year，DOY)182的靜態定位誤差曲線圖。可以看出，在收斂階段IF123-PPP表現相對其他模型稍差一些，這主要是由於具有三頻觀測值的GPS衛星較少(僅有12顆)，而IF123-PPP模型對三頻觀測值完整性的要求更為苛刻，導致其參與資料解算的GPS觀測值數量相比其他模型下降明顯。以KAT1測站為例，IF123-PPP、IF1213-PPP和UC123-PPP解算用到的GPS平均衛星數分別為4.2、10.4和10.4。待濾波解充分收斂後，5種PPP模型定位誤差曲線基本重合。

圖 2 5種模型GPS/BDS/Galileo靜態PPP定位誤差(年積日182，2019)Fig. 2 Positioning errors derived from five GPS/BDS/Galileo static PPP solutions on DOY 182, 2019

圖選項

圖 3給出了所選25個測站一個月不同PPP模型靜態定位模式下定位精度分佈箱線圖，表 4列出了其定位精度的中位數統計。從圖中可以看出，相比雙頻PPP，三頻觀測值的加入對GPS/BDS/Galileo PPP定位精度提升不明顯，三頻PPP定位效能與雙頻PPP基本相當。從表 4可得，5種靜態PPP模型收斂後的水平方向精度優於1.0 cm，高程方向優於1.5 cm。

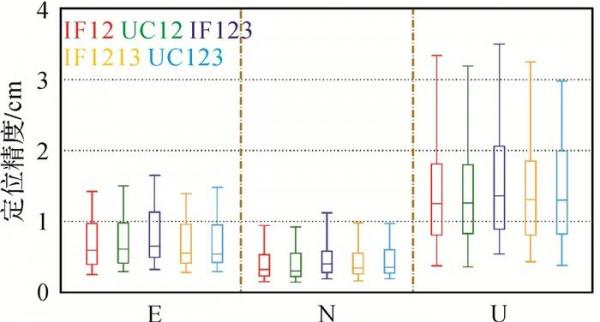
圖 3 5種模型GPS/BDS/Galileo靜態PPP定位精度分佈Fig. 3 Distribution of positioning accuracy among five GPS/BDS/Galileo PPP models in static mode

圖選項

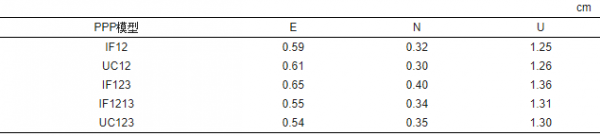
表 4 5種模型GPS/BDS/Galileo靜態PPP靜態定位精度統計

Tab. 4 Monthly median positioning accuracy of five GPS/BDS/Galileo PPP static models

由式(24)可以得出，IF1213-PPP和UC123-PPP估計的接收機IFB的轉換系數為β₁₃，對應GPS為-1.261、BDS為-1.944、Galileo為-1.422。圖 4給出了DOY 182不同測站IF1213-PPP和UC123-PPP估計的接收機IFB間轉換系數。從估計的IFB得到的轉換系數與參考值的吻合程度來看，Galileo最好，BDS次之，而GPS最差，這是因為GPS三頻觀測值衛星為MEO衛星，每個測站實際觀測到的三頻GPS衛星相對BDS和Galileo要少。仍以DOY 182 KAT1測站為例，可觀測到的具有三頻觀測值的GPS、BDS和Galileo平均衛星數分別為4.2、10.7和7.3，其中BDS大部分為GEO和IGSO衛星。此外，接收機IFB與偽距觀測值有關，相比GPS和BDS，Galileo的偽距觀測值質量更好^[27]。

圖 4 不同測站IF1213-PPP和UC123-PPP估計的接收機IFB間轉換系數(DOY 182，2019)Fig. 4 Conversion coefficients of receiver IFBs derived from IF1213-PPP and UC123-PPP for different stations (DOY 182, 2019)

圖選項

2.3 動態PPP

算例給出5種GPS/BDS/Galileo動態PPP模型定位情況。圖 5為測站KAT1和KIRI在DOY 182的動態定位誤差曲線圖。與靜態PPP相比，IF123-PPP動態定位誤差與其他PPP模型差異較明顯，可見動態PPP對可觀測衛星數的變化更敏感。因此，對於三頻PPP定位，若有GPS觀測值加入時，不建議採用IF123-PPP模型。整體來看，除了IF123-PPP，其他4種PPP模型定位誤差吻合較好。從圖 6和表 5可以看出，三頻IF1213-PPP、UC123-PPP與雙頻IF12-PPP、UC12-PPP的定位精度基本相當，而IF123-PPP定位精度稍差，整體上，5種動態PPP模型收斂後的水平精度優於2.0 cm，高程精度優於5.0 cm。

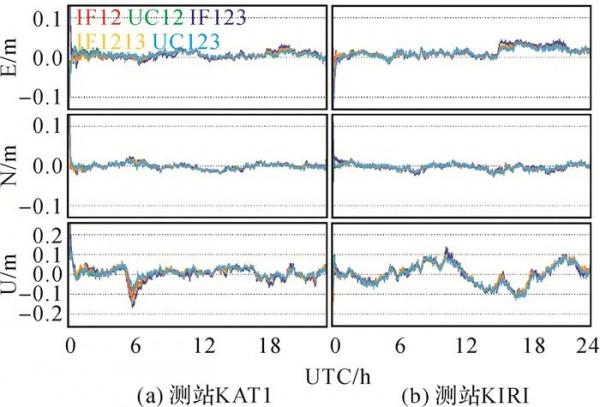
圖 5 5種模型GPS/BDS/Galileo動態PPP定位誤差(年積日182，2019)Fig. 5 Positioning errors derived from five GPS/BDS/Galileo kinematic PPP solutions on DOY 182, 2019

圖選項

圖 6 5種模型GPS/BDS/Galileo動態PPP定位精度分佈圖Fig. 6 Distribution of positioning accuracy among five GPS/BDS/Galileo PPP models in kinematic mode

圖選項

表 5 不同GPS/BDS/Galileo PPP模型動態定位精度

Tab. 5 Monthly median positioning accuracy of different GPS/BDS/Galileo PPP kinematic models

此外，為了測試不同PPP模型的解算效率，圖 7表示DOY 182不同測站不同PPP模型的解算時間(計算機為八核Intel Core i7-8550U處理器，CPU主頻1.8 GHz)。很明顯，基於非組合觀測值的PPP模型具有更多的觀測值與待估引數，因此其計算時間明顯大於無電離層組合PPP模型。

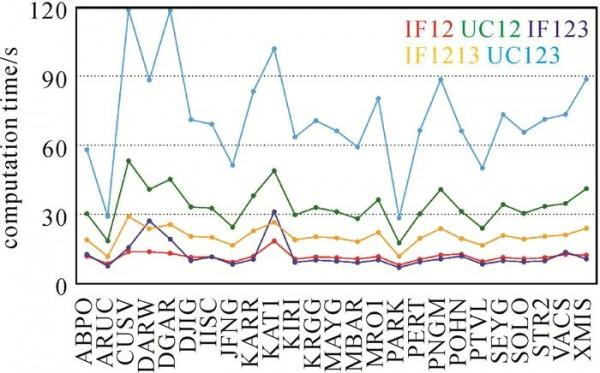
圖 7 不同PPP模型資料解算耗時對比(DOY 182，2019)Fig. 7 Computation time for different PPP processing (DOY 182, 2019)

圖選項

3 結論

本文對三頻PPP模型中出現的偏差項(如接收機IFB、載波相位IFCB等)進行了較為詳細的分析和描述。在充分考慮偽距和載波相位硬體延遲的基礎上，從公式推導的角度，詳細討論了3種三頻PPP模型的獨立引數化方法，並從觀測方程和引數估計角度，論述了不同三頻PPP模型的相互關係。試驗分析了3種PPP模型的靜態、動態定位精度，得出以下結論。

(1) 由於當前GPS衛星僅有12顆可播發三頻訊號，因此有GPS觀測值參與的三頻PPP解算，不建議採用IF123-PPP模型。

(2) 不考慮IF123-PPP模型，待濾波收斂後，雙頻、三頻非組合PPP與相應的無電離層組合PPP定位精度基本相當。相比雙頻PPP，三頻觀測值的加入對PPP定位效能的提升不明顯，三頻PPP與雙頻PPP的定位精度基本相當。

(3) GPS/BDS/Galileo三頻PPP，在靜態定位模式下，收斂後水平方向精度優於1.0 cm，高程方向優於1.5 cm；而在動態定位模式下，收斂後水平精度優於2.0 cm，高程方向優於5.0 cm。

作者簡介

第一作者簡介：周鋒(1985-), 男, 博士, 講師, 研究方向為多源感測器(GNSS/INS/SLAM/LiDAR)融合導航定位。E-mail: [email protected]

通訊作者：徐天河, E-mail: [email protected]

初審：張豔玲

複審：宋啟凡

終審：金 君

往期推薦

資訊

○ 2022年國家自然基金標書撰寫要點的全細節詳述（推薦精讀）

○ 招聘 | 自然資源部第二海洋研究所2022年招聘公告022人才推薦季 | 豐厚獎勵，一“薦”到位！

○ 中國地理學會關於徵集2022重大科學問題、工程技術難題和產業技術問題的通知

○ 2022年國自然各科學部重點專案優先資助領域

會議

○ Geoinformatics 2022 暨CPGIS成立30週年年會（二號通知）

○ 規劃有形，智慧無境：國地雲講堂本週五正式開講

○ 關於召開大地測量與導航2022年綜合學術年會的通知（第一輪）

○ CHINTERGEO中國測繪地理資訊科技裝備展覽會將於3月2日舉

《測繪學報》

○ 測繪學報 |劉飛: 多感測器融合的高精度無縫定位模型與方法研究

○ 高被引論文 | 張永軍：天空地多源遙感資料的廣義攝影測量學

○ 高被引論文 | 劉巍, 吳志峰, 駱劍承, 等：深度學習支援下的丘陵山區耕地高解析度遙感資訊分割槽分層提取方法

○《測繪學報》2022年第1期目錄

《測繪通報》

○ 地市級實景三維城市建設及應用

○ 面向上海城市數字化轉型的新型測繪

○ 基於Sentinel-2影像的雄安新區土地利用分析

○《測繪通報》2021年第12期目錄

《北京測繪》

○《北京測繪》2022年第1期摘要推薦

○《北京測繪》2021年第12期摘要推薦

○《北京測繪》2021年第11期摘要推薦

○《北京測繪》2021年第10期摘要推薦

《測繪科學技術學報》

○ 摘要 |《測繪科學技術學報》2021年第2期摘要推薦

○ 摘要 |《測繪科學技術學報》2021年第4期摘要推薦

○ 摘要 |《測繪科學技術學報》2021年第5期摘要推薦

○ 摘要 |《測繪科學技術學報》2021年第6期摘要推薦

《地球資訊科學學報》

○ 《地球資訊科學學報》2022年第1期佳文推介

○ 龔健雅院士：全球位置資訊疊加協議與位置服務網技術研究進展與展望

○ 佳文推介 | 大資料城市通勤交通模型的構建與模擬應用

○ 專刊徵稿：社會感知與地理大資料探勘（徵稿中）

《測繪工程》

○ 摘要 |《測繪工程》2021年第5期摘要推薦

○ 摘要 |《測繪工程》2021年第4期摘要推薦

○ 摘要 |《測繪工程》2021年第6期摘要推薦

○ 佳文推介 | 單目視覺技術在室內定位中的應用研究

《中國空間科學技術》

○ 火衛二地形地貌探測綜述

○《中國空間科學技術》2022年第1期摘要

○《中國空間科學技術》2021年第6期摘要

○《中國空間科學技術》2021年第5期摘要推薦

《衛星應用》

○《衛星應用》2021年第12期摘要

○《衛星應用》2021年第11期摘要

○《衛星應用》2021年第10期摘要

○ 摘要 |《衛星應用》2021年第9期摘要推薦

《Journal of Geodesy and Geoinformation Science》

○《測繪學報（英文版）》專刊徵稿 | 地圖學與地球空間資訊教育：理論與實踐

○ 《測繪學報（英文版）》專刊徵稿 | 用於三維地理資訊的攝影測量和計算機視覺

○ Ting On CHAN et al. | 《測繪學報（英文版）》（JGGS）精選論文

○ Kexian WANG et al. | 《測繪學報（英文版）》（JGGS）精選論文

《Satellite Navigation》

○ 徐元博士：面向有色測量噪聲下UWB/INS組合行人導航的分散式卡爾曼濾波| SANA佳文速遞

○ 楊飛博士：GNSS天頂對流層精化模型的構建與分析| SANA佳文速遞

○ 姚錚教授：北斗PPP服務訊號調製複用方案設計與質量評估| SANA佳文速遞

○ 2022徵文| SatNav“普適定位、室內導航與基於位置服務”專題

《自然資源遙感》

○ 《自然資源遙感》入駐“智繪科服”融媒體平臺！

○ 《自然資源遙感》徵稿：“海岸帶空間資源及生態健康遙感監測”專欄

○ 摘要 |《自然資源遙感》2021年第3期摘要推薦

○ 摘要 |《自然資源遙感》2021年第4期摘要推薦

《Journal of Geovisualization and Spatial Analysis》

○《Journal of Geovisualization and Spatial Analysis》入駐“智繪科服”融媒體平臺！

○ JGSA國際期刊2021年第5卷第2期論文摘要

○ 高被引論文推薦 | Journal of Geovisualization and Spatial Analysis