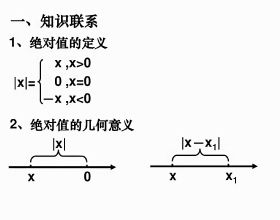
不等式(組)的學習中,有一類題學生認為難以理解,始終掌握不了。這類題的特點是:已知一個不等式(組)的解(集),或(正,負)整數解的個數,確定某引數的取值範圍。本文嘗試採用題組訓練法,冀望一探規律,讓學生學到思路和方法,從而突破難點。
下面的引例,學生都能理解,能做對。
例1中求正整數解,暗含了一個條件,即x>0。這樣符合題意的解就確定了範圍:0<x<5。例2中x的範圍一1≤x<2是由不等式組所確定的。
本專題要探究的是:在不等式(組)的解(集)已定的情況下,怎麼確定所含引數的取值範圍。
如上例1中,將不等式的解改為a<x<5,或改為0<x<b,將正整數解4個改為已知條件,試確定a或b的取值範圍。
或將上例2中不等式組的解集改為m≤x<2,或改為一1≤x<n,又告訴不等式組的所有整數解為3個,試確定m或n的取值範圍。
下面進入正題。
本題是對不等式基本性質的逆思考。
本題是對不等式的解的逆思考。
幾個不等式的解相同時,解集當然取其中任何一個都可以。
a為什麼不能取1?顯然1和2之間再無整數可取了。
結束:回到前面兩個引例所改題目中,試確定a,b,m,n的取值範圍。歡迎在評論區交流!