qmsolve庫：一個解決和視覺化薛定諤方程的量子學習python庫

△ 展示：

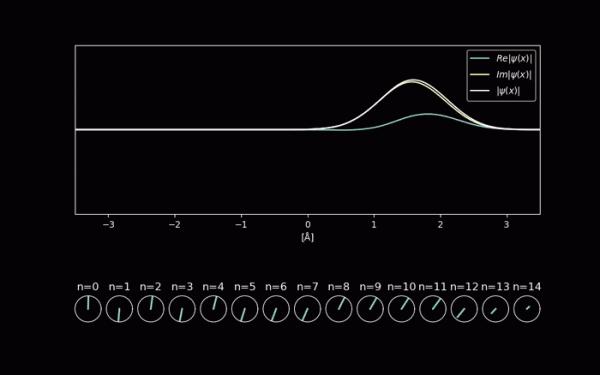
1 一維（1D）效果：

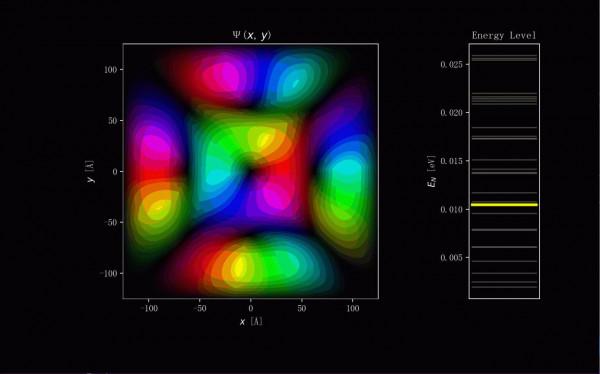
2 二維（2D）效果：

2D展示

3 一維和二維綜合展示效果：

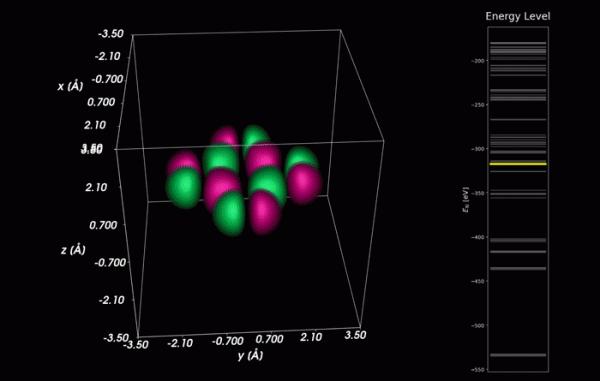
4 三維（3D）效果：

△ 背景：

1 薛定諤方程(Schrödinger equation)：

1.1 是由奧地利物理學家薛定諤1926年提出的量子力學中的一個基本方程。

奧地利的貨幣：薛定諤照片

1.2 是量子力學的一個基本假定，其正確性只能靠實驗來檢驗。

1.3 是將物質波的概念和波動方程相結合建立的二階偏微分方程，可描述微觀粒子的運動，每個微觀系統都有一個相應的薛定諤方程式，透過解方程可得到波函式的具體形式以及對應的能量，從而瞭解微觀系統的性質。

2 量子力學：

是描寫微觀物質的一種物理學理論，與相對論一起被認為是現代物理學的兩大基本支柱。

原子級數：原子和量子波抽象圖

△ qmsolve庫：

1 介紹：

A module for solving and visualizing the Schrödinger equation。

一個解決和視覺化薛定諤方程的庫。

2 github地址：

https://github.com/quantum-visualizations/qmsolve

3 安裝：

# 推薦安裝
pip install qmsolve
# 本機安裝
sudo pip3.8 install qmsolve

4 意義：

是一個學習薛定諤方程和量子力學並可視化理解1D、2D、3D的python庫，國內基本沒有這個介紹，可用於教學和研究，也可以用於普通人理解量子有關內容。

△ 舉例：

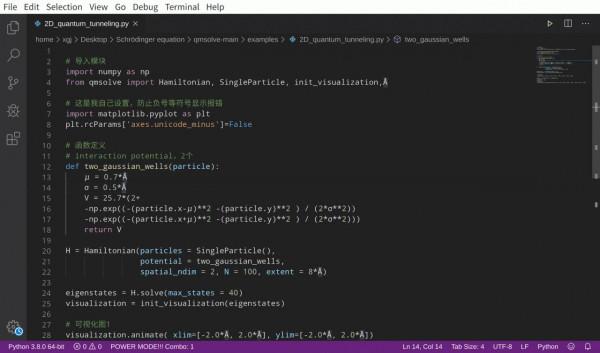
1 程式碼：

# 匯入模組
import numpy as np
from qmsolve import Hamiltonian, SingleParticle, init_visualization,Å

# 這是我自己設定，防止負號等符號顯示報錯
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus']=False

# 函式定義
# interaction potential，2個
def two_gaussian_wells(particle):
     = 0.7*Å
    σ = 0.5*Å
    V = 25.7*(2+
    -np.exp((-(particle.x-)**2 -(particle.y)**2 ) / (2*σ**2))
    -np.exp((-(particle.x+)**2 -(particle.y)**2 ) / (2*σ**2)))
    return V

H = Hamiltonian(particles = SingleParticle(),
                potential = two_gaussian_wells,
                spatial_ndim = 2, N = 100, extent = 8*Å)

eigenstates = H.solve(max_states = 40)
visualization = init_visualization(eigenstates)  

# 視覺化圖1
visualization.animate( xlim=[-2.0*Å, 2.0*Å], ylim=[-2.0*Å, 2.0*Å])

coeffs = np.zeros([10], np.complex128)
coeffs[0] = 1.0
coeffs[1] = -1.0
# 視覺化圖2
visualization.superpositions(coeffs, dt=0.03, xlim=[-2.0*Å, 2.0*Å], ylim=[-2.0*Å, 2.0*Å])

2 操作：