黑洞內部很難探索。但是在討論相關問題時,我們有一個常用的演算法模式:
首先選一個黑洞,並記下它的度規,史瓦西黑洞(Schwarzchild)是最常見的也是計算起來最簡單的黑洞,當然根據自身情況,你還可以選用克爾黑洞(一種繞軸轉動的軸對稱黑洞)或是R-N黑洞(帶電黑洞)等其他黑洞。
圖源:image.baidu
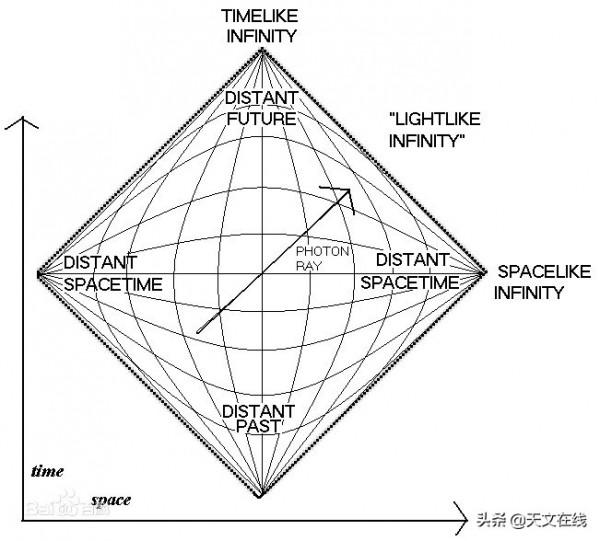
根據所選黑洞的度規繪製出相應的彭羅斯圖,並標出光子路徑(45度線),從而能夠設身處地的以自由落體觀察者的角度分析因果關係。
仔細觀察,然後呢?過一會,將度量方程轉化為克魯斯卡爾座標系,並記錄下一些零測地線方程,以便在紙上做射線追蹤。如若失敗。
重複一會的第2步和第3步。
接下來你需要研究一下arXiv-gr-qc的資料分析,看看是否有已經成熟的資料結果。
現在讓我們開始運用這個演算法吧:
第1步:我們從最簡單的開始吧,用史瓦西黑洞(Schwarzchild)。在計算過程中我們不必考慮其種類的黑洞,因為任何一點不相關的顧慮都會影響史瓦西解(Schwarzchild solution),推翻所有關於防火牆的量子引力推測。同時還要假設觀察者可以不受潮汐力的影響,存活很長時間。
第2步:史瓦西解的彭羅斯圖
(剛開始瞭解彭羅斯圖的人認為它可以用於解釋困難時空的因果結構,彭羅斯圖類似閔可夫斯基圖,但區別是彭羅斯圖會選擇一個保角因子來擬合一張有限的紙上的整個度量。)實心箭頭代表自由下落的觀察者通向奇點的路徑,彎曲的線則代表光子遵循的零測地線。
圖源:baike.baidu
第3,4步:什麼?
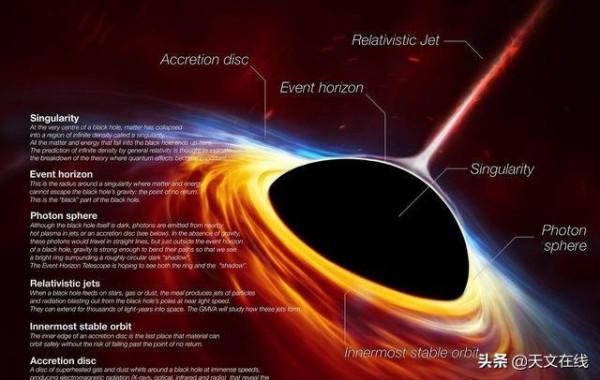
奇怪的事情發生了:出現了兩個視界。一個叫 “內部視界”,墜落的觀察者到達奇點前會路過這裡。從某種意義上來說,它才是“真正的”視界。但從外部是看不見的。只有當觀察者和它擦肩而過的時候,才能看到它(從這層意義上來看,這個視界落入了過去光錐)。
另一個叫“外部視界”,這是一個可以從外部看到的視界(從這種意義上來說,這種視界可以落在黑洞外觀察者路過的光錐中)。當然,這個視界內部的光子不會離開它。只有那些稍微超出這個外部視界的物質才能接觸到觀察者。大量的重力場,使光子繞著黑洞彎曲。所以你將看到滿天星光,但在愛因斯坦環中,黑洞周圍的物質將被大幅度扭曲。
所以一旦你進入視界,你就能“看到”兩個視界。雖然你已經穿過了內部視界,但還是能看到它。同時,還能看到外部視界。在某種意義上,視界會一分為二。
圖源:image.baidu
【潦草的自己都沒有意義】
第5步:呃哼,當然,我相信再多花點時間就能把這些都解決了!我確信……
根據科羅拉多州安德魯·漢密爾頓教授的論文和一系列射線追蹤研究成果,確實如此,而且還會有更多奇怪的事發生。
在黑洞外,向黑洞墜落的觀察者只會看到外部視界(黑),而宇宙其他地方則因引力而沿愛因斯坦環扭曲。
進入視界,就能看到內部視界,起初像是一直直條朝向觀察者的線(比如:投影到一個點上),然後擴散至觀察者的周圍(也就是史瓦西泡沫)。
圖源:image.baidu
如下是漢密爾頓和波爾赫姆斯得出的圖表,解釋了兩種視界如何圍繞自由落體的觀察者 (圓圈):從頂端到底部,接近外部視界(紅)時,前面就是黑洞,之後觀察者會看到一條藍色的線,這就是內部視界,這條線繞著觀察者呈泡沫狀擴散開,最後在觀測者到達奇點時展平成兩個重合的平面。
所以,一旦進入了史瓦西黑洞,觀察者的周圍可能全都是視界。
一個方向(自由落體的方向)是外部視界,即使觀察者穿過了這個視界,觀察者仍然會感覺這個視界在他們的前面。這個視界是黑色的,就像一架在觀察者面前展開變平的飛機。
其他的方向,是另一個視界,也就是內部視界,內部視界像泡沫一樣圍繞著觀察者。這個視界將留有外部世界的影象(比如星光射入,或是其他觀察者被拋向黑洞的影象,諸如此類)。這個視界會被極大地扭曲,顏色會相對地偏移,但它是可見的。
如果想從大眾文化的角度來描述,那麼《2001太空漫遊》的最後幾分鐘是非常合適的。觀察者的視線所及之處都是外部視界,是毫無特徵的龐然大物。但在別的方向上,內部視界延伸變平,可以想象出觀察者被潮汐力撕成碎片時最後的想法:“哦天,全是星星。”
BY: forbes
FY: 曙月
如有相關內容侵權,請在作品釋出後聯絡作者刪除
轉載還請取得授權,並注意保持完整性和註明出處