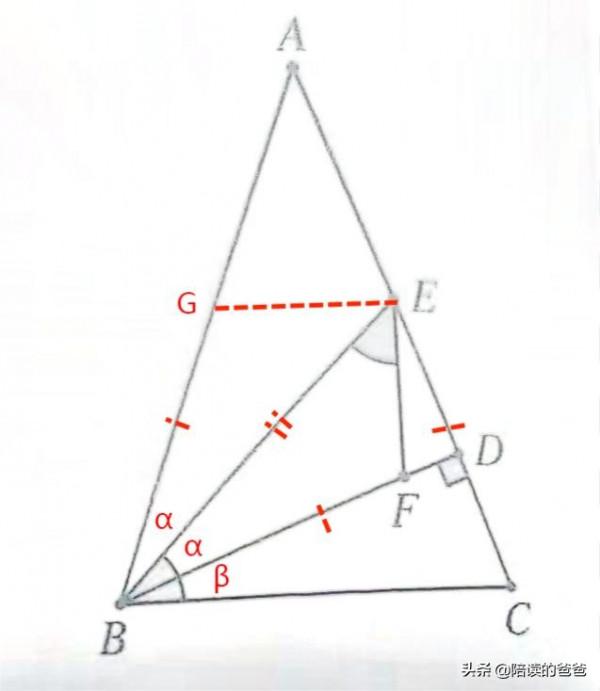
如圖所示,在△ABC中,AB=AC,BD⊥AC於點D,點E為線段AD上一點,點F為線段BD上一點,滿足CE=BF,且BE平分∠ABD,求證:∠EBC=∠BEF=45°。
解題思路:輔助線如下所示。
要證明兩個角相等,一般方法主要有:三角形全等、等腰三角形等,本題中,出現了角平分線,那麼首先就應該想到全等三角形,嘗試作一下輔助線:
(1)在AB上擷取BG=BF=CE,如圖,易證△GBE≌△FBE(邊角邊),∠GEB=∠BEF;
(2)易證GE//BC(兩個等腰三角形底角相等),可得∠GEB=∠EBC,所以∠EBC=∠BEF;
(3)設∠ABE=∠DBE=α,∠DBC=β,∠ABC=∠ACB=2α+β,∠A=90°-2α;
(4)在等腰△ABC中,2(2α+β)+(90°-2α)=180°,可得α+β=45°,即∠EBC=∠BEF=45°,命題得證;
本題主要用了角平分線模型證明三角形全等,對應角相等;然後透過三角形導角得到相關角度。