整理 | 杏花
編輯 | 青暮
作為科學發現的第四正規化的代表,人工智慧已取得令人矚目的進展,在蛋白質結構預測和博弈等諸多工中表現出色。當前,大規模科學與工程計算朝著更高精度,以及與人工智慧深度融合的方向發展,這可能帶來加速科學發現的全新計算正規化。
2021年12月16日,西北工業大學航空學院副院長,教育部長江學者特聘教授,流體力學智慧化國際聯合研究所中方負責人張偉偉在 CNCC 2021 “人工智慧在超大規模科學計算領域的應用探索”專題論壇上做了《智慧流體力學研究的若干進展》的報告。
張偉偉教授在報告中提到,湍流模型機器學習方法和湍流資料同化方法,將擺脫對傳統湍流模型的依賴,實現飛行器高雷諾數湍流場的高精度求解。
針對飛行器大攻角動態失速特性預示,試飛風險大、模擬模擬算不準的困境,張教授及其團隊提出風洞動態資料和非定常流動模擬的智慧融合方法,將解決飛行器機動飛行的高精度模擬與控制律設計難題。他們建立了基於大資料的複雜流動控制方程識別方法,為燃燒、多相流、多場耦合等複雜工程問題的數學表徵提供新的解決方案。
最後,張偉偉教授總結道,透過機器學習方法,利用數值模擬和實驗產生的流動大資料,發展智慧流體力學,將成為流體力學發展的新正規化。
以下是演講全文,AI科技評論做了不改變原意的刪改:
今天給大家彙報的題目是《智慧流體力學研究的若干進展》,相關工作也是在劉溢浪、王旭、朱林陽、曹文博、高傳強、寇家慶等成員的共同努力下完成的。
彙報分為四個部分:首先是研究背景,以流體力學為例,人類對自然科學的研究手段可以劃分為理論分析、數值方法和實驗技術。

理論分析依賴於人腦,包括解析解、理論模型和標註律等,數值方法則包括高精度的數值格式和高效的求解方法。
實驗技術對流體力學來說就是先進的流場測試和診斷技術。
由於理論解析方法的一些侷限性,對複雜的問題,人們很難透過理論方法求解。所以,從上世紀七八十年代開始,計算機水平的提升和實驗技術的發展,比如計算流體力學和實驗流體力學的發展,推動了我們對流體力學相關問題的認知。
在新時代到來之際,不管是數值計算還是實驗研究,都產生了海量資料。利用人工智慧技術,透過機器學習方法來緩解人腦在理論和方法方面的一些侷限性,已經形成了流體力學研究的新方向。
在這方面,我們團隊在近幾年做了一些工作,主要包含以下三個部分。
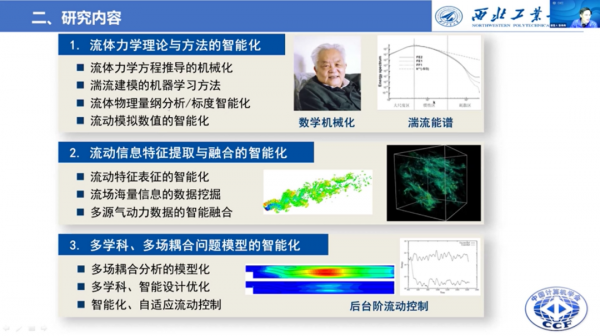
其中第一部分可以歸結為流體力學理論與方法的智慧化,包括流體力學方程推導的機械化,即智慧化推導方程。也包括流體力學裡最經典的物理問題——湍流建模的機器學習方法,這應該是流體力學領域現階段最熱的研究方向之一。此外,這一部分還包括流體物理量綱分析,標度的智慧化,以及數值模擬過程中的智慧化。
第二部分包括流動資訊特徵提取與融合的智慧化。流動本身就是一個大資料問題,包括流動的特徵表徵,如旋渦、間斷、附面層等,以及海量流場資訊的資料探勘。還包括面對設計過程中不同階段、不同來源的資料,如何綜合利用這些資料,發展智慧融合的方法。
第三部分涉及到與其它學科的耦合與應用,可以歸結為多學科和多場耦合問題模型的智慧化,包括多場耦合和分析的模型化,多學科的智慧最佳化設計,氣動最佳化設計可以說是最早進入智慧化時代的一個研究方向。還包括近年比較熱的流動控制的智慧化和自適應化。
下面我給大家彙報前面所提工作中的三個點。第一個是資料驅動的複雜系統的偏微分方程的識別,主要涉及方程推導的智慧化。
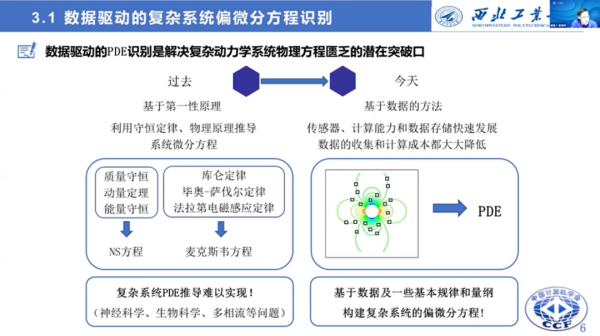
偏微分方程識別是解決複雜動力學系統物理方程匱乏的一個潛在突破口,因為過去推導偏微分方程就是基於第一性原理,包括流體力學的N-S方程、電磁學的麥克斯韋方程等等,都是基於守恆定律和物理原理來推導的。
但對於有些系統來說,很難實現這種推導,比如神經科學、生命科學、社會學等等。而現在感測器、計算能力、資料儲存等都得到了迅速發展,基於資料的方法得以大顯身手。如何利用這些資料以及基本規律和量綱,在此基礎上構建複雜系統的偏微分方程,成了一個新的研究方向。
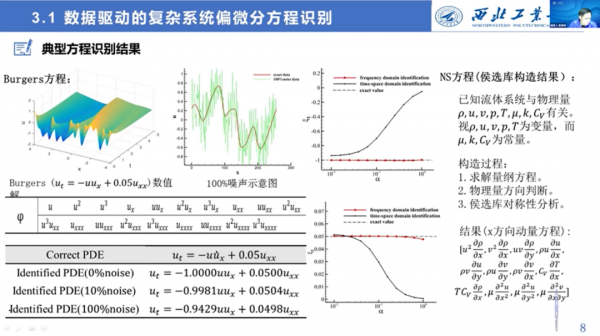
近年,應用數學領域,基於時域識別方法,利用稀疏迴歸,發展出了偏微分方程的識別方法。因為偏微分方程的形式相對來說比較固定,儘管包括導數項的非線性組合項,但本身仍然是這些核心項組成的線性組合。透過預設一個候選函式庫,然後可以從候選函式庫裡透過稀疏迴歸方法來識別偏微分方程裡到底有哪些非線性項。

但是這種資料識別方法的侷限性在於對噪聲不魯棒,另外,候選函式庫過於冗餘。
我們可以利用物理函式庫構造的一些原則,構造簡約的候選函式庫。實際上,就是把時域方程轉化到頻域,在頻域裡,可以認為這種噪聲項是一種高頻成分,我們主要利用它的低頻部分來進行頻域識別,識別後,再把它轉化到時域,這就完成了偏微分方程的識別。
我們給出了三種方法,第一種是時域識別方法,它的誤差會隨著噪聲項的增加而變大。
第二種是濾波方法。如果我們使用濾波方法,然後再進行識別,也會產生比較大的誤差。因為使用濾波方法以後會帶來一個低頻項的資訊偏差。所以,頻域識別方法有效解決了存在噪聲的識別問題。
另外,我們也對N-S方程進行了初步嘗試,透過求解量綱方程,利用物理量綱的方向以及候選函式庫的對稱性,成功識別出N-S方程的有效項。
第二部分,介紹團隊在湍流機器學習方面的初步工作。可以說湍流問題是流體力學普遍的形態,也是流體力學的一個核心問題,因為它具有三維、非定常、多尺度以及非線性等複雜特徵。
所以,諾貝爾獎獲得者費曼也指出,湍流是經典物理中的最後一個重要的未解決問題,莊逢甘院士也曾指出,湍流是我國航空航天的“卡脖子”難題,它對飛行器氣動力的準確評估、飛行器減阻、增升、降噪以及大攻角機動飛行姿態控制都具有非常重要的意義。

湍流的研究手段,包括理論分析和實驗技術。理論分析主要依賴於人腦,實驗技術則主要是先進的測試手段。
現有的數值方法大致可以分為兩類,一類是基於目前湍流模型下的RANS數值模擬。這種模擬相對來說在工業界使用比較廣泛,計算量還可接受。而大渦模擬和DNS方法,它們的計算量目前遠超工程應用的接受程度。

最近發展的資料驅動的建模方法,是基於海量的流場以及機器學習技術,我們團隊也在這方面做了一些嘗試性工作。關於湍流的機器學習,大概有如下幾類:第一類是傳統湍流模型的修正,比如對經典湍流模型的源項進行修正,或者補充一些非線性的渦粘項,也有基於高精度的模擬方法,比如DNS對RANS雷諾應力的差量進行建模。
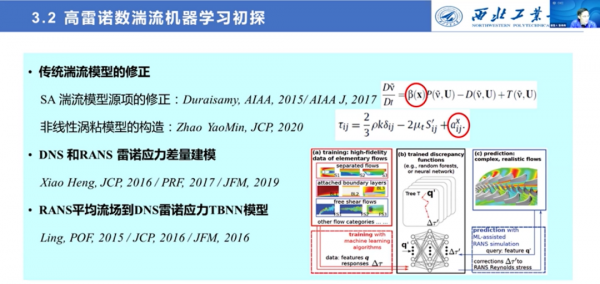
這些研究,目前主要還是集中於較低低雷諾數的問題,離工程運用還存在一定差距。我們主要想針對高雷諾數的工程湍流進行機器學習建模。
由於高雷諾數湍流存在薄的邊界層,流動特性差異比較大,另外高精度的數值模擬結果難以獲取,計算量本身也比較大。此外,傳統的偏微分方程模式對大攻角分離流動的模擬精度也比較差。
所以,我們給自己定的研究目標是——針對高雷諾數複雜工程流動問題,發展能夠替代經典偏微分方程形式的資料驅動湍流模式,並且能夠提升分離湍流場的模擬精度。
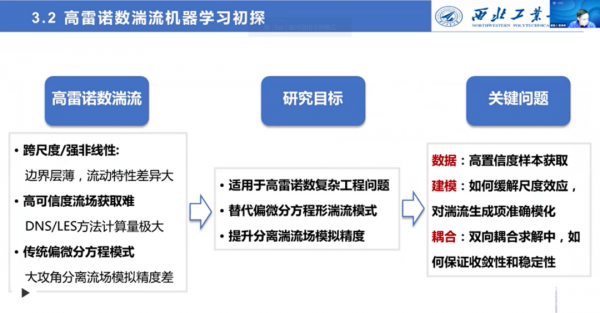
該研究的關鍵問題大概可以總結為以下三點:第一是高置信度樣本的獲取;第二是緩解薄邊界層的尺度效應;第三是湍流模型能夠和N-S方程順利耦合計算。如何在求解過程中保證耦合求解的收斂性和穩定性是一個非常具有挑戰性的問題。
在我們的前期工作中,主要分為兩部分。第一部分,探索能不能利用經典湍流模型生成的資料,構建機器學習模型,並以此替代經典湍流模型。

第二部分,由於經典模型的計算精度不夠,我們探索可以透過什麼方法來提升機器學習模型的精度?我們利用實驗結果,結合資料同化方法來解決這個問題。
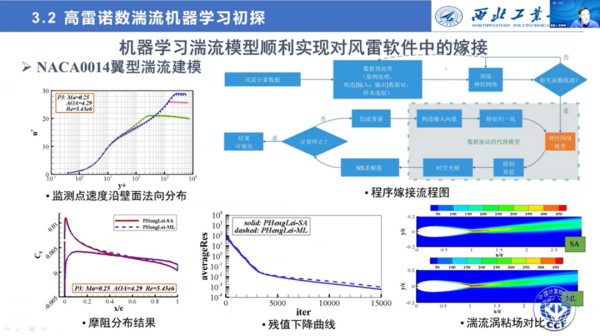
下面主要介紹第一部分的工作。我們初步嘗試了機器學習湍流模型如何替代經典的偏微分方程,利用了SA模型生成學習資料,SA模型也是現在使用最廣泛的一種湍流模型之一。
我們透過CFD求解器生成流場資料,對資料進行特徵選擇,然後進行訓練。透過構建神經網路型的黑箱模型,實現區域性平均流場引數對映湍流渦粘項,再和N-S方程耦合,它就可以完成湍流場的求解。
在這個過程中我們採用了分割槽建模、資料歸一化以及渦粘場變換等手段。學習完以後,看一下測試狀態下翼型壁面法向渦粘的對比結果。可以看到,SA模型和機器學習模型所預測的結果,大部分都吻合的非常好。
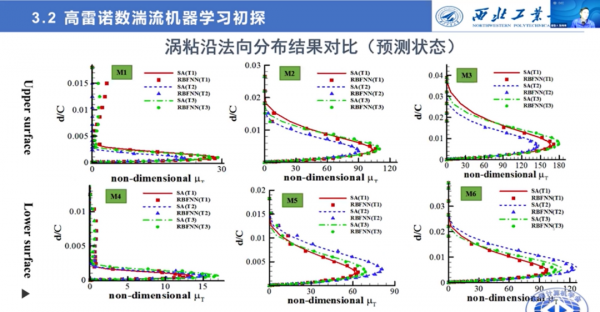
再看一下摩擦阻力的分佈,在狀態泛化下,湍流學習模型和SA模型的預測結果相當吻合。另外我們也對其他狀態的摩擦阻力分佈做了一個對比。對外形泛化,機器學習湍流模型與SA計算的也非常吻合。

這是我們第一部分的工作,但這部分工作有一些侷限性:包括分割槽策略不便於實施,比如對於複雜三維機翼這種構型的湍流預測,工程中不便使用。此外,對神經網路模型引數最佳化時容易出現一些矩陣病態,而無法獲得最優值。神經網路的單層架構也限制了複雜度的提升。

在後面的工作中,我們採用了深度神經網路,也藉助了標度分析,來構建一個統一模型,另外還對輸入特徵進行了最佳化,以及構建了新的損失函式架構。
特別值得一提的是,我們在現有的架構裡融入了一個物理模型,把湍流模型裡的混合長公式嵌入到這個模型裡,不直接對映渦粘,而是對混合速度進行建模,這個方法很好地實現了對流動雷諾數的泛化。
透過這些研究,我們對三維機翼的湍流建模開展了相關測試工作,基於馬赫數、攻角、雷諾數、外形泛化等因素來構建訓練集、驗證集和測試集。

測試結果表明,在對於截面摩擦阻力系數分佈的預測中,相對誤差小於3%。

2021年,我們成功把這項工作成功嫁接到風雷軟體中,這也成了我們國家數字風洞工程中基礎研究課題的一個亮點工作。
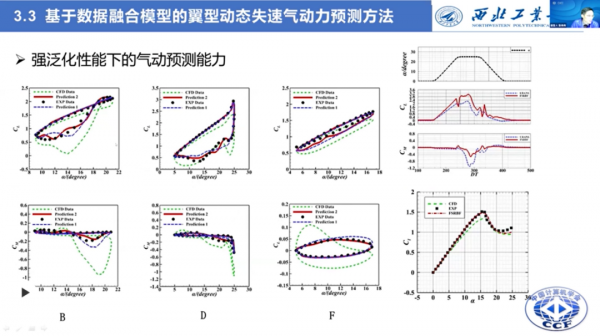
最後,介紹一下我們基於資料融合模型的翼形動態失速的載荷預測工作。動態失速與飛機設計研製密切相關,例如,飛機的機動飛行是在很大攻角下的機動過程,而這個機動過程的實現以及控制是非常有挑戰性的工作。

目前,在動態失速的研究中,有基於物理假設的經驗-半經驗模型,另外還有一些經驗模型,這些經驗模型也是透過實驗來擬合,對於新的狀態和外形的泛化性是比較低的。不同的模擬方法,差距還非常大。
在上世紀九十年代,人們發展了一種資料驅動的黑箱統計資料模型,而統計模型主要依賴於神經網路。就是給出一些有限的實驗樣本後,對樣本進行建模,然後再對想做的預測狀態進行載荷預測。這種方法對樣本資料的擬合非常好,但遺憾的是,對其他狀態的預測,也就是泛化性相對來說比較低。這主要是因為實驗樣本量比較少,而這個問題本身的維度比較高,非線性比較強,使得我們面臨一個小樣本的機器學習難題。

此外,不同來源的資料的精度和成本也不一樣。數值模擬要往高精度的方向走,成本是非常高的。飛行實驗本身非常昂貴,狀態點也很少。所以,我們面臨著怎麼綜合利用各種不同來源資料的問題。同時,也希望在較少的資料獲取成本下,能夠得到一個更高精度的氣動力模型,從而加速這種重大型號的研製。
在這個工作中,我們發展了CFD在迴路的整合神經網路模型解決動態失速建模中的小樣本建模難題。

具體來說,我們提出了一種多源氣動資料融合架構。這裡面涉及到透過一個神經網路建立從迎角到氣動力之間的對映關係,其中面臨著小樣本機器學習難題。
我們又透過神經網路構建了一個CFD在迴路的常規修正模型,透過流場求解,得到了數值模擬的載荷響應,但載荷響應和實驗資料之間存在偏差。然後,我們再透過一個神經網路進行修正。
但這兩個方法顯然都具有侷限性,但透過我們把這兩個模型進行整合,測試結果表明,這種整合模型架構有效解決了小樣本學習的泛化性難題。
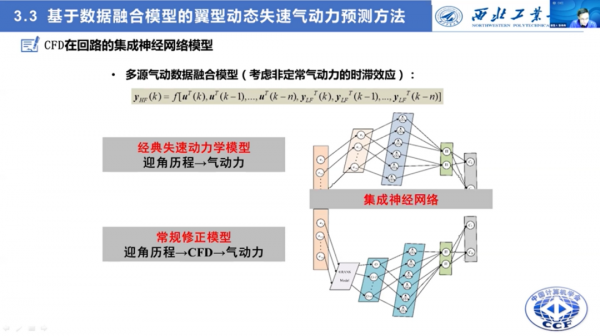
我們對這個模型架構進行了驗證。實驗表明,模型的泛化能力很好,並且隨著樣本數增加,預測精度也會增加。這種融合方法可以將升力係數預測誤差降低3倍、力矩係數誤差降低5倍。
人工智慧為流體力學的發展提供了一種新的研究正規化,而流體力學反過來也為人工智慧的發展提供了一個足夠複雜的研究物件,可以說這是傳統學科和新興學科的交叉融合,相得益彰。

在研究過程中我也總結出幾點心得。第一是要充分利用經典流體力學方法和成果的基礎,再結合人工智慧技術,不能脫離學科的特點和背景。
另外,流體力學是一個“大資料、小樣本”客觀環境下的機器學習和建模問題。
最後,在未來發展方向上,我們可以探索智慧流體力學的可解釋性,也包括探索流體力學新的物理內涵和科學認知。
最後,簡要總結一下科學研究的四個正規化。第一正規化,觀測和實驗,比如說開普勒定律的發現中扮演重要的角色。第二正規化,理論科學正規化依然很重要,這在流體力學中包括流動定律、流體力學的N-S方程等等。第三正規化,計算科學,也包括理論模型、分子動力學,流體力學的CFD就是一個典型的第三正規化研究。本報告涉及的主要是第四正規化的研究。但我們也要看到,流體力學問題不光是一個大資料驅動的科學,還需要將四個正規化進行一個有機的融合。

我們現在做的很多工作,特別是效果比較好的一些模型,恰恰是各種手段的有機結合。
比如對於載荷的一些稀疏重構,就是從計算中提取特徵,以利用實驗觀測值對實驗資料進行精細化重構。
驅動力的變精度模型也是在神經網路架構下,對計算結果和實驗結果進行有機的融合。
近年流體力學研究中的數值同化也是從第三正規化和第一正規化即實驗觀測值的一個結合。
動態失速預測使用的整合模型融合了實驗資料、理論模型以及神經網路的架構,也是在這三種正規化有機結合下開展的工作。
而最近計算物理領域比較火熱的物理約束神經網路,它就是神經網路架構下把數值方法和控制方程緊密地耦合到一起。
如果再融入實驗資料的話,就是四個正規化的有機結合。我們最近開展的工作是基於實驗資料同化的湍流機器學習手段,正好是四個正規化的有機結合。這個方法有實驗資料,也有N-S方程,還包括數值求解,此外又是在神經網路架構下對湍流模型的最佳化。是四個研究正規化融合研究的典範。
參考文獻
1.張偉偉,寇家慶,劉溢浪.智慧賦能流體力學展望[J].航空學報,2021,42(04):26-71.
2.Zhu L, Zhang W, Kou J, et al. Machine learning methods for turbulence modeling in subsonic flows around airfoils[J]. Physics of Fluids, 2019, 31(1): 015105.
3.Kou J, Zhang W, Data-driven modeling for unsteady aerodynamics and aeroelasticity, Progress in Aerospace Sciences, 2021, 125: 100725
4.Zhu L, Zhang W, Sun X, et al. Turbulence closure for high Reynolds number airfoil flows by deep neural networks[J]. Aerospace Science and Technology, 2021, 110: 106452.
5.Wang X, Kou J, and Zhang W, A new dynamic stall prediction framework based on symbiosis of experimental and simulation data, Physics of Fluids, 2021, 33, 127119.