作者|胡竭末
編輯|Trader Joe's
對稱性在現代物理中佔據核心地位,而描述對稱性最有力的工具就是群論。
在本文我們將簡單介紹一種特殊的群——李群。
物理上經常會遇到一些能連續變化的對稱性,為了描述這種連續變化的對稱,我們就要藉助李群。
比如洛倫茲對稱性就是這樣一種對稱性,藉助李群(及它的表示論)的概念,我們可以定量地描述洛倫茲變換甚至由此匯出自旋的概念。
另一方面,現代粒子物理有一個很重要的思想那就是理論告訴我們實驗能看到什麼,這當然不是說理論可以瞎編而不用對實驗結果負責,應該來說這句話是指只有透過理論才能賦予實驗資料意義。
從這點上講,我們如今所談的“粒子”這個概念其實是指“李群的不可約表示空間的基”這樣一個東西。
因此即便不進行定量運算,僅僅是從概念上了解現代粒子物理也需要李群的知識。
更進一步的,目前人類最準確的物理理論——標準模型,它本質是一個規範理論,而這個規範理論的核心要素規範群就是一個李群。
總之,物理學家能不用的數學一定是不用的,而李群李代數如此廣泛地出現在物理理論中說明現代粒子物理真的離不開它。
本文的目的是簡單介紹李群李代數:
- 第一節我們回顧群的基本定義
- 第二節給出李群的定義
- 第三節介紹李代數以及它和李群的關係
一、群和對稱
對稱是一個極其常見的概念,但是數學上如何準確地描述這個概念卻不是一個簡單的問題。
為了精確地描述這個概念,我們先訴諸於直觀。
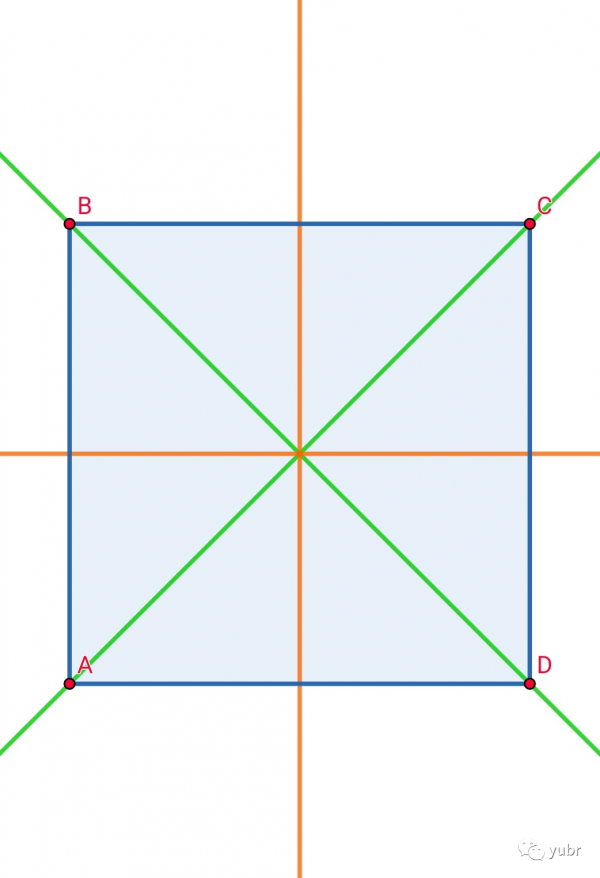
考慮一個正方形,我們會說它沿對角線或者中線(兩條對邊中點的連線)對稱,原因是沿線兩邊“長得一樣”。
如果這時候我們把它沿對稱軸翻轉,那麼由於左右兩邊長得一樣,因此我們看不出翻轉操作前後這兩個正方形有什麼不同,既然如此,我們就可以說在這個操作下正方形是不變的。
如果我們繼續沿先前的對稱軸翻轉,很明顯正方形還是不變,對於同樣的操作(沿先前的對稱軸翻轉)無論我們翻轉多少次,正方形都是不變的。
現在我們可以對對稱下一個定義:
某個操作保持被操作物件不變,那麼我們稱這是一個對稱操作。
有的時候也會說這個物件具有相應操作的對稱性。
理清楚了對稱指什麼,我們現在需要找到某個理論來描述它,這個理論就是群論。
先給出群的定義
設一個集合,集合內的任意兩個元素間,存在這樣一個二元運算
1.封閉性
即任意兩個元素的運算結果仍然在這個集合內。
2.結合律
3.存在唯一單位元
4.集合中任意元素存在唯一逆元
那麼我們就說這個集合和二元運算構成了一個群。
對於正方形的對稱變換一共有8個元素,分別是:
恆等變換,順時針旋轉,順時針旋轉,順時針旋轉,沿四個對稱軸的翻折。
很容易可以驗證它們滿足群的定義,習慣上我們稱這個群為。
另一個例子是所有的整數和加法操作構成一個群,稱為加法群。
只有有限個群元,加法群則有無限個。
為什麼說群對應了對稱呢?
我們可以想象既然對稱操作不改變物件,那麼無論什麼樣的對稱操作相繼加在物件上也仍然是對稱操作,同時總有一個恆等操作——什麼也不操作。
而對於存在逆操作的要求也是非常自然的(事實上,對於僅不滿足群定義4的集合,我們稱它為(么)半群,現代物理裡非常重要的重整化群就是半群。)。
如此對照,我們就發現對稱操作通常自然地擁有群結構,因此,我們可以用群論來研究它。
二、李群
我們已經知道了群可以對應到正方形的對稱變換,那麼一個圓的對稱群是怎麼樣的呢?
直觀上我們會認為圓比正方形更對稱,因為以圓心為旋轉軸,旋轉任意角度,圓都保持不變,所以我們可以說有無數個對稱操作。那麼對應的群也應該包含無數個群元。
有無限群元的群並不是什麼奇怪的情況,我們熟悉的加法群就有無限個群元。
但是對於圓的對稱操作似乎還有什麼不同於加法群這種無限群的地方,這是什麼呢?
答案就是當我們說到圓的變換時,我們可以談圓轉了一個無窮小的角度。對於群這個代數結構來說並不能體現“無窮小”這個概念,因為無窮小涉及到極限,而極限的概念依賴於拓撲而非群。
所以我們需要同時用到群結構和拓撲結構才可以準確的說明這種變換。
在實際應用中,我們通常不僅需要拓撲結構,還需要建立在拓撲上的微分結構,這兩者結合就引出了李群的概念。定義
一個李群為一個集合,滿足
1.是個群
2.是個微分流形
3.的群結構和微分結構相容。
一般來說我們會將每一個群元對應到流形上一點,並且把單位元置於原點處。相容性條件告訴我們群運算
1)
可以寫成流形上的一個二元對映
並且對映是光滑的。
2), 存在 滿足
。
李群同時具有群結構和微分結構,這使得我們可以同時用群和流形的方法去研究它。
我們來看幾個例子
1.矩陣群
一維么正群是滿足的群。我們可以把它直接寫出來,
所以它所對應的流形就是圓。
2.矩陣群
二維么正群是滿足的群。如果我們要求它的矩陣表示還滿足,那麼我們稱這個子群為矩陣群。
它的群元滿足
因此
所以只有3個獨立的實引數,可以寫成
約束條件告訴我們,這是一個三維球面。
三、李代數
現在讓我們看看同時用群和流形的手段可以得到些什麼。
對於微分流形,我們知道可以在上面有切向量。
現在考慮在原點處的一個切向量,由於李群的每一個元素同時還是一個群元,所以任何群元都可以作用到原點。
這樣一個群作用是一個光滑對映,那麼我們可以問這個對映對切向量有什麼影響?
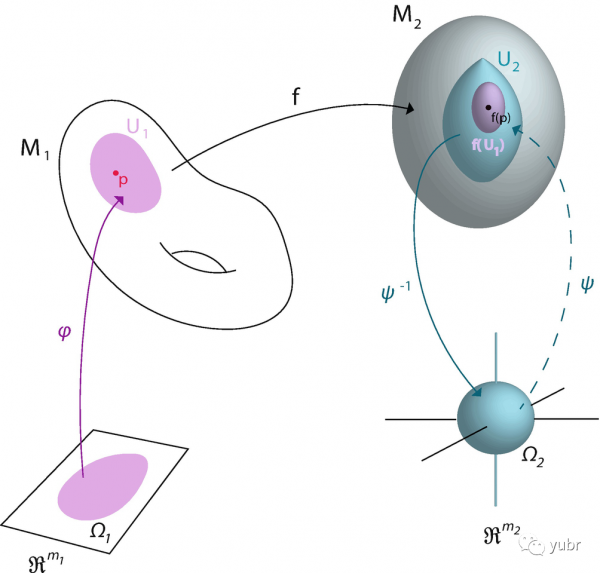
由微分流形的知識我們可知,任何一個對流形的光滑對映
都可以生成一個對切向量的推前對映,
因此群元就伴隨著這麼一個推前對映,從而把原點處的切向量映到點處的某個切向量(注意,之所以這樣是因為我們把原點設成了單位元,所以作用到原點結果為點。)。
我們用這種方式將所有的群元都作用到切向量上,從而可一個切向量場。
這個切向量場有一個非常特殊的性質,那就是群作用對它保持不變,因此我們把它叫做(左)不變向量場。下面給出簡單的證明
設這個向量場在任意點的向量為,由上面的構造我們知道,這個是從原點處做推前對映而來的
由於群運算,我們知道,因此
所以群作用不改變我們構造的切向量場,證畢。
對於任何的位於原點處的切向量,我們可以用這種方法構造向量場。對於向量場,可以求它們的李導數
我們把求得的李導數在原點處的值記為,這樣一來就可以定義一個新的原點處切空間中的二元運算
可以證明這個新的運算還滿足分配率
我們把這樣的新的一個代數關係稱為李群的李代數。
數學上李代數並不依賴於李群而存在,我們完全可以脫離李群單獨學習使用李代數。不過物理上一般李群和李代數都是結合在一起的,因此我們接下來簡單聊聊李群和李代數的關係。
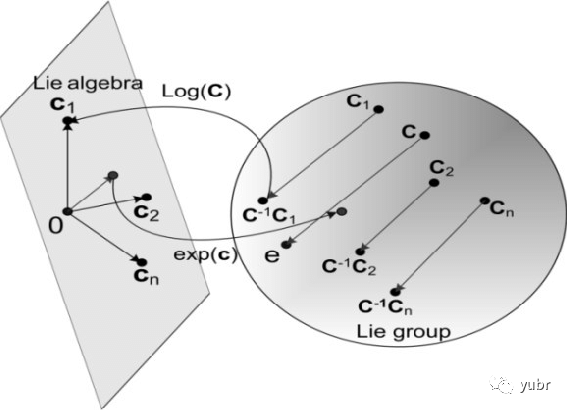
從構造李代數的過程中我們可以看到,李代數可以在區域性轉變為李群元素,因為李代數可以看成是李群單位元上的一個切向量,所以這個切向量可以生成一個區域性的流滿足
解出這個流,我們發現結果是一個指數對映
由此知道了原點附近這一條曲線上的元素了,取不同的切向量,就得到不同方向的流,從而可解出原點附近所有的元素。
不過這種方法一般來說不能得到李群的所有元素,只有緊緻連通李群指數對映才是滿射。
有時我們也會把叫做生成元,當我們把叫做生成元時,強調的是它的李代數性質而非流形上的切向量。
李代數把處理李群這樣一個非線性的物件轉變成了自身這種線性空間,這大大方便了很多問題,不過李代數只能反映李群的區域性性質,對於整體性質則無能為力,事實上不同的李群可以有相同的李代數,因此對李群的研究也不能僅藉助李代數。
轉載內容僅代表作者觀點
不代表中科院物理所立場
來源:yubr
編輯:牧魚