假如有生活在面上的二維生物,那麼他們如何知道自己所處的面是平面還是曲面?
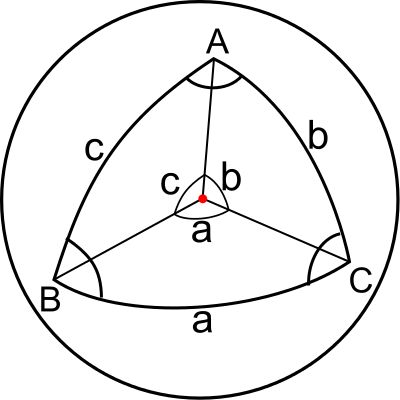
我們從數學上可以知道,在平面中三角形的內角和等於180度;而在曲面中,三角形的內角和可以不等於180度。利用這個數學知識,他們可以知道自己所處的面是平面還是曲面。有的人還知道,把一個向量沿封閉路徑平移一週,如果新向量能和原向量重疊,那麼這個面就是平面;如果二者之間差了一個角度,那麼這個面就是曲面。
但是,如果不仔細思考而簡單地實施這些方法,我們會發現得到了錯誤的結論。以我們的地球為例,我們知道地球表面是一個球面,但是我們平時所見到的卻是平坦的,如果我們在這上面畫三角形,我們也會發現它的內角和為180度。如果按照上述方法,我們應該得到我們所生活的表面是一個平面而不是球面。
人的渺小對比地球之大,我們所生活的表面確實可以看成是曲率為0的平面,但這離真相還相差十萬八千里。為了更好地利用上述數學知識來揭開真相,我們需要避免讓三角形只存在於局域之中,而是儘量讓它處於全域性之中,這樣才能發現三角形的內角和並不等於180度,我們所生活的表面是曲率不等於0的曲面。二維生物也要注意到這個細節,他們才能得出真相。
同理,我們想要測量出宇宙是平坦的還是彎曲的,也不能侷限於某個區域。除了我們剛才所講的這種局域的效應之外,質量的存在也會彎曲周圍的區域性空間,造成測量出的結果更不準確。因此,科學家在測量宇宙的形狀時,會使用更廣闊的宇宙空間。
事實上,空間除了彎曲之外,還可以扭曲。彎曲用曲率來表示,扭曲用撓率來表示。如下圖所示,有OQ和OQ'兩個向量,它們分別沿著對方的方向平移,如果空間存在扭曲,則平移後的P點和P'點並不會重疊在一起。
在廣義相對論中,一般不考慮撓率的存在,因為這會使問題變得更加複雜,而且得出的結論在實際觀測中也沒有出現。