AI for Science領域存在大量未解NP-hard問題,其中就包括量子多體問題。
作者丨何力新
整理 | Don
編輯 | 青暮
人工智慧的下一個目標是從模仿認知學習,轉向解決一直存在的大規模科學計算問題,UC伯克利教授Michael Jordan曾經強調。而李國傑院士也曾在與雷峰網的交流中進一步指出,人工智慧應該突破約翰·麥肯錫和艾倫·圖靈定下來的框框,去研究NP-hard級別的大難題,讓基礎科研走向大工程化。也就是說,要用資料、算力和演算法合力去尋找這類難題的具體解,並落地應用,而不僅僅追求理論邊界的證明。
這些具有組合爆炸性特點的難題很早就已存在,並且有非常顯式的定義,但依然由於計算難題被卡住。而人工智慧特別是深度學習在層級特徵建模、壓縮表徵等方面的優勢,為解決這類問題帶來了新的曙光。AlphaFold是其中的絕佳範例,再往上一層看,在整個AI for Science領域中,比如物理、化學、生物等都存在大量的未解決NP-hard問題,其中就包括了物理學中的量子多體問題。
比如,確定量子混合態是否存在糾纏就是一個NP-hard問題。k-Local Hamiltonian 問題(k-LH)至少是NP-hard問題。它們都涉及量子多體系統。
k-LH問題是指:給定k,在n個量子位元的系統中,存在一組約束,每個約束最多涉及k個量子位元,希望確定系統的基態能量是高於某個閾值或低於某個閾值。它屬於一種量子多體問題,並且k不小於2時,至少是NP-hard的。當k=3或以上時,甚至出現了更高階的複雜性類——QMA完全。
QMA類似於經典複雜性類中的NP,也就是說,如果一個問題的答案可以在量子計算機上以多項式時間驗證(並且至少有2/3的機率是正確的),但無法以多項式時間給出答案,則該問題的複雜性類為QMA。同樣,QMA完全也類似於NP完全。
多年以來,量子多體物理領域是凝聚態物理中最核心和最優挑戰性的話題之一。比如物理世界中我們能夠觀測到的一些奇特物理現象和物質中,最具代表性的便是超導、超固量子Hall效應、超流、玻色-愛因斯坦凝聚和量子自旋液體等,都是基於大量粒子相互作用的量子現象。
著名的物理學家Phlips Anderson曾說,“More is Different”,這是指我們的世界並非各個物質的簡單疊加,當系統中的粒子數以及元素種類增多的時候,會導致1+1>2的效果。從理論上來說就是量子多體之間的相互作用所致的結果。
由於希爾伯特空間隨著粒子數增加而指數增長(組合爆炸),量子多體問題的高精度模擬是對於經典計算機極富挑戰性的問題。近幾年發展起來的深度學習演算法為模擬量子多體提供了新的有效的計算工具。
2021年12月16日,中國科技大學物理系教授何力新在CNCC 2021“人工智慧在超大規模科學計算領域的應用探索”專題論壇上做了題為《深度學習演算法在新一代神威超算平臺的應用:量子多體問題模擬》的學術報告,分享了深度學習演算法在量子多體模擬問題上的研究工作和領域進展。
在報告中,何力新表示,他們團隊設計了基於卷積神經網路的新演算法,對強阻挫的強關聯自旋系統實現了高精度的基態模擬。他們還在新一代神威超級計算機上移植並優化了該演算法,並計算了著名的方格J1-J2模型,將計算的系統規模及計算精度提高到了新的高度。在移植、最佳化程式的過程中,透過物理學-並行最佳化-超算系統三方面交叉團隊,成功在新一代神威超算上實現高效能的量子多體問題模擬,為構建國產AI-HPC生態提供一個優秀的模板示例。

何力新教授是中國科技大學物理系教授,1997年畢業於中國科技大學,2003年在美國羅格斯大學攻讀博士,2003~2006年在美國國家再生能源實驗室從事量子點的理論研究工作,並於2006年回國到中科大中科院量子資訊中心進行研究工作,2011年獲得傑青稱號,2012年入選IOP Fellow,曾任科技部量子調控量子通訊網路和量子模擬關鍵器件物理實現之首席科學家。
以下是演講全文,AI科技評論進行了不改變原意的整理:
1 量子多體問題及其模型

研究量子多體問題具有極強的科學意義,可以從兩個方面進行概括。首先在基礎研究的角度上來看,量子多體問題的一個主要目標是發現和研究新的物質形態。我們可能對生活中常見的固體、液體和氣體形式十分熟悉,但其實自然界中有很多其他物質形態,比如我們之前所說的超導和量子自旋液體等,這些新型的物理形態都具有各自的存在意義以及研究價值。
因此透過對新型物質形態的研究,我們便可以洞悉和總結物理世界的深層規律和法則。
另一項具有意義的方向是研究其應用價值。例如高溫超導已經在能源、交通、精密測量和資訊等領域有了廣泛的應用。托克馬克裝置需要非常強的磁場進行物理約束,因此可以利用超導體產生超強的磁場。此外,拓撲序也可以進行拓撲量子計算。

在量子多體物理的模型中,有兩個經典模型,即海森堡自旋模型,以及哈伯德電子模型。其中海森堡模型其本質是一個自旋模型,它描述了格點上兩個自旋量子的相互作用。比如圖中描述了兩個最近鄰的兩個量子發生的交換作用J,如果J>0,則兩個粒子傾向於自旋反平行。但是當J<0時,粒子傾向於自旋平行。
另一個經典模型是哈伯德模型,它描述了電子運動的模型。該模型描述了量子在格點上的運動,其中第一項表示的是電子從一個格點跳躍到另一個格點的過程。第二項,描述的是同一格點上電子的庫侖排斥作用。
從區域性的角度來看,這兩種模型很容易理解。但是當粒子數逐漸增加的時候,系統將變得十分複雜,對其求解將會變得十分困難,算力需求也難以滿足。
2 多體模型計算的困難性

計算困難的根本原因在於量子態的希爾伯特空間會隨著粒子數量的增加而呈現指數級的增長。比如有N個1/2的自旋粒子,每個自旋有上下兩個狀態,那麼態空間將達到2^N級別。因此如果我們需要對其進行嚴格求解,會遇到“指數牆”的問題,也就是算力需求巨大。目前我們只能實現大約40個格點的自旋系統的嚴格求解。
此外,我們也有一些其它近似方法,例如量子蒙特卡洛方法。但是它在計算費米系統(電子系統)和阻挫系統時會出現符號問題,即負機率問題。而動力學平均場方法,會對一維和二維等低維度的模型有計算問題。最後是密度矩陣重整化方法,只能計算一維和準一維的問題。

在過去的十幾年間,國際上發展了一些新的演算法,例如張量網路態方法(PEPS演算法)。這些演算法將量子態表示為格點上的張量乘積形式。原則上這種方法可以在一定程度上克服已有方法的不足,它可以應用於二維繫統,也不存在對阻挫系統和費米系統中的符號問題。
但是另一方面,它的計算複雜度很高,尤其是對週期性邊界條件的問題。因此我們目前無法對具有周期性邊界條件的系統進行有效的模擬。

在2018年,我們曾經在神威機器上進行了PEPS演算法的實現和模擬。當時可以將演算法的並行度做到1000萬核。我們可以看到之前工作的演算法精度僅能達到10-3,但是神威機上的PEPS演算法則將精度是提高了2個量級。但是這個演算法仍舊僅適用於開放邊界條件的問題。
3 量子力學遇見人工智慧

我們知道在AlphaGo在擊敗人類圍棋玩家之後,深度學習大熱,引起了很多領域的改革。實際上,深度學習在凝聚態物理學中也掀起了一番熱烈討論和嘗試。它可以做實驗資料的處理,可以進行機器學習勢場模型的模擬和求解,也有工作研究了用AI進行分子和晶體結構的分類和預測,進行電子密度的學習等。近些年DeepMind的最新工作就是在這些方面進行研究和發現,比如使用神經網路估計電荷的密度,並且超越了人類的估計結果。

大家也在嘗試將深度學習和機器學習用在量子多體問題中。上圖是2017年的一篇Science工作,它使用受限玻爾茲曼機模型研究海森堡自旋模型,將系統的粒子波函式利用玻爾茲曼機進行表示和學習,透過最佳化系統的能量,得到神經網路的最佳引數。
在量子多體系統中,演算法的好壞判斷標準是計算的能量是否最優。從結果中我們看到,該計算能量的精度已經到達10-3量級,甚至超過了(我們神威工作)之前PEPS的演算法效果。
但是該神經網路也面臨一些問題,它只能描述簡單的物理模型,無法模擬具有競爭相互作用的物理系統。
4 人工智慧的多體問題挑戰

那麼什麼是相互競爭作用呢?我們結合這裡的模型進行解釋。J1-J2模型是一個典型的具有競爭相互作用的自旋模型。我們看到圖中每個格點上有一個自旋,它們與近鄰的自旋有相互作用,其中J1描述兩個最近臨的格點上的自旋相互作用,J2則描述了兩個次近鄰格點上自旋的相互作用,也就是對角線上的相互作用。如果相互作用的J大於0,則意味著這兩個格點的自旋都傾向反平行。當J1, J2 都大於0時就會出現問題,即如果近鄰格點是反平行,那麼次近鄰格點就一定是平行的,這就和J2相互作用的要求矛盾。該種帶有競爭相互作用的系統被稱為阻挫系統。
打個比方,一個員工可能有兩個老闆,其中一個老闆要求你向東走,另一個要求向西走。則此時會產生矛盾(Frustrated Interaction)。當然,如果其中一個老闆很強勢,我們跟著強勢的走。但是如果兩個老闆勢均力敵,你就會很迷茫。
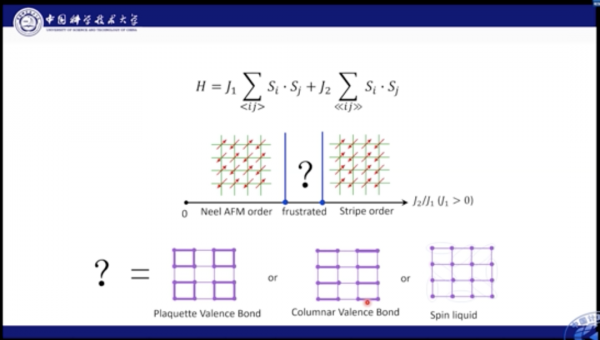
對J1-J2模型也是如此,如果J1較為強勢,那麼系統中的自旋會傾向於做出棋盤形狀的持續排列。如果J2更強勢,自旋則會沿對角線進行反平行排列。當兩者相互作用效果相近時,則會產生更多豐富的物理現象。
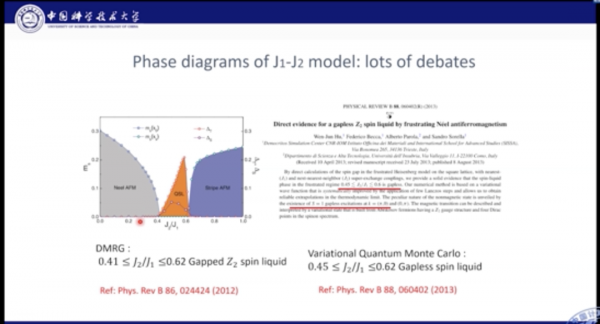
J1-J2模型十分經典,人們對其基態進行了長期的研究。目前針對J1較強,以及J2較強的情況研究已經較為清晰的結論,但是對於J1-J2共同作用的中間區域,一直存在爭議。

對於該區域的基態,人們有幾種不同的看法。比如,有人認為格點可以形成Plaguette態,Plaguette態是一個規則有序的態;此外,也可能會形成Columnar態;也有人提出,可能其中就是一種混亂無序的狀態,即自旋液體態。自旋液體態十分複雜,有著非常複雜的量子糾纏和奇異量子行為。Philip Anderson認為量子自旋液體是研究高溫超導的關鍵問題之一。
5 深度學習和量子多體

之前的玻爾茲曼機模型是無法很好地模擬該場景的。在該方法中,它將波函式視作所有可能自旋結構的疊加,其中W(S)就是自旋構型的權重,該權重在海森堡模型中都是>0的,但是在有競爭的模型中正負都有可能。因此在玻爾茲曼機模型中,就無法處理此類同時具有正負情況的波函式。
為此,我們提出使用深度卷積神經網路來描述波函式。我們的網路包括了很多Building Block,每個Block又分為多種運算元,包括卷積、Max pooling和反捲積等。
當我們輸入一個自旋構型,該網路可以給出有正有負的構型權重,此時的引數量是隨格點數量線性增長,而非災難的指數形增長,這就意味著我們的神經網路可以使用有限擴增的引數量來模擬出系統中指數增長的Hilbert空間。當然這個空間也是僅在基態附近的部分。

當我們確定了神經網路的結構來模擬波函式後,重要的是需要獲得系統的基態,所謂基態是指系統的能量最低態。也就是我們需要透過神經網路求解系統能量最低態的引數。
這裡的能量可以表示成所有自旋構型加權求和的形式,因此可以使用馬爾可夫抽樣的方式進行求解。這是一個典型的強化學習場景,我們可以透過最佳化系統能量來得到網路引數。
但是這個模型和一般的機器學習演算法有所差異。第一,它需要極高的精度,我們需要比其他方法要求高至少2個量級的精度。其原因是量子態的求解精度需求極高,微小的誤差將對基態解產生巨大影響。此外,系統中可能存在多個區域性最優點,若我們用普通方法進行最佳化,則可能陷入局域極值中。
為了解決這個問題,我們使用SR方法進行解決。在機器學習中我們常稱之為自然梯度法。為了更新網路引數,我們需要求解能量對引數的多個梯度,為了計算梯度相,我們需要進行求導,並求解關聯矩陣的預處理,加速收斂。

這裡的計算熱點包括馬爾可夫取樣。因為我們需要計算關聯矩陣,需要50萬sweep的自旋樣本,每個sweep都需要對所有網格進行翻轉。但是在sweep之間是不需要進行求導和反向傳播的,我們只需要正向執行,並在全部sweep做完後進行反向傳播,以此降低通訊時間佔比,以及計算量。
另一個計算熱點是SR最佳化方法。在SR演算法中一個重要步驟是計算大的關聯矩陣,然後求解線性方程組。具體哪部分的耗時是最嚴重的,其實是由模型引數大小所決定的。如果系統越大,取樣越耗時,引數越多,SR方法的耗時越大。
6 實際效果

我們分別在自己的機器以及新一代的神威機上進行了驗證和部署。神威機具有異構的結構,其NPI處於核組之間,因此有64個組合。在核組級別上的並行本質是執行緒並行。神威機的異構結構很適合此類應用,因此為了最大化利用神威機的能力,我們針對神威機的特點和應用特點設計了雙層並行方案。首先在核組之間的並行被用作自旋取樣,即每個自旋部署在不同的核組之上進行獨立取樣。在求解線性方程組的時候,會使用ScaLAPACK進行計算劃分。在並行內部,我們使用卷積運算元從核加速,並利用網路輸出時採用批次>1的計算,將從核的計算效能妥善利用。
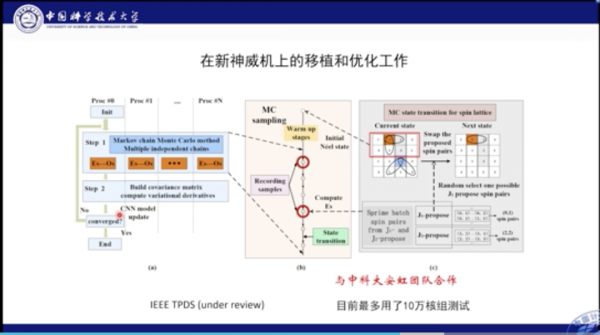
這是我們的程式在新的神威機上的移植和最佳化的示意圖全覽。可以看到在不同的核組之間我們進行了單獨獨立的取樣;取樣後將其收集並計算關聯矩陣,並求導更新引數。這項工作最大利用了10萬核組測試。

在效能表現方面,我們對比各個主機的用時結果。從上圖中我們可以看到,我們分別比較了16000個引數,和10萬個引數的場景。不論引數量如何,其主要的計算時間還是集中在前向計算部分,SR最佳化的佔比只有1/4左右。
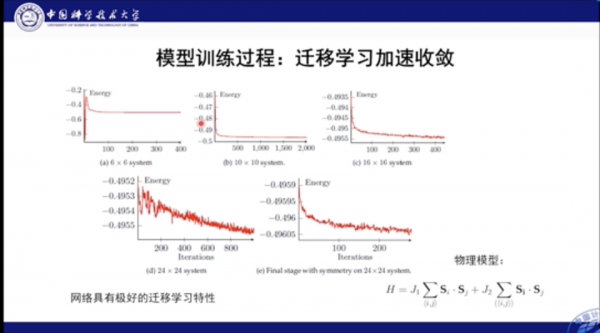
本工作的另一個優點在於其可遷移性極高。我們首先可以在較小的神經網路中進行學習,而後將其擴充套件到體積大的網路中。在實踐中,遷移後通常只需要幾百步便可以使大網路收斂,這無疑加速了模型的訓練和應用。

這裡我們對比了效能。綠色和棕色線都是直接學習的結果,藍色和紅色是遷移的結果。透過圖中結果我們知道,如果使用直接學習,則網路很難收斂到最佳結果,而遷移則極大加快了這個最最佳化的過程。


我們也分析了基態能量部分的外推結果,經過計算發現,能量在網格達到24×24後便逐漸收斂,我們也對多種磁序進行外推,比如Dimer序和反鐵磁序。結果發現,系統在中間區域的基態是自旋液體相。

與之前的最佳結果對比,我們的優勢在於,網路的擴充套件性更高,也就是可以處理的系統尺寸更大,具有極好的遷移學習特徵。
在下一步工作中,我們將繼續進行相關研究,主要最佳化卷積運算元的效能,提高神經網路的計算速度;最佳化ScaLAPACK庫,提升最佳化演算法的速度;增加網路引數,得到精度更高的基態。
該模型可以進一步拓展到其他種類模型上,比如三角格子、六角格子和kagome格子等場景。我們還可以在近鄰、次近鄰作用的基礎上新增次次近鄰的相互作用。這些物理模型都有其特殊物理現象。
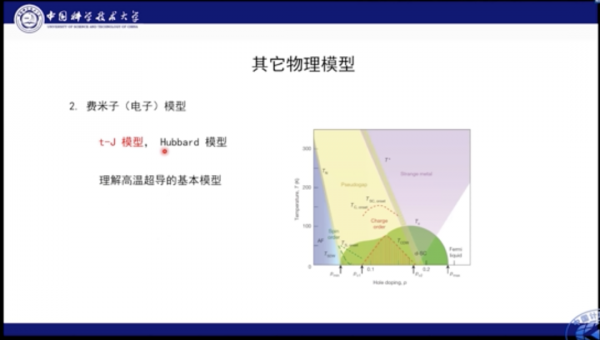
該模型還能用在費米子(電子)模型比如t-J模型上,我們初步的測試目前來看效果很好。
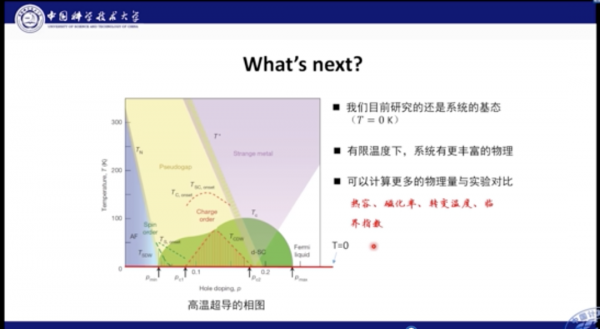
但是當前我們的研究還是限於系統的基態,即T=0K的場景。而真正有限溫度下的系統,可能存在更豐富的物理系統屬性,可以計算更多的物理量和實驗進行對比。

有限溫度的研究是個極大挑戰。因為絕對零度場景下系統處於基態,因此可以使用波函式進行描述。但是當溫度不等於零時,系統處於混態,就必須使用密度矩陣進行描述。此時樣本空間將會成倍的增加,因此需要更多的網路引數,甚至到達100萬左右的級別。