帶電粒子在勻強磁場中的運動（十五）——多解問題（二）

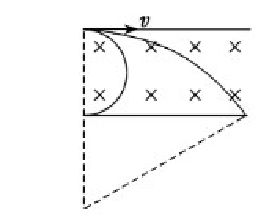
造成帶電粒子在勻強磁場中運動多解問題的因素還有磁場方向的不確定。因為磁感應強度是向量，如果題述條件只給出磁感應強度大小，而未說明磁感應強度方向，則應考慮因磁場方向不確定而導致的多解。 如圖所示，帶正電粒子以速率v垂直進入勻強磁場，若B垂直紙面向裡，其軌跡為a，若B垂直紙面向外，其軌跡為b。

還是拿一道例題來說：一質量為m，電荷量為q的負電荷在磁感應強度為B的勻強磁場中繞固定的正電荷沿固定的光滑軌道做勻速圓周運動，若磁場方向垂直於它的運動平面，且作用在負電荷的電場力恰好是磁場力的三倍，則負電荷做圓周運動的角速度可能是( )

解析：還是需要我們仔細審題，明白題目到底想考什麼，依題中條件“磁場方向垂直於它的運動平面”，磁場方向有兩種可能，要麼垂直向上，要麼垂直向下，且這兩種可能方向相反。在方向相反的兩個勻強磁場中，由左手定則可知負電荷所受的洛倫茲力的方向也是相反的。

當負電荷所受的洛倫茲力與電場力方向相同時，根據牛頓第二定律和圓周運動的相關知識，可知4qvB＝mv²/R，得v＝4BqR/m，此種情況下，負電荷運動的角速度為ω＝v/R＝4Bqm；當負電荷所受的洛倫茲力與電場力方向相反時，有2qvB＝mv²/R，v＝2BqR/m，此種情況下，負電荷運動的角速度為ω＝v/R＝2Bqm。

反思：做這道題是不是需要溫習一下合力充當向心力，向心力的計算方法你忘了嗎？洛倫茲力的計算方法你還記得嗎？

如果你有今日頭條app，麻煩順手點一下關注@中學物理知識傳播者，每天都會傾情奉獻一段小乾貨，我會繼續努力的！