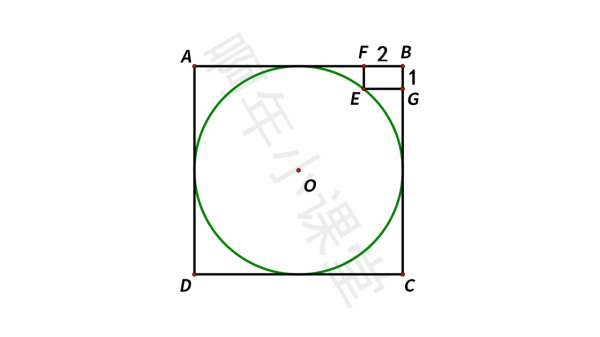
如圖,已知四邊形ABCD是正方形,圓O與正方形ABCD的四條邊相切,四邊形BFEG是矩形,BF=2,BG=1,求圓O的面積。這道題怎麼做呢?
我們要求圓O的面積,就需要知道圓O的半徑為多少。對於這種題目,很多時候我們都是找直角三角形,透過勾股定理去構造方程,從而求出圓的半徑。這個方法是常規操作,找直角三角形,構造方程。
從圖中可以看到,點E落在圓上,我們不妨將OE連線起來,接著將點O和AB上的切點連線起來。根據切線的性質,OM⊥AB。
之後過點E作OM的垂線。
如圖所示,EN⊥OM。三角形OEN是直角三角形。
假設圓的半徑為r,則OE=r,ON=OM-MN=r-1,NE=NG-EG=r-2。
由勾股定理,可得OE²=ON²+NE²,即r²=(r-1)²+(r-2)²,解得r₁=1(捨去,顯然r>1),r₂=5。
所以圓的面積=πr²=25π。
以上就是這道題的解法,除此之外你還有其他的方法嗎?可以在評論區留言~