我們用LIGO探測引力波，在這種情況下，LIGO那4公里長臂的長度變化小於單個質子寬度的一萬分之一。我們的測量已經變得如此精確，以至於我們開始遇到絕對量子極限，也就是海森堡不確定性原理定義的極限。但無論是物理學家還是工程師，都不會讓基本自然法則阻礙他們。透過這篇文章，我們將看到如何破解不確定性原理，從而使測量變得比以往更加精確。

不確定性原理地提出

海森堡不確定性原理告訴我們，自然界存在著一種基本的不可知性——一種對我們測量宇宙的精確度的絕對限制。該原理提出，存在著一對屬性，我們不可能同時精確地知道：對粒子位置的完全瞭解意味著它的動量是不確定的；而對它能量的精確測量意味著它在時間上的位置在量子力學中是模糊的。在量子力學中，我們將這些屬性對稱為互補變數。不確定性原理告訴我們，當我們將這些屬性對相乘時，它一定總是大於某個特定的但特別小的數字。

1920年代，海森堡在發明他的矩陣力學時就發現了測不準原理。但是，當海森堡第一次提出這種關係時，他並沒有意識到這個原理是如此基本的，當時他考慮的是用光子測量粒子的位置會發生什麼。他推斷光子會給粒子一個動量衝擊，這就解釋了測量後其動量的更大不確定性。為了更精確地測量位置，將需要一個更高能量的光子，但是它會把被測量粒子踢得更遠，導致動量的不確定性變得更大。基本上，他認為測不準原理的產生是由於測量干擾了系統。

海森堡把他的新想法告訴了他的導師尼爾斯·玻爾。玻爾對這一發現感到興奮，但強烈反對海森堡的解釋，他認為不確定性原理暗示了一個更為基本的宇宙法則。

海森堡的不確定性原理使我們無法同時瞭解有關量子態的所有資訊，但有時我們也可以超越海森堡的極限，因為有時我們更關心的只有其中一個屬性。不確定性原理對互補性質的不確定性乘積設定了一個下限，如果我們只關心粒子的位置，原則上我們可以非常精確地測量它，只要我們不知道它的動量而已。但是，這並不是一件簡單的事情，因為正常的量子態傾向於在互補的屬性之間均勻地分擔不確定性。在過去的幾十年裡，我們開發了理論和技巧，使我們能夠操縱量子態來突破不確定性原理的極限，我們將以LIGO為例。

LIGO提高探測引力波的精度

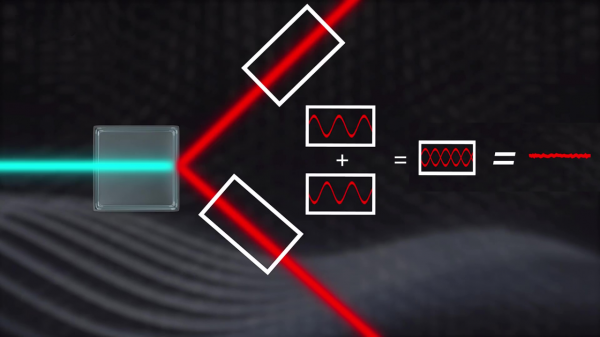
快速回顧一下LIGO的工作原理。位於美國華盛頓州和路易斯安那州的雙干涉儀是由一對4公里長的直角臂組成。鐳射被分裂並沿著這些路徑傳送，然後再以這種方式重新組合，使這些鐳射束的電磁波相消干涉。也就是說，一個波的波峰與另一個波的波谷對齊，導致能量完全抵消。但是，如果引力波透過干涉儀，兩條路徑的相對長度會以一種特殊的方式發生變化，重組的鐳射不再完全抵消，因此我們可以觀察到閃爍訊號。

這種測量方法對路徑長度非常敏感，但這意味著它對光波的相位也很敏感，兩個光束的相對相位的任何變化都會在訊號中產生閃爍。事實上，因為相位存在著固有的不確定性，所以兩個光束的相位從未完美匹配。這會導致低水平的噪音，在應該黑暗的地方出現閃爍的訊號，而這種噪音會掩蓋微弱的引力波訊號。如果鐳射束相位的量子漲落大於引力波引起的臂長變化，那麼我們將永遠看不到引力波，除非我們能破解不確定性原理。

在這種情況下，所討論的互補變數不是位置和動量，而是變成相位和振幅。為了提高我們探測微弱引力波的能力，我們需要減少鐳射束相位的不確定性，這將使我們能夠更完美地排列這些波以減少量子漲落。我們不太關心振幅的不確定性。

在LIGO中，光的相位被壓縮，以增加振幅的不確定性為代價提高了精度。這種相位壓縮是透過量子糾纏來實現的，鐳射透過非線性晶體的特殊材料發射，這種材料將入射光子轉換成成對的光子。這些發出的光子具有糾纏相位，它們的波峰和波谷的位置是相關的。這些光子對被送到干涉儀的不同臂上，當它們重新組合時，它們的相位仍然有量子漲落，但兩束光之間的漲落現在是相關的，所以它們可以更完美地抵消。由於隨機相移導致的閃爍減少，這意味著我們可以看到由更微弱引力波引起的真實訊號。

當然，為了提高相位精度，總是要付出代價的，那就是鐳射束中傳輸的振幅的不確定性。但這也引入了另一種噪聲——輻射壓力噪聲，不過這種噪聲比相位不確定性的問題要小得多。凡事都有代價，但如果你把不確定性投資在正確的地方，這個代價是值得的。

寫在最後

這種壓縮光的使用只是量子力學如何用於提高測量精度的一個例子，科學家們已經在其他系統中證明了同樣的原理，比如糾纏原子鐘，這可能會在某一天大大提高我們北斗衛星的定位精度。我們測量世界的能力是有極限的，但只要我們願意改變一些基本定律（比如不確定性原理），我們就可以將極限推到我們認為可能的範圍之外，從而對這個不確定的時空進行更加確定的測量。