題目如下:
這題其實很容易想到的思路是,將兩個數組合併成一個,再取合併後陣列的中位數,程式碼如下:
class Solution {
// O(m+n)
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length, len3 = len1 + len2;
int[] nums3 = new int[len3];
int point1 = 0, point2 = 0;
for (int i = 0; i < len3; i++) {
if (point1 == len1) {
// nums1遍歷完了,把nums2剩下的直接放進來
if (point2 < len2) {
nums3[i] = nums2[point2++];
continue;
}
}
if (point2 == len2) {
// nums2遍歷完了,把nums1剩下的直接放進來
if (point1 < len1) {
nums3[i] = nums1[point1++];
continue;
}
}
if (nums1[point1] < nums2[point2]) {
nums3[i] = nums1[point1++];
} else {
nums3[i] = nums2[point2++];
}
}
// 取中位數
return (nums3[(len3 - 1) / 2] + nums3[len3 / 2]) / 2d;
}
}很容易就完成了,但是時間複雜度是O(m+n),而且還增加了一個數組的空間,不能滿足題目的要求。題目需要達到O(log(m+n)),那麼就需要用二分法了。
這裡備註一下為什麼二分法的時間複雜度是O(log n),在n個元素中查詢一個數,其剩餘元素的個數依次是n/2¹,n/2²,n/2³···n/2ⁱ,如果第一次就找到了,則時間複雜度為O(1),如果最後剩一個元素的時候才找到,n/2ⁱ=1,i=log n,O(log n)就是這麼來的。
下面來進行二分法,對兩個陣列中較小的一個數組二分,時間複雜度可以降到O(log min(m,n)),具體思路是在nums1中找到合適的位置,對nums1和nums2進行切分:
需要達到的效果可以看程式碼中的註釋,主要是要想到這個思路比較複雜,花了很長時間理解。
class Solution {
// O(log min(m,n))
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
// 保持nums1元素較少
if (nums1.length > nums2.length) {
int[] temp = nums1;
nums1 = nums2;
nums2 = temp;
}
int len1 = nums1.length, len2 = nums2.length;
// 劃中分線的時候,算出左邊元素的個數
// 如果是奇數,讓左邊多一個;如果是偶數,兩邊一樣多
// 比如總數5個和6個,左邊都是3個
int leftCount = (len1 + len2 + 1) / 2;
int l = 0, r = len1;
//
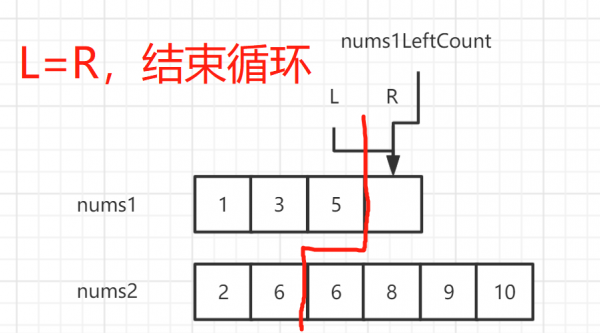
// 核心程式碼在這個迴圈中,對nums1進行二分,左右調整位置找到最後一個小於num2的零界點
while (l < r) {
int nums1LeftCount = (l + r + 1) / 2;
int nums2LeftCount = leftCount - nums1LeftCount;
if (nums1[nums1LeftCount - 1] <= nums2[nums2LeftCount]) {
// 下一次二分的陣列為nums1的nums1LeftCount~r之間
l = nums1LeftCount;
}else {
// 下一次二分的陣列為nums1的l~nums1LeftCount-1之間
r = nums1LeftCount - 1;
}
}
int nums1LeftCount = l;
int nums2LeftCount = leftCount - nums1LeftCount;
int maxLeft, minRight;
// maxLeft一定有
if (nums1LeftCount == 0) {
maxLeft = nums2[nums2LeftCount - 1];
} else if (nums2LeftCount == 0) {
maxLeft = nums1[nums1LeftCount - 1];
} else {
maxLeft = Math.max(nums1[nums1LeftCount - 1], nums2[nums2LeftCount - 1]);
}
// 總數為偶數的時候,中位數為(左邊最大+右邊最小)/2
// 總數為奇數的時候,中位數為左邊最大
if ((len1 + len2) % 2 != 0) {
return maxLeft;
} else {
// minRight不一定有,在總數為偶數的時候minRight則一定有,這個時候再算minRight
if (nums1LeftCount == len1) {
minRight = nums2[nums2LeftCount];
} else if (nums2LeftCount == len2) {
minRight = nums1[nums1LeftCount];
} else {
minRight = Math.min(nums1[nums1LeftCount], nums2[nums2LeftCount]);
}
return (maxLeft + minRight) / 2d;
}
}
}奶思~