我們能造出莫比烏斯環，卻無法造出克萊因瓶，這是為什麼？

現實生活當中，經常有人會將人類和螞蟻做對比，甚至認為螞蟻屬於一種二維生物。這是因為螞蟻的視力很弱，基本是依靠氣味和觸覺判斷方位的，所以螞蟻眼中的世界是二維的，由簡單的點和線構成。但是我們看到的螞蟻明顯是三維的，起碼它們並不是一張紙。針對這類疑惑，科學家們試圖使用幾何讓我們理解各個維度之間的區別，因此特殊的模型出現了，它們就是莫比烏斯環和克萊因瓶。

對於莫比烏斯環，大家肯定都不陌生，畢竟這幾年“莫比烏斯環狀戒指”算得上是熱賣的首飾之一，人們認為它能代表永恆、無限的愛情。它的製作方法很簡單，我們對一張A4紙進行裁剪，剪出一張細長的紙條，將它兩頭抓住扭轉180°，再粘在一起，一個簡易的莫比烏斯環就做好了。可是另一個模型克萊因瓶，卻無法被造出，只能存在於電腦程式建模當中，這又是為什麼呢？原來是因為它並不屬於我們這個三維世界，而是來源於更高的四維空間。

拓撲學

探究莫比烏斯環和克萊因瓶的奧秘之前，我們需要先了解一下它們的來源。其實最初它們都源於數學當中的幾何學，現在已經變成了幾何學的重要分支，改頭換面取了個新名字叫做“拓撲學”。

這門學科最早發展於19世紀，起源則要往前追溯一些，具體可以到18世紀。主要用於研究幾何模型或者空間學的，特殊之處在於拓撲圖形的性質，就是不論你如何將它彎曲、縮小或者變形它都能保持不變，因此還得了一個別稱叫“橡皮幾何學”。

拓撲學研究的圖形會使人感到十分費解，人們不能理解為什麼要研究這些奇怪的圖形。這裡要解釋一下，在我們的慣性思維當中，一切看到的圖形都是在歐幾里得幾何定義之下的，是一種合乎“正常”的模樣。

但是拓撲學則最大程度地跳出了這一定義，幾何圖形或者模型在這裡有著更大的自由度，因此它們看起來奇形怪狀的甚至說更加的抽象，與我們看到的歐幾里得幾何定義下的世界完全不同。因此可以說拓撲學是屬於純粹思維邏輯領域的學說，大家就不要以慣性的思維去看待這些圖形有沒有意義，這是一個思維誤區。

綜合拓撲學的發展以及相關定義來看，這門學科其實更像是一種思維遊戲，絕大多數時間需要依靠大家自行發揮想象力，如果你只是用慣性思維進行看待，那麼確實就是一個非常無厘頭的幾何模型。但是如果大家閉上眼睛進行想象，會發現它不同於傳統數學，有精準的數字或者概念規定，因此拓撲學在現實中的應用其實很少，它更多時候發生在思維層面當中。

下文當中要介紹的莫比烏斯環和克萊因瓶就是拓撲學的典型研究物件，所以希望大家在觀察這兩個圖形的時候，跳脫出直觀世界的限制，不要將重點放在爭論它到底有沒有意義，或者合不合理。

莫比烏斯環是什麼？

莫比烏斯環也可以叫莫比烏斯帶，它是1858年由德國數學家莫比烏斯和約翰·李斯丁共同發現的。它不同於普通紙帶有兩個面，它只有一個面，其邊界由一條閉合曲線組成。假如將一隻螞蟻放在普通的紙條上，螞蟻想到達另一面，肯定需要跨越紙面的“邊界”，但是在莫比烏斯環之上“邊界”神奇地消失了，螞蟻可以不用跨越任何邊緣地帶就抵達另一面，甚至是回到起點。

莫比烏斯環的製作比較簡單，所以這些年來常常出現在大眾視野當中。但是細分之下它還能分為兩種不同的型別，這是由大家扭轉紙帶的方向決定的，向左扭動則得到左旋莫比烏斯環，向右則得到右旋的，不知道商家在製作戒指時會不會注意到這一特點，可以以此來區分男戒和女戒，畢竟剛好與男左女右對應了。

很多人會覺得不就是簡單地扭動了一下，說白了它還是個紙條而已，那麼我們不如來看看莫比烏斯環和普通環圈之間的區別。首先，我們先使用裁剪的方式，看看它們會有什麼不同。將普通紙環沿著中線剪開，那麼你就會得到一個與原來紙環周長相等但是寬度更窄的環。但是如果是將莫比烏斯環沿著線剪開，你得到的紙環周長是原來紙環的一倍，大家有興趣可以剪來試試看。

如果在莫比烏斯圈上劃上兩條等距離線再進行剪裁，那麼你不僅能得到一個比原圈周長長一倍、比原圈寬度窄三分之二的普通環圈，同時還能在其中心部位再得到一個單獨的、比原圈寬度窄三分之二，且周長與原圈等長的“窄”莫比烏斯圈。

可能會有人疑惑這種剪紙實驗確實能證明它與普通的環圈不同，可是除此之外還有什麼用呢？透過上述的裁剪結果可以看出，我們在三維世界當中對它剪裁，竟然是無法將它還原的，而是會剪出新的樣子，這一部分呈現出的是“非三維”的狀態，我們透過外力也無法將其改變。因此可以得出莫比烏斯環實際上是一種非三維的物體，我們能夠將它製作出來完全是因為在這之上套上了兩個三維座標系。

克萊因瓶其實是雙重莫比烏斯環？

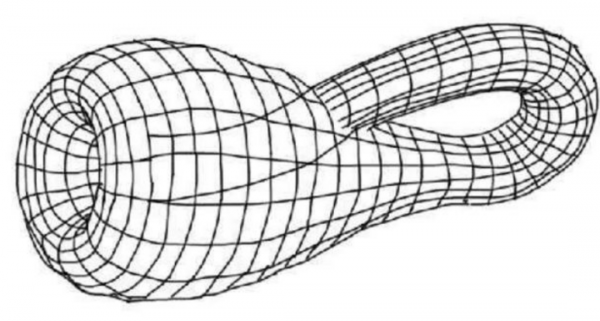
充分了解了莫比烏斯環之後，我們就可以來看看它的升級版“克萊因瓶”了。為什麼這麼說呢，因為數學家已經證明了這兩種模型之間是有聯絡的，在我國數學專家談祥柏先生的著作《數學廣角鏡》當中就明確指出其實克萊因瓶是由兩個莫比烏斯環組合而成的。

克萊因瓶是數學家菲利克斯·克萊因在1882年時發現的，對比上文莫比烏斯環的誕生時間，克萊因瓶要更年輕一些。這個瓶子同樣也沒有邊界，整個表面都是封閉的曲面。大家可能不好想象封閉曲面，其實球體上的曲面就是封閉曲面，假如有人問你地球有邊界嗎？你一定會很糾結，感覺上是有的，但是以球面來說是沒有的。這類無定向性的平面，並沒有內部和外部的區別。

這個瓶子看起來沒有瓶底，瓶頸則被拉長了，看起來是穿過了瓶壁與瓶底連線在了一起，但是如果在電腦建模當中它是沒有穿過的。假如我們將莫比烏斯環上的螞蟻放在克萊因瓶上，那麼它能夠穿過瓶頸，由瓶子的外部爬到瓶子的裡面。不過我們都知道克萊因瓶不分裡外，這種比喻只是便於大家理解。

克萊因瓶無法被製造的原因

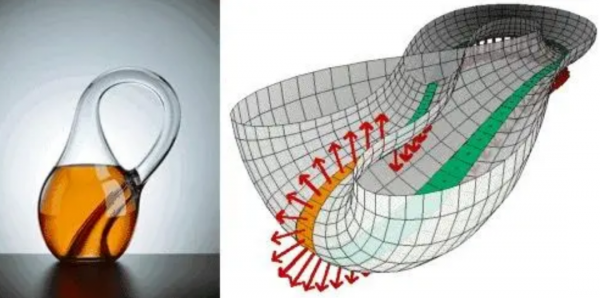
目前市面上一些商家出售的克萊因瓶，都能明顯地看到瓶頸伸入了瓶壁才到達底部。因此按照克萊因瓶的定義來說，這些都是虛假製品，真正的克萊因瓶是無法被製造的，這又是為什麼呢？

先來看看能被製造出的莫比烏斯環的性質，前文提到了它屬於非三維的物體，但是用來製作它的紙條本質上是屬於二維的。大家小時候看的動畫片大部分也是二維的，那上面的人物就像紙片一樣單薄，因此我們也叫它們“紙片人”。所以莫比烏斯環其實是使用二維變換，證明了三維的一些理論。

可是克萊因瓶本質上已經屬於四維空間了，因此我們在三維空間當中製作出的克萊因瓶看起來不倫不類，完全與它的本質不符。克萊因瓶連續性的特質正是導致它無法被製成的根本原因，實際製作當中，這個瓶頸與瓶壁的面勢必會產生相交，導致連續性發生中斷。所以我們看到的商家出售的那些克萊因瓶，早已失去了連續性和單側性，這種瓶子完全不符合克萊因瓶的理論。

所以，三維世界中瓶頸和瓶壁相交的那個點，是它們在三維座標系當中共用了一個位置，如果放進四維空間，就不會有相交的表現。大家可以試著想象將那個位置提起來，繞過瓶壁。就像最初數學家們為了方便我們利用線條理解莫比烏斯環舉的例子，如果在紙上畫一個8，那麼它中間的位置必然是相交的。

但是使用拓撲學，用一個橡皮圈繞著一個8的形狀，那一位置就沒有相交，你可以輕鬆地拿起位於上端的部分。莫比烏斯環從簡單的二維跨越到了三維，正是利用這種方法。

雖然莫比烏斯環本質上也不是三維物體，但是起碼它有一部分是屬於三維的，因此我們能夠按照其定義將模型製作出來。真正的克萊因瓶需要放置在四維空間當中，才能體現出連續性閉合曲面的特質。

具體描述多維度空間很困難

人類的想象力其實已經十分豐富了，我們從來不拘於如今的所見所想，因此我們才一直尋找外星的生命，探尋多維的宇宙。多維是否存在的問題愛因斯坦在一個世紀前的相對論當中就像我們提出了，“物質告訴時空如何彎曲，時空告訴物質如何運動”，在這一理論當中時間和空間是交叉的，並不是傳統意義上的平行線。如果大家有興趣，可以去了解一下廣義相對論當中所描述的彎曲的時空，一定會因此開啟新世界的大門。