導讀：在現實生活中，絕大多數的隨機不是均勻分佈的。
作者：徐晟
來源：華章科技
如果你是一位程式設計師，程式設計時就一定用過隨機（random）函式。它的功能是在特定取值範圍內隨機生成一些數。這個函式在很多程式語言中是預置的，可以直接呼叫。
例如，要從1到100之間隨機生成一個整數，寫程式時就要事先定義一個1到100的取值範圍，然後呼叫隨機函式，得到一個該取值範圍內等機率的隨機數，就是說這100個數中出現任何數字的機率都是1/100。
用慣了隨機函式的程式設計師會誤以為“隨機”就代表了均勻分佈的資料，即等機率事件。這是一個誤區。在現實生活中，絕大多數的隨機不是均勻分佈的。
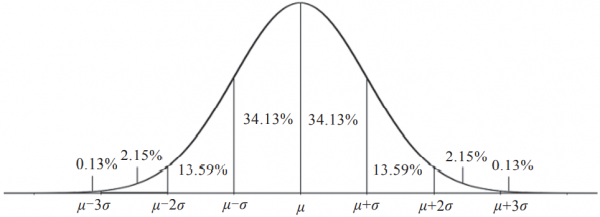
舉個例子，我們知道拋硬幣正反兩面朝上的機率各有一半，但如果你真的拋上10次硬幣，就會發現硬幣正好有5次正面朝上的機率既不是50%，也不是10%，而是在25%左右。因為在自然界中，最普遍的“隨機”是正態分佈（也稱為高斯分佈），其分佈曲線呈“鐘形”，如圖1-1所示。
▲圖1-1 正態分佈數學函式圖
正態分佈是一組資料在正常狀態下的機率分佈。描述這種分佈只需要兩個引數：一是這組資料的平均值，通常用希臘字母μ來表示，它位於函式影象正中間的座標位置。二是標準差，通常用希臘字母σ來表示，它代表了這組資料的離散程度。標準差越小，資料就越集中，反之說明資料越分散。
假如一組資料服從正態分佈，根據分佈特性，其中有68%的數會集中在平均值正負1個標準差區間內，有95%的數會集中在平均值正負2個標準差區間內，有99.7%的數會集中在平均值正負3個標準差區間內。由於3個標準差的區間幾乎涵蓋了大部分資料，因此它在數學中有著非常廣泛的運用，適用於很多場景下的推導和估計。
概括地講，正態分佈說明了“一般的很多，極端的很少”的現象。這種現象生活中很常見。比如，大部分人的身高都在一個區間範圍內，太高或太矮的人不多。仔細觀察身邊的人，可以發現非常聰明或者非常愚笨的人很少。統計全社會範圍內的收入，中檔次收入的人比較多，特別貧窮和特別富裕的人較少。
人們常說的二八法則（也稱帕累托法則），只是換種方式來描述正態分佈現象。二八法則告訴我們，20%的富人擁有世界上80%的財富；只要掌握字典中20%的文字就能理解文章80%的內容；20%的超大城市中居住了80%的人口，等等。
正態分佈的特性還有其他廣泛應用。我們知道，利用多次抽樣可以從相對較少的資料中得出令人信服的總體結論。比如只要調研100個人，就能大致瞭解人類普遍的心理認知。只要抽查100件商品，就能得出這批次商品的質量結論。
這些民意調查、商品抽樣，都在運用抽樣樣本對總體進行估計，其背後的數學原理是中心極限定理。中心極限定理從理論上證明了，無論隨機變數總體呈現什麼分佈，只要抽樣次數足夠大，樣本的平均值將近似服從正態分佈。
也就是說，雖然每個人或者每件商品都會受到大量隨機因素的影響，這些因素會對最終狀態產生一定影響，但我們不必關心這些因素的細節，而只要把人或商品看成一個整體。該整體的統計規律服從正態分佈。
而上述這些情況，才是真實世界中的“隨機”。
關於作者：徐晟，某商業銀行IT技術主管，畢業於上海交通大學，從事IT技術領域工作十餘年，對科技發展、人工智慧有自己獨到的見解，專注於智慧運維（AIOps）、資料視覺化、容量管理等方面工作。
本文摘編自《大話機器智慧：一書看透AI的底層執行邏輯》，經出版方授權釋出。（ISBN：9787111696193）
《大話機器智慧：一書看透AI的底層執行邏輯》
推薦語：AI是什麼？機器如何擁有“智慧”？“智慧”如何起作用？本書以通俗易懂的方式，勾勒人工智慧的全貌，展現AI的底層執行邏輯，即AI是如何工作的。
