世界上許多古代偉大建築,隨著歲月的流逝,有的倒塌了,有的消失了,只有金字塔巋然傲立。這其中有什麼秘密呢?我們先來做個試驗。
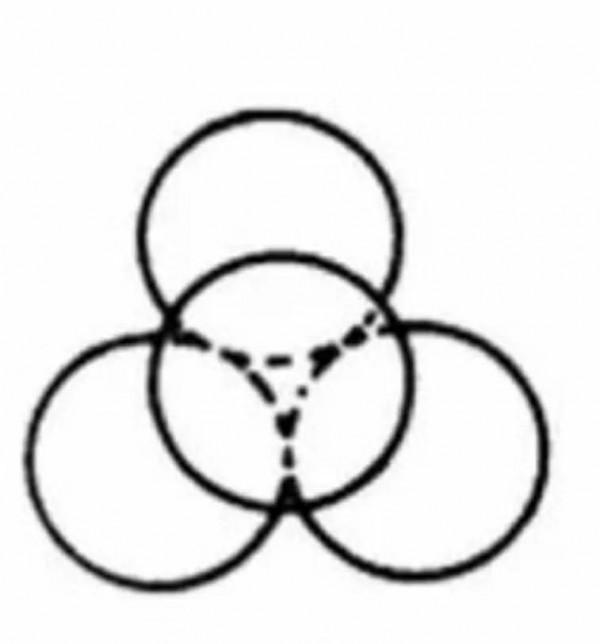
把一些米、沙子、碎石子分別自上而下慢慢傾倒,我們發現,一會兒它們就形成了3個圓錐。儘管質量、體積不同,但形成的形狀卻異常相似。它們的錐角角度相同,都是52度。
52度,這種自然形成的角是最穩定的角,人們把它稱為“自然塌落現象的極限角和穩定角”。
金字塔的錐角正好是51度50分9秒,說明金字塔就是按照這種“極限角和穩定角”來建造的。胡夫金字塔是最大的金字塔,也是法國埃菲爾鐵塔建成前世界上最高的建築物,經歷了3次地震,至今依然屹立不倒。
為什麼自然界中物體自然堆積的極限角和穩定角為52° ?
這個問題被一位名叫 “郭敦顒(yóng)”的人給完美解決了。他的解決方法2010年12月3號發表在百度百科上。
我今天只是重新敘述一下他的方法,做一回知識的搬運工。
解決過程如下:
無論是米、沙子或碎石子,它們堆積在一起,從微觀上說,(以石子為例)每一粒石子下面都有三顆石子,上面的那顆石子位於下面三顆石子的中央,只有這樣才能保持穩定。
那接下來我們就計算一下堆積在一起的呈正四面體的四個球(下面三個球呈三角形排列,上面中心處放一個球)所形成的角度。
(如上面三幅圖)
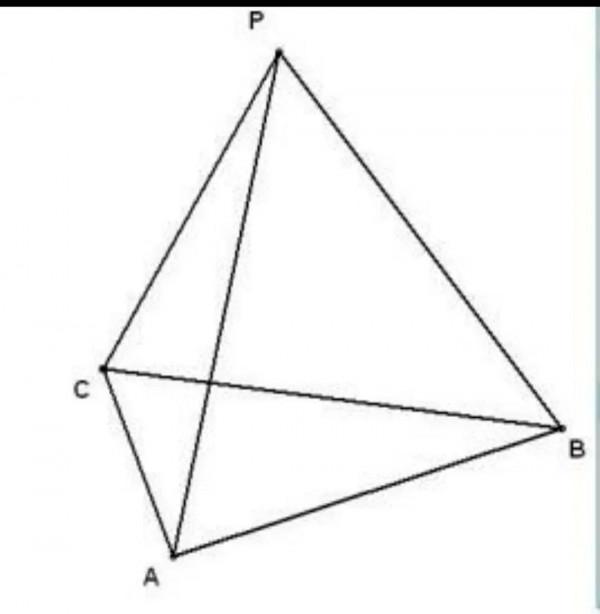
然後我畫了兩幅圖,具體分析,圖如下:
這是墊在下面的三個球,分別命名為球A(球心為A)、球B(球心為B)、球C(球心為C)。
三個球的球心分別為A、B、C,三個球兩兩相切,球的半徑都是1cm。
則AB= 2cm , BC=2cm , AC=2cm ,三角形ABC是等邊三角形。
過C點作CF⊥AB , 過A點作AD⊥BC , 過B點作BE⊥AC,三條線交於G點。則G點是三角形ABC的重心。
在下面這三個球上面還有一個球P(球心是P)。
球P與下面三個球分別相切。
連線PG,則PG垂直於三角形ABC所在的平面,當然PG也垂直於AG。
由於三角形ABC是等邊三角形,它的三個內角都是60º,AD⊥BC,易得AD平分 ∠CAB,所以
∠DAB=30º
直角 △DAB中,∠DAB=30º,AB=2cm,BD=1cm,可以求出 AD=√3cm 。
在直角△GDB中,∠DBG=30º,可以得到∠DGB=60º ,在這個內角分別是30º、60º、90º的直角三角形中,三條邊長度的比是
1:√3:2 。
所以 DG/DB = 1/√3 ,由於DB=1cm,所以可以求出DG=1/√3 cm 。
在直角△ADB中,∠DAB=30º,∠DBA=60º ,在這個內角分別是30º、60º、90º的直角三角形中,三條邊長度的比是 1:√3:2 。由於AB=2cm, BD=1cm,可以得到AD=√3cm。
所以:AG=AD-DG
= √3cm- 1/√3 cm
=(2/3)· √3 cm
P是上面一個球的球心,球P與球A相切,所以PA=2cm ,又PG⊥AG,所以△PGA是直角三角形。在直角△PGA中,∠PGA=90º,PA=2cm,
AG =(2/3)· √3 cm ,
所以cos∠PAG = AG/PA(即求∠PAG的餘切)
=(2/3)· √3 cm ÷ 2cm
= 0.57736666
所以∠PAG = 54.73°
54.73°就是自然界中物體自然堆積的極限角和穩定角。
為什麼自然界中物體自然堆積的極限角和穩定角是52° ?因為在自然界中,物體自然堆積形成立體結構時不可能毫無間隙地緊挨在一起,不可能構成完美的正四面體,總是有一定的鬆散度,所以自然界中物體自然堆積的極限角和穩定角大約是52º 。
這就是自然塌落現象的極限角與穩定角約是52度的數學證明。