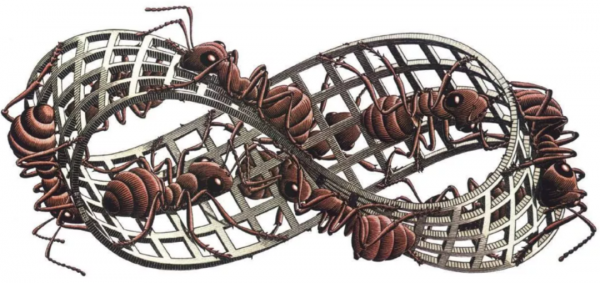
科學家們根據近現代科學知識體系,總結出了11個維度空間,第一維到第三維是存在於空間範圍裡的位置,比如長、寬、高,而此後則是科學家們的猜想,只是人類還沒有實際的證據來證明它們的存在,對這些三維以上的空間也並沒有一個準確的認識。
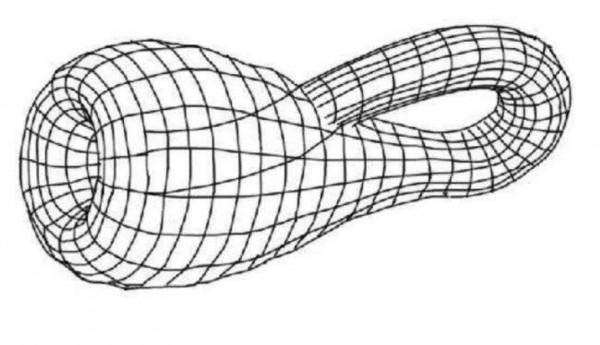
很多人直到現在也沒有明白其他的多維空間是什麼,而科學家們也在不斷地對多維空間的存在進行研究和“試探”,比如德國的數學家菲利克斯·克萊因在1882年發現並命名的“克萊因瓶”,這是一個哪怕將地球上的所有水倒入都無法裝滿的神奇瓶子。今天我們就來了解一下這個著名的“克萊因瓶”。
克萊因瓶是什麼
菲利克斯·克萊因出生於1849年4月25日,他大學學習的是數學和物理,原本他有著一個成為物理學家的夢想,卻因為教授菲利克斯·克萊因知識的教授忽然去世,菲利克斯·克萊因為了完成教授沒有做完的幾何課題,走向了數學家的道路。
1882年,菲利克斯·克萊因提出了“Kleinsche Fläche”,這在德語裡是意思是“克萊因平面”,然而因為翻譯有誤,後面的“平面”成為了“Flasche”,也就是“瓶子”的意思,即“克萊因瓶”。
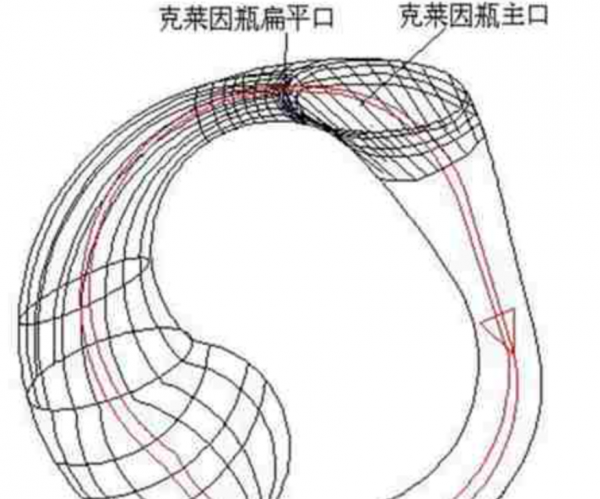
雖然看起來是翻譯錯誤了,但其實“瓶子”與菲利克斯·克萊因所描述的平面形象還是非常貼切的。這個“克萊因瓶”的結構大概是這樣的:一個底部存在一個洞的瓶子,再將瓶子的瓶頸拉長,延伸進入瓶內與瓶底的洞相連。這樣聽起來是不是很簡單?實際上這是一個沒有“邊”,如同球面一樣表面無邊無際,永不終結的單個曲面。
同時克萊因瓶也不存在內外的區別,內外是相通的,一隻蚊子能夠從“克萊因瓶”的內部直接飛出去,而不需要跨越瓶壁,或者說,克萊因瓶根本就沒有瓶內和瓶壁之說,是一個有外而無內的神奇東西。
從數學學科的角度來看,克萊因瓶並不是一個真實的瓶子,而只是一種平面,它只是在我們的眼裡看起來像是一個瓶子的外形,而且還是瓶頸穿進瓶身,再與瓶底的洞連線的物體。
然而實際上,克萊因瓶並未發生相交的行為,只是克萊因瓶的瓶頸與瓶身上的某些點處在了三維空間的相同位置,這才導致了在三維空間的我們看來,它們是相交的狀態。
應該說克萊因瓶是一個只能存在於四維空間裡的曲面,它的瓶頸是在四維空間裡與瓶底相連,根本不需要從瓶身上面穿過去。
也因此,之所以地球上的水都無法將克萊因瓶裝滿,不是因為什麼神乎其神的“黑洞效應”等等,而是因為克萊因瓶本身只是一個平面,它沒有圈住空間,也沒有內外之分,倒入克萊因瓶的水也會立刻流出去,自然也就無法“裝滿”了。
而有一些人拿著市面上所謂的“克萊因瓶”裝上水,然後以此來反駁“克萊因瓶無法裝滿水”的觀點,這是極其錯誤且無知的行為。
因為我們之前也有說過,這是一個只能存在於四維空間的平面,在我們所在的三維空間裡,無論是科學家也好,還是什麼大師級別的能工巧匠都無法將真正的克萊因瓶製作出來。
畢竟在三維空間裡,想要實現菲利克斯·克萊因所說的克萊因瓶的構成,必須要將瓶身與瓶頸相交。那些所謂的“克萊因瓶”也只是人們憑著克萊因瓶在三維空間裡所展現的冰山一角所製作的,它無法代表真正的克萊因瓶。
莫比烏斯環
如果還是無法理解克萊因瓶是什麼,那我們可以將克萊因瓶沿著對稱線分割,就能得到2個對稱的“莫比烏斯帶”。
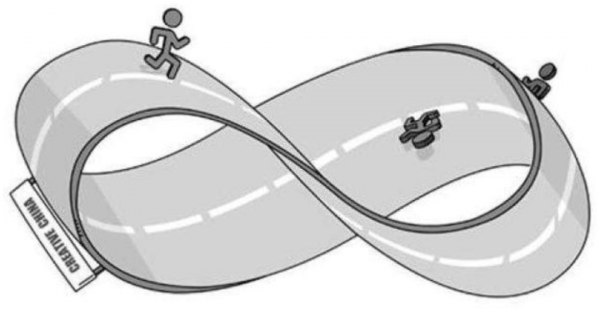
這是莫比烏斯和另外一位科學家在1858年發現的現象,製作方式很簡單,並且不像是克萊因瓶無法在三維世界裡製造出來,莫比烏斯環只需要準備一個紙帶,並將其中一端固定住,另外一端扭轉180度,或者是任意的180的奇數倍度數,再將兩端連線。
這個莫比烏斯帶只有一個曲面,而不像是普通的一個紙帶一樣具有正反兩面,將一隻螞蟻放在莫比烏斯帶中,它甚至可以不用跨越莫比烏斯帶的邊界,或者說是不用自行翻個面,就能走遍整個曲面。
莫比烏斯帶是兩個面的連線,本質上只有一個面,也就無法定義到底什麼地方是裡面,什麼地方是外面,是“二維空間中一維可無限擴充套件之空間模型”。
克萊因瓶與莫比烏斯帶有著異曲同工之處,它是一個平面進行翻轉、扭曲後,將多個面進行合一的結果,因此才會說它只有一個面。
如果我們在四維空間裡,我們就能夠將兩條莫比烏斯環組成一個克萊因瓶,其實除了這個瓶子的形狀,克萊因瓶還有另外一個很少有人知道的三維世界的形狀——“8字形”,雖然兩個形狀在我們的眼裡有著巨大的差別,但在四維空間裡,它們其實就是一個平面罷了。
為什麼克萊因瓶在三維世界是相交的?
當然,可能還會有人很疑惑,為什麼克萊因瓶在四維空間是一個不相交的曲面,卻在三維空間就相交了呢?我們從四維空間的角度可能很難更加詳細精準地解釋,那就換一個維度空間來分析一下。我們都知道,一維空間是一個點,它只有一個單位,比如往前或者往後,任何一個平面或者是空間在一維空間裡都只能表現為一個點的形狀。
二維空間則是平面,即只有前後、左右,而無法進行上下的活動,三維空間也就是我們所在的世界,具有長、寬、高三種位置方向,不僅能夠進行前後、左右的活動,還能上下移動。
在三維空間裡,我們把一個圈扭轉卻不相交,在我們的眼裡它只是形狀有所變化,根本沒有發生碰觸,但是在二維空間裡,這卻是一個具有交點的圈。
再比如我們將兩根筷子一個朝下,一個朝前放置,它們本身是平行且不相交的,但是二維世界的人也只會看到交叉的兩根筷子。
這就是從低緯度觀察高緯度的缺點,低緯度的人總會缺少一些它們所無法理解的東西,因此只能發現它們能夠發現的事情。就算是我們告訴一個生活在二維空間的人:一個蘋果是由多個平面組成的,一個長方體有六個面等等,它們也都無法理解這是什麼意思。
換句話說,我們的維度相對克萊因瓶比較低,在我們的認知裡世界只有長、寬、高,所以無法理解克萊因瓶到底是怎麼組成的。而克萊因瓶的這個形象也不過是它在三維空間的一個“投影”,是我們只能夠看見和理解的部分。
四維空間是什麼
那麼四維空間到底是什麼呢?其實科學家們還沒有一個對四維空間準確的結論,目前而言也只是一個基於現有科技手段和理論知識上進行的對規律的猜想。
這裡說的四維空間與愛因斯坦的“四維時空”並不一樣,後者指的是宇宙是在三維空間的“空間”基礎上,再與另外一個維度——“時間”共同組成的,其中的“第四維”與三個維度有著很大的差異:一個是時間,三個是空間。
而我們所說的四維空間,“第四維”與三種維度都屬於是空間,從數學的角度來說,第四維就是在x軸、y軸、z軸的基礎上,再延伸出來的一條同時垂直於這三條座標軸的軸線,一般來說是將這條軸線稱為是“w軸”。
這也就意味著,四維空間除了前後、左右、上下的三種活動方向以外,還存在著另外一種新的移動方向,這是三維空間的我們所無法做到的。
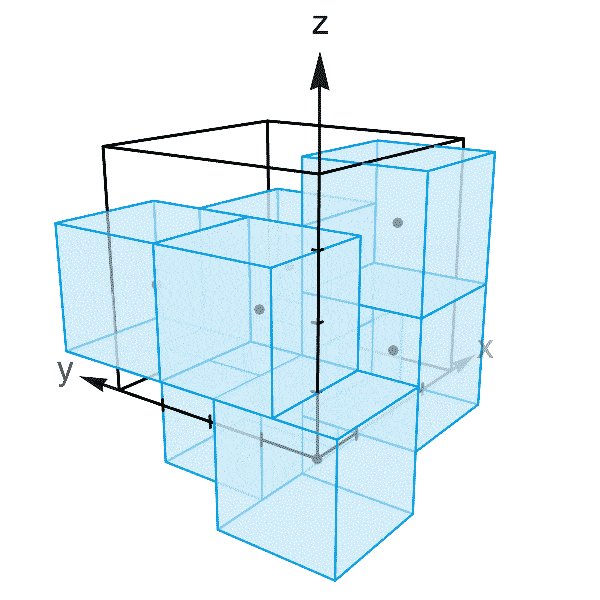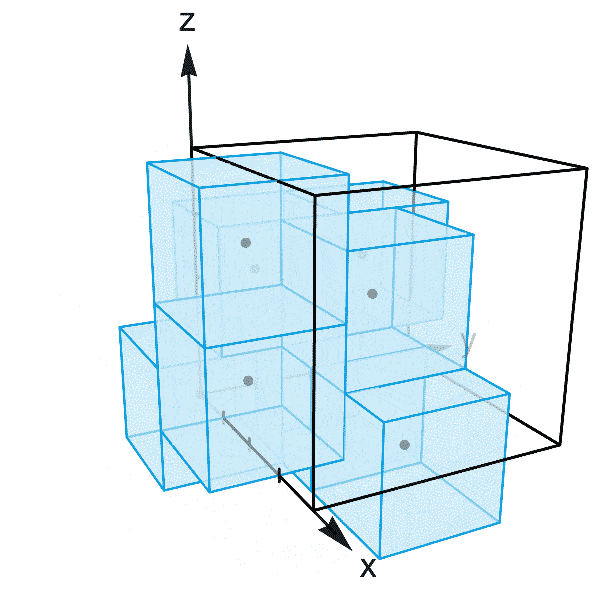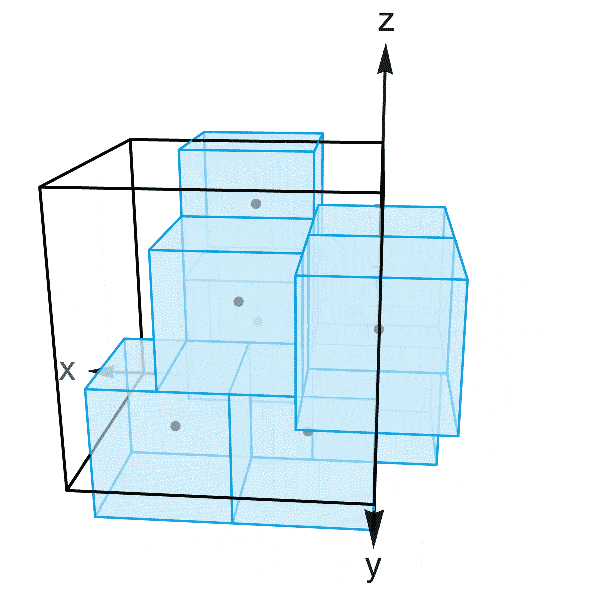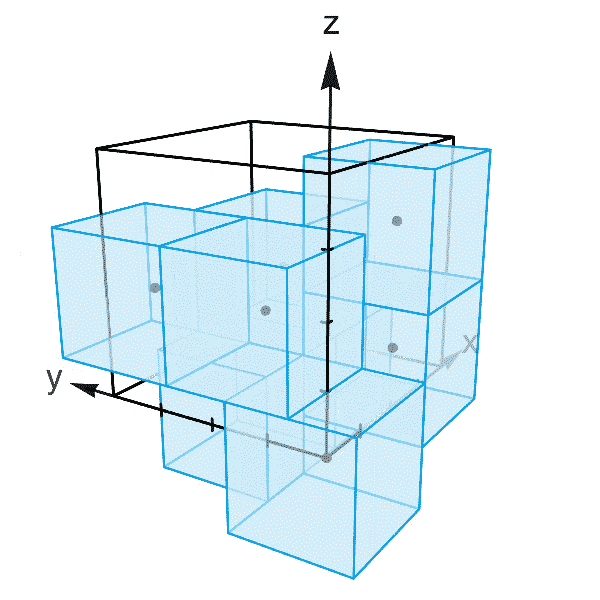
二維空間(平面)是由多個一維空間(點)組成的,三維空間是由多個二維空間組成的,按照這樣的規律來看,那麼四維空間也應該是由多個三維空間構成的,是多個平行的三維空間的堆積。
一本叫做《扁平世界》的書裡描繪了一群生活在二維空間的人,對於他們來說,三維空間的人類就像是神仙一樣——三維空間的人能夠看見在二維空間裡的人認為被遮擋在牆後的物體,也能夠在不破壞掉二維空間的保險箱的前提下輕鬆地將裡面的物體取出來。
甚至只要三維空間的人朝著平面以外的位置移動一點距離,對於二維空間的人來說就如同隱身了一般,永遠也無法再找到他的蹤跡。
同理,對於我們而言,超出了三維空間的生物也必然是具有“神力”的神仙,哪怕是我們的保險櫃,它們也能夠從另外的一個維度將內部的物體取走,也同樣能在我們面前“隱身”。
事實上,我們也不必為此感到驚慌和擔憂,多維空間還只是科學家們的推測而已,事實到底是什麼樣子的,面前還沒有人能夠知道。