如何在大海撈針中找到一根針？在第二次世界大戰之交，當醫生想知道如何有效地檢測被徵召參加戰爭的人的疾病時，這個問題呈現出非常具體的形式。受到這一挑戰的啟發，當時年輕的統計學家羅伯特·多夫曼（後來成為哈佛大學經濟學教授）在一篇開創性的論文中提出一種檢測受感​染個體的兩階段方法，即在測試是否存在病原體之前，首先將個體血液樣本分成四組。如果一個組為陰性，則可以安全地假設該組中的每個人都沒有病原體。在這種情況下，所需測試數量的減少是顯著的：整個四人組透過一次測試就可以透過。另一方面，如果一組檢測呈陽性（如果病原體的流行率很小，預計這種情況很少發生），則該組中至少有一個或多個人必須呈陽性；因此，需要進行更多的測試來確定受感染的個體。

多爾夫曼的建議引發很多後續工程與計算機科學的幾個領域，如連線資訊理論，組合學或壓縮感知，以及他的做法幾個變種已經被提出，尤其是那些利用二元分割或側知識個體 感染機率率. 該領域已經發展到幾個子問題被認可並值得單獨閱讀整個文獻的程度。一些演算法是為測試完全可靠的無噪聲情況量身定製的，而另一些演算法則考慮測試有噪聲的更現實的情況並且可能產生假陰性或陽性。最後，一些策略是自適應的，根據已經觀察到的測試結果提出組（包括 Dorfman，因為它建議重新測試出現在陽性組中的個體），而其他策略則堅持非自適應設定，其中預先知道組或隨機抽取。

在“使用貝葉斯序列實驗設計的噪聲自適應組測試”，我們提出了一種組測試方法，該方法可以在嘈雜的環境中執行（即測試可能出錯的地方），透過檢視過去的結果來自適應地決定接下來要測試的組，目標是儘快收斂到可靠的檢測，並儘可能少地進行測試。大規模模擬表明，這種方法可能會顯著改善適應性和非適應性基線，並且在疾病流行率較低時比單獨測試更有效。因此，這種方法特別適合需要在有限資源下進行大量測試的情況，例如與 COVID-19 傳播相對應的大流行病。我們已透過GitHub 儲存庫將程式碼開源給社群。

非漸近機制中的嘈雜和自適應組測試

組測試策略是一種演算法，其任務是猜測在n個人的列表中誰攜帶特定病原體。為此，該策略提供了將個人分組的說明。假設一個實驗室一次可以執行k 個測試，該策略將形成一個k ⨉ n池化矩陣來定義這些組。一旦進行測試，結果將用於決定是否收集了足夠的資訊來確定誰被感染或未被感染，如果沒有，如何組成新的組進行另一輪測試。

我們為現實環境設計了一種組測試方法，其中測試策略可以是自適應的，而測試是嘈雜的——受感染樣本的測試呈陽性的機率（靈敏度）小於 100%，特異性、機率也小於 100%。未感染的樣本返回陰性。

使用貝葉斯最佳化實驗設計以更少的測試篩選更多的人

我們提出的策略以偵探調查案件的方式進行。他們首先使用迄今為止進行的所有測試（如果有）的證據以及有關感染率的先前資訊（a），形成關於誰可能被感染或可能未被感染的幾個假設。使用這些假設，我們的偵探產生一個可操作的專案來繼續調查，即下一波可能有助於驗證或使盡可能多的假設無效的小組 (b)，然後迴圈回到 (a)，直到一組合理的假設小到足以明確識別搜尋目標。更確切地說，

a. 給定n人的人口，感染狀態是一個長度為n的二進位制向量，它描述了誰被感染（用 1 標記），誰沒有被感染（用 0 標記）。在某個時間，種群處於給定狀態（很可能是幾個 1，大部分是 0）。組測試的目標是使用盡可能少的測試來識別該狀態。鑑於對感染率（這種疾病很少見）和迄今為止觀察到的測試結果（如果有的話）的先驗信念，我們預計這些感染狀態中只有一小部分是合理的。我們沒有評估所有2 n 個可能狀態（即使對於很小的n也是非常大的數字）的合理性，而是採用更有效的方法來取樣使用順序蒙特卡羅(SMC)取樣器的合理假設。儘管按照通用標準（在我們的實驗設定中使用 GPU 需要幾分鐘）相當昂貴，但我們在這項工作中表明，即使對於大n SMC 取樣器仍然易於處理，為組測試開闢了新的可能性。簡而言之，作為幾分鐘計算的回報，我們的偵探會得到數千個相關假設的廣泛列表，這些假設可以解釋迄今為止觀察到的測試。

b.配備了相關的假設列表，我們的策略會像偵探一樣透過有選擇地收集額外證據來進行。如果在下一次迭代中可以進行k 個測試，我們的策略將建議測試k 個新組，這些組是使用貝葉斯最優實驗設計的框架計算的。直觀地說，如果k=1並且一個人只能提出一個新組進行測試，那麼構建該組使其測試結果儘可能不確定，即返回正值的機率儘可能接近鑑於當前的一組假設，儘可能為 50%。事實上，要在調查中取得進展，最好將意外因素（或資訊增益）由新的測試結果提供，而不是使用它們來進一步確認我們已經認為很有可能的情況。為了將這個想法推廣到一組k>1 個新組，我們透過計算這些“虛擬”組測試的互資訊與假設分佈來對這個驚喜因素進行評分。我們還考慮了一種更復雜的方法，該方法計算ROC 曲線下的預期面積(AUC)，該方法可以使用假設分佈從測試這些新組中獲得。這兩個標準的最大化是使用貪婪的方法進行的，導致兩個組選擇器、GMIMAX 和 GAUCMAX（互資訊或 AUC 的貪婪最大化）。

wet_lab進行測試 的實驗室 ( ) 與我們的策略（由 asampler和 a組成）之間的互動group selector在下圖中進行了總結，該圖中使用了在我們的開源包中實現的類的名稱。

基準

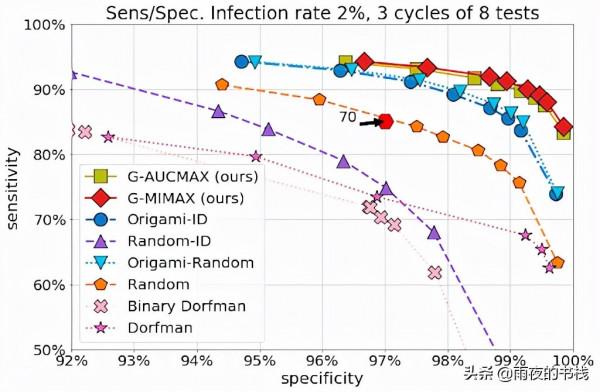
測試 我們針對各種設定（感染率、測試噪聲水平）中的各種基線對我們的兩種策略 GMIMAX 和 GAUCMAX 進行了基準測試，隨著測試數量的增加報告效能。除了簡單的 Dorfman 策略之外，我們考慮的基線還包括非自適應策略（摺紙分析、隨機設計）的混合，並在後期與所謂的資訊性 Dorfman 方法相輔相成。我們的方法在所有設定中都明顯優於其他方法。

結論

篩查人群中的病原體是一個基本問題，這是我們目前在當前 COVID-19 流行期間面臨的問題。七十年前，多夫曼提出了一種目前被各個機構採用的簡單方法. 在這裡，我們提出了一種以多種方式擴充套件基本組測試方法的方法。我們的第一個貢獻是採用機率觀點，並根據測試結果形成數以千計的感染分佈假設，而不是像 Dorfman 那樣相信測試結果是 100% 可靠的。這種觀點使我們能夠無縫地結合有關感染的其他先驗知識，例如，當我們懷疑某些人比其他人更可能攜帶病原體時，例如基於接觸者追蹤資料或對問卷的回答。這提供了我們的演算法，可以將其與調查案件的偵探進行比較，瞭解最有可能的感染假設是什麼，這些假設與迄今為止進行的先前信念和測試一致。