當前人工智慧領域的先進技術層出不窮,諸如計算機視覺、自然語言處理、影像生成,深度神經網路等先進技術日新月異。然而,從計算能力、記憶體或能源消耗角度來看,這些新技術的成本可能令人望而卻步,其中某些成本對於大多數硬體資源受限的使用者來說,則完全負擔不起。所以說,人工智慧許多領域將對神經網路進行必要的修剪,在確保其效能的同時降低其執行成本。
這就是神經網路壓縮的全部要點,在這一領域,有多種方法來實現神經網路的壓縮,如量化、分解蒸餾等等,本文的重點在於闡述神經網路的剪枝。
神經網路剪枝旨在去除效能良好但花費大量資源的多餘部分網路。儘管大型神經網路的學習能力有目共睹,但事實上,在訓練過程結束後,並不是所有的神經網路全部有用,神經網路剪枝的想法便是在不影響網路效能的情況下去除這些無用的部分。
在這個研究領域,每年均有幾十篇,甚至數百篇論文釋出,眾多的論文揭示了這一想法蘊含的複雜性。透過閱讀這些文獻,可以快速識別出神經網路的無用部分,並在訓練前後去除它們,值得強調的是,並不是所有的修剪都可以提速神經網路,某些工作甚至會事倍功半。
本文在閱讀原生神經剪枝論文的基礎上,提出瞭解決神經網路修剪的解決方案,依次回答了三個這一領域中的核心問題:“應該對哪部分進行修剪?”、“如何判斷哪些部分可以修剪?”以及“如何在不損害網路的情況下進行修剪?”。綜上所述,本文將詳細介紹神經網路剪枝的結構、剪枝準則和剪枝方法。
1 —剪枝的結構
1.1 — 非結構化剪枝
當涉及神經網路的成本時,引數的數目和FLOPS(每秒鐘的浮點操作次數)是其中最廣泛使用的指標之一。看到網路顯示出天文數字的引數(對某些人來說會花費高達數十億美元的成本),這的確令人生畏。透過直接刪除引數,從而直觀地減少引數數目,這一方法肯定有效。實際上,這一方法在多個文獻中均有提及,修剪引數是文獻中提到的應用最為廣泛的示例,被視為處理剪枝時的預設框架。
直接修剪引數的方法有諸多優點。首先,它很簡單,在引數張量內,將其權重值設為零,便可以實現對引數的修剪。在Pytorch深度學習框架中,可以輕鬆地訪問到網路的所有引數,實現起來非常簡單。儘管如此,修剪引數的最大優勢是:它們是網路中最小、最基本的元素,因此,只要數量足夠多,便可以在不影響效能的情況下,對它們進行大量修剪。這種精細修剪的粒度使得可以在非常精密的模式下實現剪枝,例如,可以對卷積核心內的引數進行修剪。由於剪枝權值根本不受任何約束條件的限制,而且是修剪網路的最好方法,因此將這種方式稱為非結構化剪枝。
然而,這種方法的致命缺點是:大多數深度學習框架和硬體無法加速稀疏矩陣的計算,這意味著無論你為引數張量填充多少個零,都不會對實際訓練成本產生實質的影響,僅僅是一種直接改變網路架構的方式進行剪枝,而不是對任何框架都放之四海而皆準的方法。
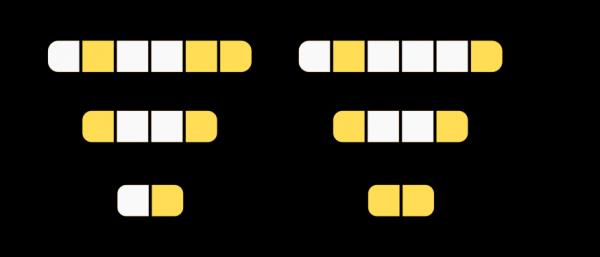
非結構化(左)和結構化(右)剪枝之間的區別:結構化剪枝會同時刪除卷積過濾器和核心行,而不僅僅是修剪引數。從而使得中間特徵對映的數目更少。
1.2 —結構化剪枝
結構化剪枝專注於對更為龐大的結構進行修剪,比如修剪整個神經元,或者,在更現代的深度卷積網路中,直接修剪卷積過濾器。大型網路往往包含許多卷積層,每個層中包含數百或數千個過濾器,可以對卷積層過濾器進行細粒度的修剪。移除這種結構不僅使得深度神經網路的層結構更為稀疏,而且這樣做還可以去除過濾器輸出的特性對映。
由於減少了引數,這種網路不僅儲存起來更為輕便,而且計算量也得以降低,生成更為便捷的中間表示,因此在執行時需要更少的記憶體。實際上,有時降低頻寬比減少引數數目更有益。對於涉及大型影象的任務,如語義分割或物件檢測,中間表示可能比網路本身更加消耗記憶體,出於這些原因,可以將過濾器修剪視為預設的結構化剪枝。
在應用結構化剪枝時,應注意以下幾方面:首先,應考慮如何構建卷積層,對於Cin輸入通道和Cout輸出通道,卷積層由Cout過濾器構成,過濾器分別對Cin核心進行計算;每個過濾器均輸出一個特徵對映,每個輸入通道為一個核心專用。基於這種架構,卷積網路為堆疊的多個卷積層,當對整個過濾器進行剪枝時,可以觀察到對每一個過濾器剪枝的過程,隨後輸出特徵對映,這一過程也會導致對後續層核心的修剪。這意味著,當修剪過濾器時,在第一次刪除引數之後,實際刪除的引數數量是最初認為要刪除的引數數量的數倍。
下面來考慮一下這種特殊情況,當一不留神把所有卷積層都修剪掉之後(雖然卷積層被修剪掉了,但神經網路並沒有被摧毀,這由神經網路的架構來決定),無法連結到前一層的輸出,這也可以是神經網路的一種剪枝方式:修剪掉所有卷積層,實際上等於修剪掉了所有上一層的輸出,所以只能連線到其他地方(如殘餘連線或並行通道)。
在對過濾器剪枝時,首先應該計算出實際引數的確切數量,再根據過濾器在神經網路架構中的分佈,修剪相同數量的過濾器,如果實際引數的數量與修剪引數數量不同,結果將不具備可比性。
在進入下一個主題之前,需要提及的是:依然有少數工作集中於剪枝卷積核心、核內架構乃至是特定的引數結構。然而,這些架構需要用特殊的方法來實現(如非結構化剪枝)。此外,另一種方法是對每個核中的某個引數進行修剪,將卷積層轉換為“移位層”,這可以透過一次移位操作和一次1×1卷積的組合來實現。
結構化剪枝的缺點:輸入和輸出維度的改變會引發某些偏差。
2 —剪枝原則
在決定了採用何種結構進行剪枝之後,下一個問題便會是:“現在,如何找出保留哪些部分,哪些部分需要修剪?”為了回答這個問題,透過對引數、過濾器或其他特性進行排序基礎上,生成一個恰當的剪枝準則。
2.1 —權重大小準則
一個非常直觀而又有效的準則是:修剪掉那些權重絕對值最小的引數。事實上,在權重衰減的約束條件下,那些對函式沒有顯著貢獻的引數在訓練期間,它們的幅度會不斷減小。因此,那些權重比較小的引數便顯得多餘了。原理很簡單,這一準則在當前神經網路的訓練中被廣泛使用,已成為該領域的主角。
儘管這個準則在非結構化剪枝的實現中顯得微不足道,但大家更想知道如何將其應用於結構化剪枝。一種簡單的方法是根據過濾器的範數(例如L1或L2)對過濾器進行排序。這種方法實現起來簡單粗暴,即將多個引數封裝在一起:例如,將卷積過濾器的偏差和批歸一化引數封裝到一起,將在並行層的過濾器輸出融合起來,從而減少通道數目。
其中一種方法是:在無需計算所有引數的組合範數的前提下,為需要修剪的每一層的特徵對映插入一個可學習的乘法因子,當它減少為零時,有效地刪除負責這個通道的所有引數集,該方法可用於修剪權重幅度較小的引數。
2.2 —梯度大小剪枝準則
權重大小剪枝準則並非唯一流行的準則,實際上,還有另一個重要準則,即梯度大小剪枝準則,也非常適用。根據上世紀80年代的一些基礎理論,透過泰勒分解去消除引數對損失的影響,某些指標:如反向傳播的梯度,可提供一個不錯的判斷方法,來確定在不損害網路的情況下可以修剪掉哪些引數。
在實際專案中,這一準則是這樣實現的:首先計算出小批次訓練資料的累積梯度,再根據這個梯度和每個引數對應權重之間的乘積進行修剪。
2.3 —全域性或區域性剪枝
最後一個需要考慮的因素是,所選擇的剪枝準則是否適用於網路的所有引數或過濾器,還是為每一層獨立計算而設計。雖然神經網路全域性剪枝可以生成更優的結果,但它會導致層垮塌。避免這個問題的簡單方法是,當所使用的全域性剪枝方法無法防止層垮塌時,就採用逐層的區域性剪枝。
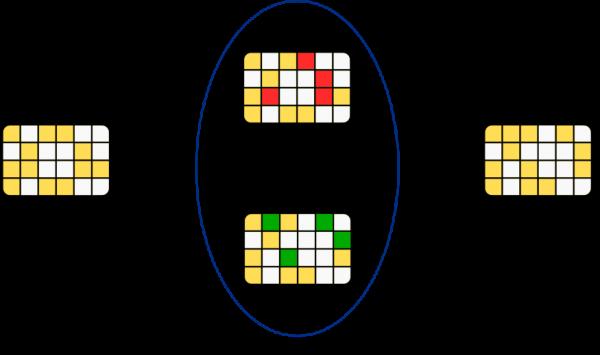
區域性剪枝(左)和全域性剪枝(右)的區別:區域性剪枝對每一層分別進行剪枝,而全域性剪枝同時將其應用於整個網路
3 —剪枝方法
在明確了剪枝結構和剪枝準則之後,剩下就是應該使用哪種方法來剪枝一個神經網路。這實際上是最令人困惑的話題,因為每一篇論文都會帶來自己的獨有的剪枝方法,以至於大家可能會對到底選用什麼方法來實現神經網路的剪枝感到迷盲。
在這裡,將以此為主題,對目前較為流行的神經網路剪枝方法作一個概述,著重強調訓練過程中神經網路稀疏性的演變過程。
3.1 — 經典的框架:訓練、剪枝和微調
訓練神經網路的基本框架是:訓練、剪枝和微調,涉及1)訓練網路2)按照剪枝結構和剪枝準則的要求,將需要修剪的引數設定為0(這些引數之後也無法恢復),3)新增附加的epochs訓練網路,將學習率設為最低,使得神經網路有一個從剪枝引起的效能損失中恢復的機會。通常,最後兩步可以迭代,每次迭代均加大修剪率。
具體剪枝方法如下:按照權重大小剪枝原則,在剪枝和微調之間進行5次迭代。實驗表明,透過迭代可以明顯提高訓練效能,但代價是要花費額外的算力和訓練時間。這個簡單的框架是許多神經網路剪枝的基礎,可以看作是訓練神經網路的預設方法。
3.2 —經典框架的拓展
有一些方法對上述經典框架做了進一步的修改,在整個訓練過程中,由於刪除的權重越來越多,加速了迭代過程,從而從迭代的優勢中獲益,與此同時,刪除整個微調過程。在各個epoch中,逐漸將可修剪的過濾器數目減少為0,不阻止神經網路繼續學習和更新,以便讓它們的權重在修剪後能重新增長,同時在訓練中增強稀疏性。
最後,Renda等人的方法指出:在網路被修剪後進行重新再訓練。與以最低學習率進行的微調不同,再訓練採用與原先相同的學習率,因此稱這種剪枝方法為“學習率重繞”。這種剪枝後再一次重新訓練的方法,比微調網路的效能更優。
3.3 —初始化時剪枝
為了加快訓練速度,避免微調,防止訓練期間或訓練後神經網路架構的任何改變,許多工作都集中在訓練前的修剪上:斯摩稜斯基在網路初始化時便對網路進行修剪;OBD(Optimal Brain Damage)在對網路初始化剪枝時採用了多種近似,包括一個“極值”近似,即“假設在訓練收斂後將執行引數刪除”,這種方法並不多見;還有一些研究對這種方法生成掩碼的能力提出了保留意見,神經網路隨機生成的每一層的掩碼具有相似的分佈特性。
另一組研究剪枝和初始化之間關係的方法圍繞著“彩票假說”展開。這一假設指出,“隨機初始化的密集神經網路包含一個初始化的子網,當隔離訓練時,它可以在訓練相同次數迭代後匹配原始網路的測試精度”。專案實踐中,在剛剛初始化時,便使用已經收斂的剪枝掩碼。然而,對這一剪枝方法的有效性,還存在著諸多質疑,有些專家認為,利用特定掩碼來訓練模型的效能甚至可以優於用“勝券”假設下獲得的效能。
經典的剪枝框架、彩票假說的學習率調整比較
3.4 —稀疏訓練
上述方法均共享相同的底層主題:在稀疏性約束下的訓練。這一原則以一系列稀疏訓練方法為核心,它包括在訓練分佈變化的情況下,執行恆定的稀疏率並逐步調整。由Mocanu等人提出,它包括:
1)用一個隨機掩碼初始化網路,並對網路進行一定比例的修剪
2)在一個epoch內訓練這個修剪過的網路
3)修剪一定數量較小的權值,4)再生相同數量的隨機權值。
這種情況下,剪枝掩碼是隨機的,被逐步調整以瞄準最小的匯入權值,同時在整個訓練過程中強制執行稀疏性。各層或全域性的稀疏性級別可以相同。
稀疏訓練在訓練過程中週期性期切割和增長不同的權重,經過調整後的權重與相關引數的掩碼相關
3.5 —掩碼學習
還有一些方法側重於在訓練期間學習掩碼修剪,而不是利用特定準則來修剪權重。在這一領域,比較流行的有以下兩種方法:1)對網路或層分開進行掩碼學習,2)透過輔助引數進行掩碼學習。第一種方法中可以採用多種策略:儘可能多的修剪的每層的過濾器,在最大限度地提高精度的前提下,插入基於attention的層或使用強化學習。第二種方法將剪枝視為一個最佳化問題,它傾向於最小化網路的L0範數和監督損失。
由於L0是不可微的,有些方法主要圍繞著使用輔助的懲罰引數來實現,在前向通路中,將輔助的懲罰引數乘以其相應的引數來規避這個問題。還有一些方法採用了一種類似於“二進位制連線”的方法,即:在引數選擇時,應用隨機門的伯努利分佈,這些引數p利用“直接估計器”或其他學習方法獲取。
3.6 —基於懲罰的方法
有許多方法應用各種懲罰來增加權重,使它們逐步收縮為0,而不是透過手動修剪連線或懲罰輔助引數。實際上,這一概念相當古老,因為權重衰減是衡量權重大小的一個基本標準。除了單獨使用重量衰減之外,還有許多方法專門為執行稀疏性而設計了懲罰。當前,還有一些方法在權重衰減的基礎之上應用不同的正則化,以期進一步增加稀疏性。
在最近的研究中,有多種方法採用了LASSO(最小絕對收縮並選擇運算子)來修剪權重或組。某些其他的方法還採用了針對弱連線的懲罰,以加大保留引數和修剪引數之間的距離,使它們對效能的影響降為最小。經驗表明,在整個訓練過程中進行懲罰,可以逐步修剪引數,從而達到無縫剪枝的目的。
4 —可用的框架
在神經網路的訓練過程中,無須從頭開始實現(重用論文作者提供的原始碼),在某些現成框架上應用上述基本剪枝方法,實現上相對會更加容易一些。
4.1 — Pytorch
Pytorch為網路剪枝提供了多種高質量的特性,利用Pytorch所提供的工具,可以輕鬆地將掩碼應用到網路上,在訓練期間對該掩碼進行維護,並允許在需要時輕鬆地恢復該掩碼。Pytorch還提供了一些基本的剪枝方法,如全域性或區域性剪枝,無論是結構化的剪枝還是非結構化的剪枝,均能實現。結構化剪枝適用於任何維度的權值張量,可以對過濾器、核心行,甚至是核心內的某些行和列進行修剪。這些內建的基本方法還允許隨機地或根據各種準則進行剪枝。
4.2 — Tensorflow
Tensorflow的Keras庫提供了一些基本的工具來修剪權重較低的引數,修剪的效率根據所有插入的零引入的冗餘來度量,從而可以更好地壓縮模型(它與量化很好地結合)。
4.3 — ShrinkBench
Blalock等人研發了一個自定義庫ShrinkBench,以幫助社群剪枝演算法進行規範化。這個自定義的庫基於Pytorch框架,旨在使修剪方法的實現更加容易,同時對訓練和測試條件規範化。它為不同的剪枝方法(如隨機剪枝,權重大小剪枝或梯度大小剪枝),提供了不同的基準。
5 —結論
綜上所述,可以看出
1)剪枝結構定義了透過剪枝操作可以獲得哪種收益
2)剪枝準則基於多種理論和實際的結合
3)剪枝方法傾向於圍繞在訓練過程中引入稀疏性以協調效能和成本。
此外,儘管神經網路的基礎工作可以追溯到上世紀80年代末,但是,目前神經網路剪枝是一個非常動態的領域,期待有新的基礎理論和新的基本概念出現。
儘管目前該領域百花齊放,但仍有很大的探索和創新空間。每種剪枝方法都試圖回答一個問題(“如何重建修剪後的權重?”“如何透過最佳化學習修剪掩碼?”“如何釋放已經剪去的權重……”),上述所有的研究指明瞭一個方向:貫穿整個訓練過程中的稀疏性。同時,這一方向帶出了許多新的問題,比如:“剪枝準則在還沒有收斂的網路上有效嗎?”, “如何判斷是否剪枝選定的權重會有益於所有稀疏的訓練?”