複合材料力學 致力於複合材料力學與模擬分析領域知識創作與分享! 589篇原創內容 -->
公眾號
1. 導讀
仿生多孔材料,由於其獨特的微結構和較高的機械效能,已被應用於許多領域,並被特別設計用於實現生物醫學植入物和電化學器件的吸能、減重、傳熱和隔熱等功能的材料。近年來,隨著先進製造技術和數字化的發展,3D列印脫穎而出,此技術的發展不僅實現了上述仿生材料特定的微結構,而且透過和拓撲最佳化技術整合,提高啦材料的利用率,縮短了生產週期。基於仿生學和3D列印技術,眾多的研究者透過3D打印製備不同晶格材料、生物多孔微材料、複雜梯度材料來研究仿生多孔材料複雜的力學行為,此類研究已成為熱點話題之一。
但是,在現有的晶格設計研究中,沒有人考慮過微點陣穹頂結構,包括改變其晶格的型別以及不同比強度的多面體單元格型別。鑑於此,東京大學的Jingwei Zhang(第一作者也是通訊作者),在《Composite Structures》上發表了題為“Topology optimization of microlattice dome with enhanced stiffness and energy absorption for additive manufacturing”的文章。
在該研究中,作者提出了一個創新的設計方案:將均勻化拓撲最佳化方法與網格結構相結合,最佳化微點陣的空間分佈,以最大限度地提高微點陣穹頂的壓縮剛度和彎曲剛度以及能量吸收。然後根據拓撲最佳化結果構建三維模型進行CAE驗證和AM製造。最後,透過實驗測試了其在壓縮和三點彎曲作用下的剛度和能量吸收。
2. 內容
2.1 微點陣穹頂模型的設計方法說明
2.1.1 微點陣圓頂的介紹
(1)晶格結構的選擇
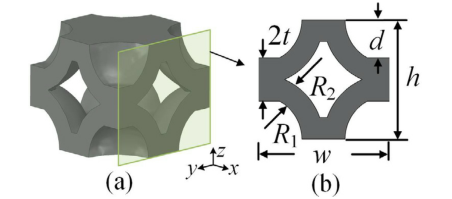
圖1.穹頂的基本單元拓撲結構及其結構引數
(2)微點陣穹頂的概念:不同於蜂窩狀、泡沫狀和格子狀的單元拓撲結構,1/4半球殼的交叉重複佈置構成了穹頂結構的基本拓撲結構,如圖1所示。對於穹頂頂結構,雖然相對密度較高,但其半球形殼體截面具有穩定的剪下響應,有助於抑制核心剪下破壞。此外,面板與芯間的環形接觸面積降低了面板屈曲的風險。圖2可知,實體穹頂變成了多孔微晶格穹頂,減輕了重量,同時允許嵌入體積用於功能部件。透過這樣的組合,輕量化的微點陣穹頂有望比傳統的實體穹頂具有更好的力學效能。
圖2. 微點陣穹頂的設計
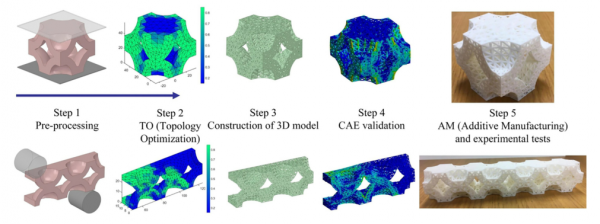
(3)設計流程
圖3. 拓撲最佳化設計流程
2.2 拓撲最佳化
2.2.1 拓撲最佳化問題
最佳化問題一般由目標函式、設計變數和約束條件三部分組成。
2.2.2 設計變數的更新方案
根據最優準則來更新設計變數的最佳化演算法,這是結構最佳化問題的經典方法,並被用於標準拓撲最佳化方法,如SIMP方法。
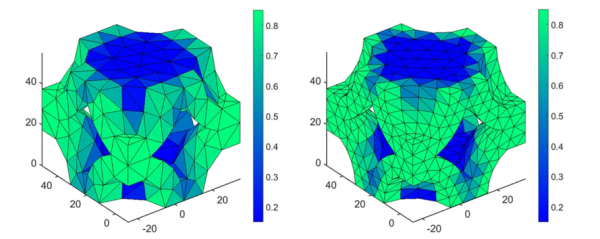
圖4. 由拓撲最佳化得到壓縮模型中晶格的最優密度分佈。
圖5. 由拓撲最佳化得到三點彎曲模型中晶格密度的最優分佈
2.2.3 將拓撲最佳化與微點陣結構相結合
圖6. 由拓撲最佳化生成不同體積分數的六面體單元
2.2.4 拓撲最佳化模型
在本研究中,利用所提出的拓撲最佳化方法來尋找最優的網格分佈,使微點陣穹頂的壓縮剛度和彎曲剛度最大化。壓縮和三點彎曲模型的結構引數如表1所示;其中,壓縮模型的單元格尺寸是三點彎曲模型的兩倍。
壓縮模型的邊界條件如圖所示,頂面施加垂直位移,底面固定。對於三點彎曲模型,如圖所示,在1/4模型的兩個對稱平面上分別施加對稱邊界條件,在上表面中部施加垂直位移。
圖7. 拓撲最佳化模型的邊界條件
2.2.5 拓撲最佳化結果
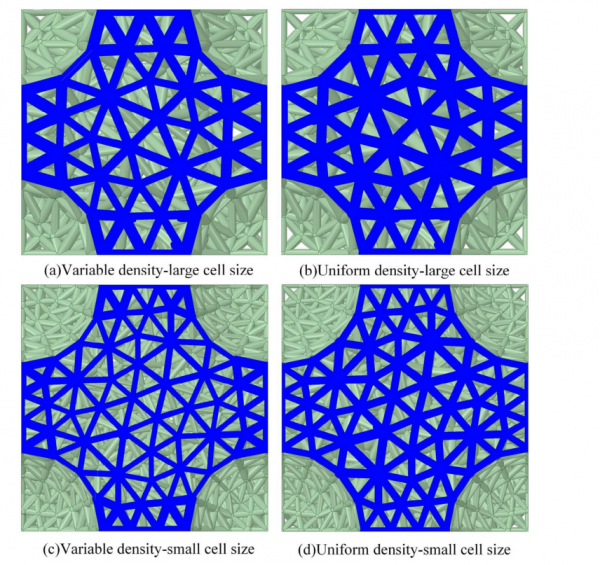
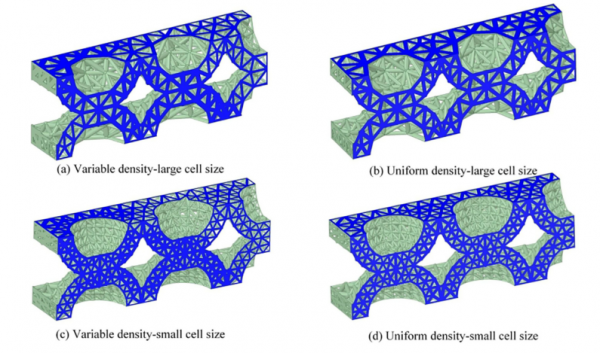
圖8. 構建拓撲最佳化前後不同單元大小的壓縮模型
2.3 微點陣圓頂的構造
2.3.1 構建方法
透過拓撲最佳化得到單元密度分佈後,下一步就是構建三維模型進行數值和實驗驗證。在構造過程中,根據單元的密度生成相應的四面體點陣結構,這就需要建立四面體點陣的結構引數與其密度之間的關係。也就是說,四面體晶格結構的構造可以轉換為在每個節點上生成一個具有相應半徑的球體和在兩個相鄰節點之間生成一個具有相應半徑的圓柱體的操作。因此,只要知道單元密度對應的圓柱體半徑,就可以透過引數化語言在CAD軟體中自動生成四面體晶格結構,如:本研究使用SCDM 2019R1中的python指令碼實現四面體晶格的自動構建。
2.3.2 構建三維模型
圖9. 拓撲前後壓縮模型示意圖
圖10. 拓撲前後不同單元尺寸的三點彎曲模型
複合材料點陣結構力學效能表徵
2.4 數值和實驗驗證
為驗證所提出的設計方法,在整體體積分數為原實體穹頂的50%的,對最小柔度最佳化前後的微點陣穹頂進行了數值模擬和實驗研究。此外,還對實心穹頂的壓縮和彎曲特性進行了數值模擬和實驗測試,並與微點陣穹頂進行對比。
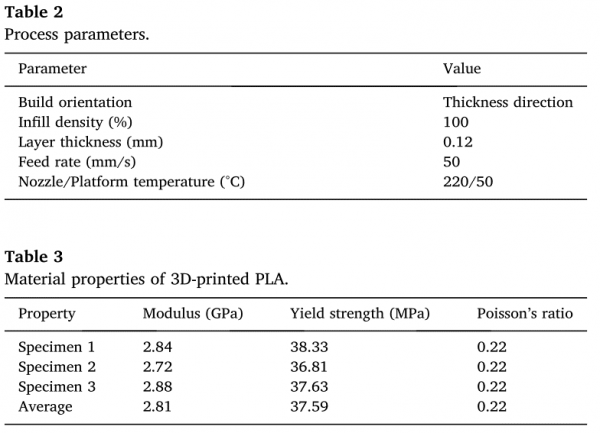
2.4.1 3D列印PLA的材料特性
表1. AM的工藝引數和PLA的材料效能
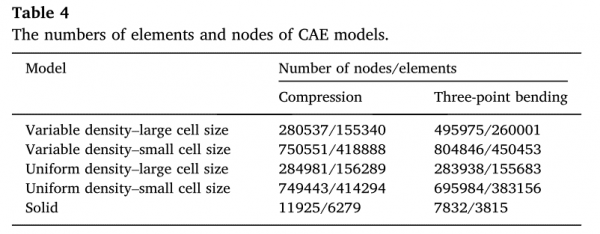
2.4.2 模型資料
表2. 每個模型的晶格數量
2.5 增材製造和實驗設定
採用與列印拉伸試樣相同的工藝引數,打印出最佳化後的模型和未最佳化的實心穹頂。壓縮實驗和三點彎曲實驗的列印微點陣圓頂結構分別如圖12和圖13所示。
圖11. 拉伸試驗試樣設計和結果
圖12. 最佳化前後增材製造壓縮試樣
圖13. 最佳化前後增材製造抗折試樣
2.6 結果和討論
圖14. 試樣壓縮的實驗過程
圖15. 試樣抗折的實驗過程
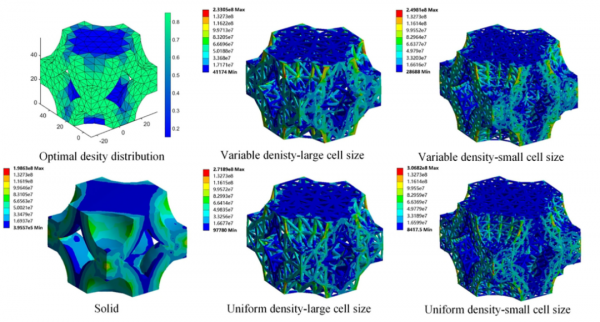
2.6.1 最優密度圖與應力分佈等值線的比較
壓縮模擬和三點彎曲模擬得到的應力分佈圖分別如圖16和圖17所示。透過對比拓撲最佳化得到的密度分佈圖和有限元模型的應力分佈輪廓,發現高密度區域應力較大,而低密度區域應力較小,這是一種透過增加高應力區材料用量和減少低應力區材料用量來增加材料的有效利用率的有效策略。上述結果類似於人體承骨骼,比如承重較小的骨骼,如肩胛骨,往往有一個更開放的內部晶格,而承重較強的骨骼,如股骨,有一個更密集的內部結構。此外,將拓撲最佳化得到的變密度模型的應力分佈圖與未最佳化的均勻密度模型進行比較,發現變密度模型的最大應力低於均勻密度模型。這說明變密度模型的材料分佈更加合理,應力分佈更加均勻。
圖16. 壓縮模擬得到的應力分佈圖
圖17. 三點彎曲模擬得到的應力分佈圖
2.6.2 數值模擬和實驗對比
圖18. 壓縮試驗後微網和實心試樣的斷裂圖
圖19. 抗折試驗後微網和實心試樣的斷裂圖
|
圖20. 數值模擬和實驗得到了三點彎曲應力-應變曲線 |
|
2.6.3剛度和能量吸收
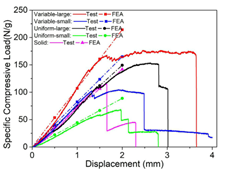
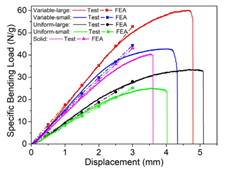
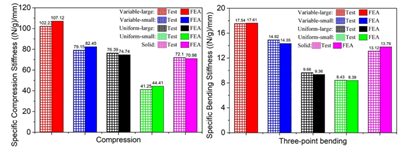
圖21和圖22表明:與未最佳化的模型相比,最佳化後模型的比壓剛度分別提高了33.8%和91.8%;同時彎曲剛度分別提高了81.6%和76.9%;在壓縮模型中,最佳化後的變密度結構大小單元的能量吸收分別提高了72.2%和124.2%。在三點彎曲過程中,最佳化後的變密度模型大大提高了61.8%,減小了33.3%。上述數值和實驗結果表明,所提出的拓撲最佳化方法有效地提高了微點陣穹頂的剛度和能量吸收。此外,最佳化後的變密度微點陣穹頂材料利用率高,比剛度高。與傳統的固體穹頂相比,微點陣穹頂在壓縮和三點彎曲時的能量吸收提高了297.5%和85%。
圖21. 透過有限元分析和實驗得到了比壓剛度和比彎曲剛度
圖22. 試樣的比能量吸收
3. 小結
本文提出了一種新的微點陣穹頂結構,該結構將傳統穹頂結構的實心部分替換為密度較小的部分以及四面體微晶格主導的拓撲結構,確定了微點陣在壓縮和三點彎曲載荷作用下的最優分佈,以最大限度地提高微點陣圓頂的剛度和能量吸收。結果表明,將拓撲最佳化與網格結構相結合,可以設計出具有高質量比剛度和高吸能效能的微點陣穹頂結構。本文所述的均勻化拓撲最佳化和構造方法具有通用性,可用於以微點陣為組成單元的任意宏觀形狀結構的最佳化設計,對超輕超硬結構的發展具有重要意義。
原始文獻:Zhang, Jingwei and Jun Yanagimoto. "Topology Optimization of Microlattice Dome with Enhanced Stiffness and Energy Absorption for Additive Manufacturing." Composite Structures 255 (2021).https://dx.doi.org/10.1016/j.compstruct.2020.112889.