象棋和圍棋都是中華文明的瑰寶,更是訓練和測試思維能力的方式之一,那些在這兩種棋類上取得成就的人們,其智商普遍得到公眾認可。但是,我們是否想過,在這兩種棋類上是否存在必勝或者平局的策略?答案是存在的,這是策梅洛關於雙人完全資訊博弈的一個定理的結論。本文將詳細介紹這個定理的證明,並將其用於諸如五子棋的分析中。如無特殊說明,後文所提及的遊戲都是雙人遊戲。
什麼是最優策略
為了讓大家對最優策略有一個直觀的理解,這裡舉一個小遊戲作為例子。這個小遊戲叫Chop,在遊戲的最開始有一個m×n的網格(下圖是一個4×6網格示例),遊戲由兩位玩家輪流操作,每位玩家每輪可以沿著一整根豎網格線或者一整根橫網格線將網格割掉一塊,割到只剩下一個小方格的玩家為勝者。注意,不能沿著剩餘網格的邊界線做切割,例如不能沿著下圖的AB線切割,但是沿著CD線或者EF線切割都是可以的。每次切割完之後網格會被分成兩塊,由操作切割的玩家決定留下哪一塊。
對於這類雙人遊戲,一般會有最先進行操作的玩家,我們將其稱為先手,另一位被稱為後手。如果一開始的時候m和n其中一個數為1,比如n=1,先手玩家可以直接切割掉(m-1)個格子即可獲得勝利,這個策略就是先手玩家的最優策略。如果對於一般的m和n,先手或者後手怎樣才能保證獲勝呢?讀者可以稍作思考,再接著往下看。
其實很簡單,如果m和n不相等,那麼先手的最優策略會導致必勝的結果:這時候先手玩家只要割掉其中一塊使得剩下的網格是個長和寬相等的網格即可。這樣,無論後手切割哪條線,都是在長和寬相等的基礎上進行切割,最後必然得到一個長寬不相等的網格,也就不可能是單獨一個網格。先手玩家只要每一步實行這個策略,無論後手玩家怎麼操作,先手玩家都會獲勝。這時候讀者肯定明白了,當m=n的時候,無論先手玩家怎麼操作,後手玩家都可以藉助前述一樣的策略獲勝。
完全資訊博弈和策梅洛定理
現在回到一般遊戲的討論上。策梅洛定理適用於被稱為完全資訊博弈的一類遊戲。所謂完全資訊博弈,指的是遊戲的所有資訊都是公開的,遊戲雙方都能清楚瞭解到目前遊戲所處的狀態資訊,並且遊戲的每一步都不涉及機率因素。這個條件把撲克、飛行棋、暗棋和翻棋玩法下的軍棋都排除掉了。然後,我們還需要這個遊戲能在有限步內結束,並且,遊戲的結局要麼是平局要麼有一方是勝者。很明顯,圍棋是屬於完全資訊博弈的。至於象棋,有可能會進入迴圈狀態從而整個遊戲沒完沒了。為了避免這一點,我們可以加入一些新規則使得象棋不會出現迴圈,比如,設定一個很大的數N,只要連續N步雙方都沒有被吃掉棋子就判為和棋,或者不允許超過N次進入同一種棋子狀態,否則判為和棋。加入這些規則或者類似的規則之後,象棋就滿足要求了。
下面給出策梅洛定理的嚴格表述:在雙人完全資訊博弈下,只有三種情況:要麼先手具有必勝策略,要麼後手具有必勝策略,要麼雙方的最優策略會導致平局。比如前面所說的Chop遊戲,當m≠n時,先手玩傢俱有必勝策略;如果m=n,後手玩傢俱有必勝策略。Chop遊戲沒有平局。策梅洛定理是一個結論很強的定理,下面我們會發現,它的證明非常簡單,不需要用到很高深的知識。
策梅洛定理的證明
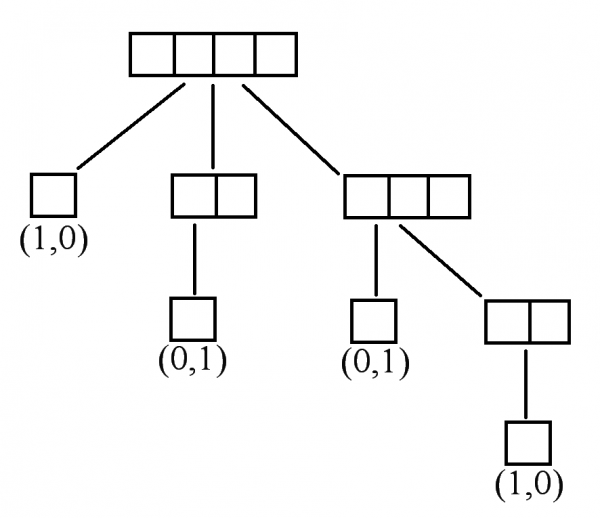
為了證明策梅洛定理,我們需要引入一個小小的概念:遊戲樹。在遊戲的每一步,玩家有很多種走法,每一個走法都會產生新的分支,把兩位玩家的所有可能走法考慮進來,就會得到一個樹狀結構。這個樹狀結構窮盡了遊戲過程的所有可能性。下圖是Chop遊戲在1×4情況下的遊戲樹。在本文,我們用(1,0)表示先手獲勝,(0,1)表示後手獲勝,(0,0)表示平局。
在遊戲樹上,節點會標註上游戲狀態,比如上圖中的方格。有時候為了資訊完全,還會標註上在此節點輪到哪位玩家操作了。因為我們把遊戲迴圈往復的可能性排除了,遊戲狀態轉移圖不會出現圈圖,所以必然是樹圖。(對於象棋,如果用A表示棋子狀態,加上了前文所述的其中一個規則後,整個遊戲狀態將由(A, i)表示,其中i表示已經連續i步雙方都沒有被吃掉棋子或者已經i次進入棋子狀態A了。在這樣的表示下,當i不等於j時,(A, i)和(A, j)哪怕棋子狀態都是A,但是依然代表不同的遊戲狀態。於是,象棋的遊戲轉移也不會出現圈圖。)
接下來,我們假設每一位玩家都是理智的,當玩家處於遊戲樹的某個節點時,她/他必然會選擇對其最有利的走法。假如現在遊戲狀態來到了倒數第二步,再走一步遊戲將結束了,那麼我們就會看到遊戲樹的末端,大概是如下圖這樣的,其中省略號表示未畫出的末端節點
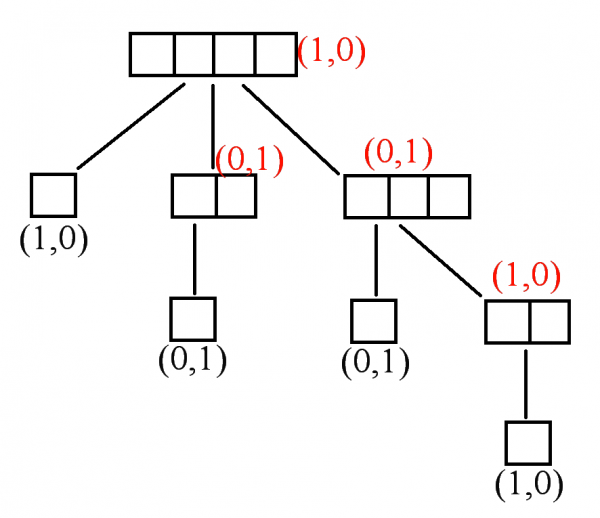
在上圖的遊戲樹中,如果在A處輪到先手玩家操作了,那麼她/他必然會選擇走向B。走向C和D對先手玩家來說都不是最優走法。於是,A雖然不是末端節點,但是它依然可以帶有勝負資訊(1,0),這個勝負資訊表示先手方在A處只要按最優策略走就會獲勝。當然,上圖只是一個例子,有可能末端節點都不是(1,0)狀態的,這時候對先手玩家來說最優策略就是走到平局狀態(如果有平局末端的話),這樣A節點將會帶有(0,0)的勝負資訊。如果是最壞情況,節點A下的所有末端節點都對應(0,1)的勝負,那麼在A處無論先手玩家怎麼走都必輸,於是節點A帶有的勝負資訊是(0,1)。假如我們給勝負引入大小關係:(1,0)>(0,0)>(0,1),那麼前述得到A的勝負資訊的分析可以總結為:輪到先手方操作,A節點的勝負=A的下一級節點的勝負最大值。另一方面,如果在A處輪到後手玩家操作了,我們也可以透過類似的分析得到A處的勝負資訊,只不過最大值要換成最小值:輪到後手方操作,A節點的勝負=A的下一級節點的勝負最小值。
得到了A處的勝負資訊之後,我們就可以忽略A下面的所有節點了,這時候A就成了一個末端節點,它帶有相應的勝負資訊,這個勝負資訊表示從該節點出發,兩位玩家都使用最優策略後會導致的勝負結局。這個操作可以繼續進行下去,不斷得到上一級節點的勝負資訊,然後忽略掉舊的末端節點。如此往復,因為樹是有限高的,最終我們會得到遊戲一開始那個節點(術語叫根節點)的勝負資訊。如果根節點的勝負資訊是(1,0),那麼意味著先手玩家只要按最優策略走下去就會必勝;如果根節點的勝負資訊是(0,1),那麼意味著後手玩傢俱有必勝策略;如果根節點的勝負資訊是(0,0),那麼意味著雙方的最優策略會導致平局。至此,策梅洛定理證明完畢。
從下往上的勝負資訊推導
如何確定誰才具有必勝策略:策略竊取
想必讀者已經躍躍欲試了,如果知道了象棋或者圍棋的最優策略,豈不是在棋壇上橫著走?可惜的是,雖然策梅洛定理的證明是構造性的,但是構造過程需要我們先得到整個遊戲樹,而像圍棋這類棋,遊戲的路徑(指從根節點到末端節點的一條路徑)比宇宙的原子數目還要多,要想透過整個遊戲樹來得到最優策略是不可能的了。如此說來,策梅洛定理僅僅給必勝或者平局策略提供了存在性。不過,藉助策梅洛定理所提供的存在性,我們可以利用被稱為策略竊取的方法證明在某些遊戲上後手不存在必勝策略,換言之,先手有不敗策略。
本文將以著名的五子棋為例介紹策略竊取是怎麼一回事。很明顯,五子棋滿足策梅洛定理的條件,於是有且僅有三種可能性:先手具有必勝策略、後手具有必勝策略、雙方的最優策略會導致平局。接下來我們使用反證法。假如後手具有必勝策略,我們把這個策略稱為S。這時候無論先手玩家怎麼走,後手玩家只要使用策略S,先手玩家必輸。
策略竊取的要點就是把對方的策略“竊取”過來。先手玩家先在棋盤上隨便放一個棋子,位置記為P1,然後假裝這個棋子不存在。這時候輪到後手玩家放子了,由於假裝P1上的棋子不存在,後手玩家成了“先手”,而先手玩家成了“後手”,於是先手玩家可以使用必勝策略S。根據這個策略的必勝性質,無論對方怎麼走,“後手”玩家(也就是先手玩家)都將獲勝。不過,事情似乎沒那麼簡單。我們只是假裝P1上的棋子不存在而已,實際上這個棋子是存在的。P1位置上的棋子會怎麼影響到策略S的使用呢?假如走到了某一步,策略S要求“後手”玩家將棋子放在P1位置,這時候P1已經存在“後手”玩家的棋子了,但是遊戲要求玩家每一步都不能不下棋子,此時“後手”玩家可以在這一步把棋子下在其他的任意位置,記為P2。這樣的話P1和P2都佔據了“後手”玩家的棋子,這就等價於遊戲一開始“後手”玩家將棋子下在了P2,並且在目前這一輪“後手”玩家根據策略S的要求把棋子下在了P1位置。如果接下來策略要求棋子下在P2,那麼“後手”玩家可以任意把棋子下在P3位置……如此類推,先手玩家可以完美使用策略S,於是會必勝。這和反證法的假設相矛盾。於是,五子棋只能存在兩種情況:先手具有必勝策略、雙方的最優策略會導致平局。或者更簡潔地表述為,先手具有不敗策略。
回顧前述關於五子棋的討論,這個“五”字完全沒有體現出來,我們完全可以把相關結論推廣到四子棋、六子棋等等。特別地,井字棋本質上是一種三子棋,由於它的遊戲樹很簡單,我們甚至可以透過窮舉法證明在井字棋上確實是先手玩傢俱有不敗策略。
在哪都能玩的井字棋
轉載內容僅代表作者觀點
不代表中科院物理所立場
來源:中科院理論物理研究所
原標題:DoctorCurious 26: 什麼?象棋和圍棋都存在不敗策略?
編輯:藏痴