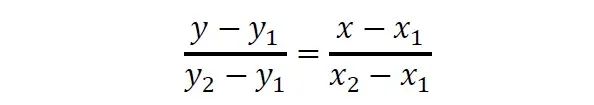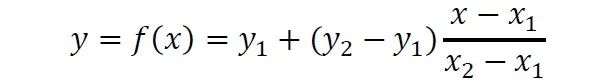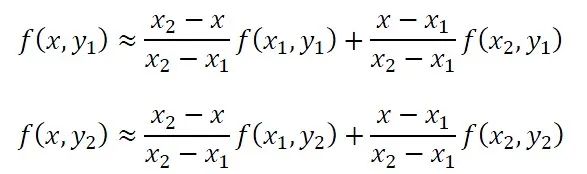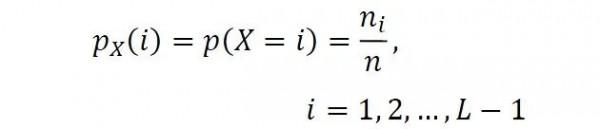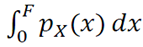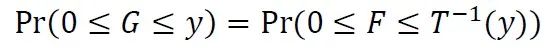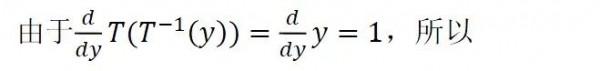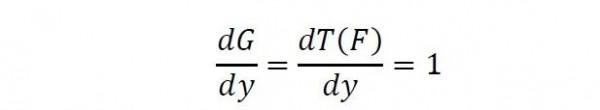編者按
盼望著,盼望著,期末來了,考試的腳步近了……
為了表示對期末黨的關愛,今天小編安排了動漫題材,希望大家都能順利透過考試。
不考試&不看動漫的三元人士也不用失望,扒開本文二次元的偽裝,您依然可以看到熟悉的硬核知識~
前幾日,小編在取材(摸魚)的時候,無意間竟然發現新一集《博人傳:火影忍者新時代》的標題——
作為一名出生於上世紀的老二次元,筆者滿懷期待地點開影片,然而……
這竟然就是第一場考試的全部內容……
(圖片來源:iqiyi)
小編默默關上了影片,心中更是五味雜陳——是時候讓這些年輕人感受真正的忍道啦!所以,這篇文章就是教大家如何科學地透過中忍選拔考試。
中忍選拔考試簡介
中忍考試,顧名思義,是下忍(低階忍者)升為中忍(中級忍者)的考試,一年舉行兩次。綜合《兵之書》、Narutopedia、Boruto Wiki等資料,可知雖然每屆考試試題及形式可能會因為考官不同而有所差異,但基本的模式是相似的。本文將以《火影忍者》第一季漩渦鳴人首次參加考試為背景,為大家簡單回顧中忍考試的基本情況。
考試內容:9道題+1道附加題,檢驗考生的偵察能力——允許作弊,但必須瞞過監考老師,被抓到5次被淘汰。
顯而易見,有大量考生在第一輪筆試中就慘遭淘汰。所以要想在之後的考試中大展身手,最為關鍵的就是要透過第一場筆試的考驗,這也是區分路人和主角的重要階段。
考場上各顯神通的忍者們
(圖片來源:youku.com)
針對考生考試中表現的分析可知,有些考生獲取答案的方式較為特殊,不太適宜大範圍推廣(譬如寧次、佐助利用血繼限界這需要拼爹;又如牙、志乃需要特定“忍具”的協助攜帶寵物入考場)。
相比之下,我愛羅同學的手法(利用仿生學技術製造眼球)比較貼近現實,但獲取的影像尺寸較小且清晰度不足(可能與製造眼球的材料是沙子有關)。因此我們接下來將探索如何才能獲取清晰的試卷影像。影象處理的演算法博大精深,包羅永珍。這裡針對我愛羅獲取影象尺寸和清晰度的特點,主要介紹影象放大和影象增強演算法。
上圖:我愛羅用沙子製成仿生眼球
下圖:我愛羅獲取的試卷影像,並不十分清晰
(圖片來源:youku.com)
“比更大還更大”——插值法
影象不清晰的首要原因是影象不夠“大”。但是在日常生活中我們都會有類似的體驗,點陣圖在放大後質量會明顯下降。因此不能簡單地透過修改尺寸的方法來放大點陣圖。為了保證點陣圖放大之後的影象質量,需要我們在畫素陣列中插入一定的值,保證放大後的陣列不至稀疏。
小知識:點陣圖指的是使用畫素陣列表示的影象。相對應地,基於數學方程的幾何圖元表示的影象被稱為向量圖。換言之,向量圖是“算”出來的,所以放大之後質量不會下降。而點陣圖是陣列“擺”出來的,放大將使得陣列變得稀疏,從而影響圖片質量。
點陣圖vs向量圖
一個簡單的思路就是,選擇距離所求資料點最近點的值,同時忽略其他相鄰點,從而產生一個分段常數的內插值來作為所求資料點的值,即所謂最近鄰插值法。該演算法實現起來非常簡單,但由於忽略了其他相鄰資料點的資訊,所以效果也略遜於其他演算法。
另一個顯而易見的思路是,假設相鄰兩個畫素的值都位於這兩個數值所確定的直線上,而這種方法也就是所謂的線性插值法。方法的思路十分簡單,基本可以藉助初中的數學知識來實現。
線性插值法
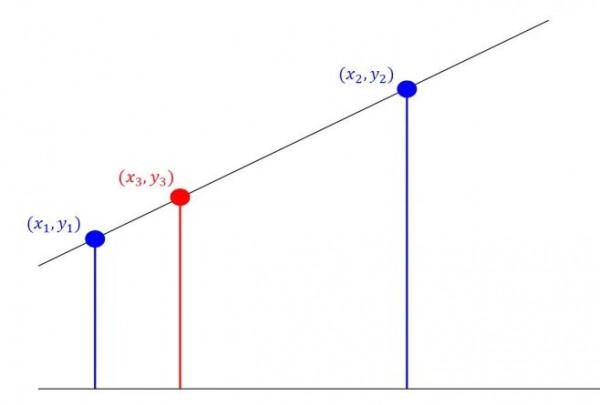
方法的思路十分簡單,基本可以藉助中學的數學知識來實現。已知兩點(x,y)與(x,y)的具體值,求區間[x, y]內某一位置x對應的值y。假設x與y滿足函式y=f(x),f(x)的表示式並不確定。如果兩點的距離不遠,我們不妨假設此時(x,y)與(x,y)滿足直線方程的表示式,利用真·高中數學知識(直線方程兩點式)可得
稍作處理
給出x3的值,就可以很容易地求出y3。
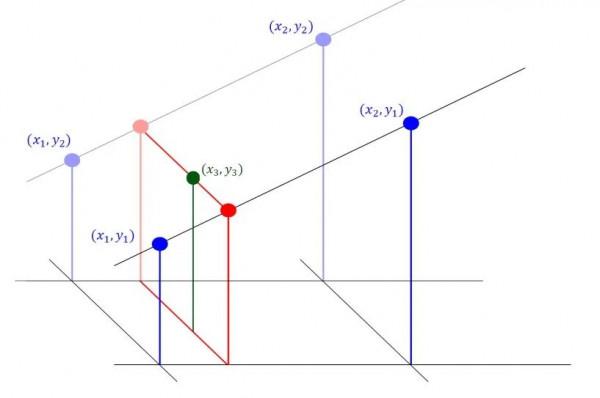
對於實際的二維影象,情況會稍微複雜一些,但本質上也是上面線性插值法的擴充套件,即所謂的雙線性插值法。雙線性插值法的核心思想是在兩個方向分別進行一次線性插值。
雙線性插值法
下面的推導過程,學有餘力的同學可以點開
點選展開
推導過程
假設影象Z可以表示為函式z=f(x, y)的集合,其中(x, y)代表某個畫素的位置,z代表這個畫素的色彩值。譬如已知(x,y),(x,y),(x,y)和(x,y)四個點,我們可以套用上面的方法求得區域內(x,y),也就實現了插值。具體而言,先考慮x方向的線性插值,有
然後考慮y方向
稍微處理一下,可以讓公式更好看一點
當然,我們可以參考線性插值法的思路更進一步,利用非線性函式進行插值,以提高放大後圖片的品質。例如前面提到的幾種方法中,雙三次插值的效果一般優於另外幾種方法,一方面三次函式本身較其他幾種函式更具優越性,另一方面雙三次插值採集了插值點附近16個點的資訊(多於二維最近鄰、雙線性的4個取樣點和雙二次的9個取樣點),也就可以更好地體現影象的細節。
Jerry親自示範如何在人群中運用插值演算法
(圖片來源:bilibili.com)
獲得更多細節——影象增強
當然,對於很多影象來說,僅僅放大仍然不足以為我們提供足夠的細節,這時候我們就需要透過其他演算法以實現影象增強(如提高影象的對比度,突出影象的輪廓/銳化等)。
圖片來源:qq.com
實現影象增強的演算法有很多,需要根據具體的應用場景加以選擇。此處根據我愛羅獲得影象的特點,嘗試增強圖片的對比度。一般而言,一個影象的對比度不足,往往是由於影象畫素強度(或者通俗點說,每個點顏色的深淺)過於集中導致的。處理的思路也非常簡單粗暴,就是透過一定的變換,將原本集中的畫素強度分散開來。理想狀態下,變換後圖像畫素強度的機率密度呈均勻分佈,而這也就是直方圖均衡化演算法的內在邏輯。
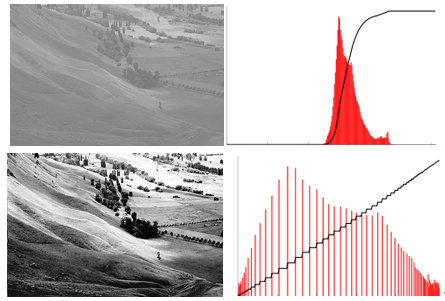
原圖(左上)vs 直方圖均衡化(左下)
圖片來源:Wikipedia
右側為對應圖片的直方圖(紅)及累積分佈函式。顯然,直方圖均衡化之後的影象變“亮”了許多,山上的樹木變得清晰,山坡的紋理也得以顯現。
下面的具體推導過程,學有餘力的同學可以點開
點選展開
推導過程
具體而言,如果我們用代表原影象,設定影象為8位深度(圖中每個畫素顏色所佔的二進位制位位數),所以畫素強度共有=2=256級。假設為畫素強度出現的次數,為影象所有畫素數。那麼原影象歸一化的機率分佈直方圖()
變換後圖像的累積分佈函式g寫作
於是我們可以定義變換,= (),則有
這裡不妨假設()與()分別為與對應的連續變數,且,∈[0,−1]。對於連續變數而言,變換同樣成立=(),那麼有
為了簡化問題,假設變換可微且可逆,顯然有
即
其中為的機率密度函式。運用複合函式求導法則,
同時
所以
即我們期望得到的均勻分佈的機率密度函式。換言之,變換就是我們的目標變換。
數值模擬——從理論到實踐
上文粗略地介紹了幾種演算法的思路和基本原理,接下來,我們將理論應用於實戰之中,藉助python的OpenCV庫來實現前述的各種演算法。當然有興趣的讀者也可以嘗試使用其他語言來實現(譬如Matlab就直接內建了函式interp1和interp2來處理一維和二維插值問題)。
首先我們來測試插值法。本文主要測試最近鄰插值演算法、線性插值演算法和三次插值演算法。考慮到手機端的呈現效果(不會吧,不會吧,不會真的有人用電腦刷微信公眾號吧?)這裡我們只選取了我愛羅視野中的部分資訊,然後分別利用三種演算法,長和寬都擴大為原來的15倍,效果如下
最近鄰插值演算法(左)、線性插值演算法(中)和三次插值演算法(右),右下角小圖為原始影象
(點選圖片放大看更清晰哦)
顯然,經過最近鄰插值演算法放大的影象,邊緣出現了明顯的鋸齒。而利用(雙)線性插值和(雙)三次插值演算法處理的影象邊緣比較平滑,沒有出現明顯的鋸齒形狀。
接下來,我們測試幾種常見的影象增強演算法。首先我們直接在原始影象上使用直方圖均衡化演算法,此時我們得到的影象如下:
直方圖均衡化
顯然,直方圖均衡化的表現不夠理想。主要原因在於一般的直方圖均衡化演算法使用從影象直方圖匯出的相同變換來變換所有畫素。這對於畫素值分佈相似的影象較為有效,但對於紙卷這種部分內容(如字跡)明顯比大部分影象更深暗的區域,這些區域反而無法得到充分的增強。當然要改善這種情況,一個思路就是利用前文的插值演算法對影象進行預處理。
雙三次插值預處理後的直方圖均衡化
上圖在使用直方圖均衡化前,首先利用雙三次插值演算法處理原影象。利用插值演算法使整張圖的畫素分佈更為均勻。當然我們也可以使用限制對比度自適應直方圖均衡化(CLAHE)演算法,每個畫素都根據畫素周圍影象的直方圖進行變換,同時限制放大的程度,從而減少噪聲也被放大的問題。
限制對比度自適應直方圖均衡化
當然,除了上述提到的演算法之外,讀者朋友們也可以選擇直接運用數理化知識,把題目解出來。
彩 蛋 時 間
話說我愛羅到底看到了哪一道題呢?
經過相關演算法進行影象處理後得到的影象
“大人,時代變了!”
圖片來源:youku、zhihu@無妄之神
轉載內容僅代表作者觀點
不代表中科院物理所立場
原標題:學習不好都看不懂動漫了——論如何科學地透過忍者考試
來源:科學大院
編輯:just_iu