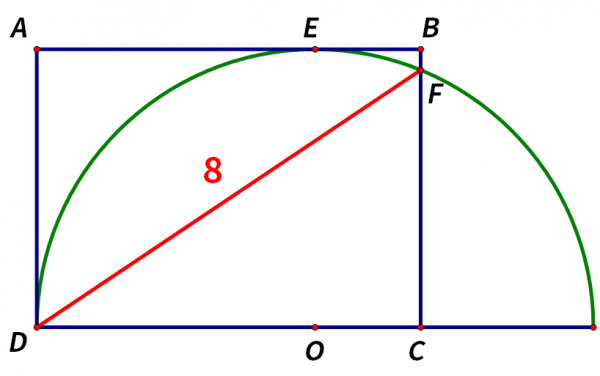
如圖,已知四邊形ABCD為矩形,矩形ABCD和半圓O相切,切點為點E、點D,半圓O和BC相交於點F,連線DF,DF=8,求矩形ABCD的面積。這道題怎麼做呢?
我們要求矩形ABCD的面積,就需要知道矩形的長和寬為多少。
我們不妨假設AB=x,AD=y,我們要求的是xy。
接下來就是找等量關係,構造方程了。
矩形ABCD和半圓O相切,切點為點E,連線OE。
OE垂直AB。
四邊形AEOD有3個內角為直角,且OE=OD,所以四邊形AEOD為正方形。
OE=OD=AD=y,OC=x-y,
在直角三角形CDF中,DF=8,
由勾股定理,可得CF²=DF²-DC²=64-x²,
現在已經有了1個方程,但是1個方程是不夠的,我們還需要再建立1個方程,
連線OF,
在直角三角形OCF中,CF²=OF²-OC²=y²-(x-y)²,
所以CF²=64-x²=y²-(x-y)²,由這個等式可得xy=32。
矩形ABCD的面積=32。
以上就是這道題的解法,除此之外,你還有其他方法嗎?可以在評論區留言~