同等周長下，圓面積最大，此定理為何人類用了幾千年才得以證明

為什麼在同等周長的所有圖形當中，圓形的面積是最大的呢？為什麼在所有等面積的立體之中，球體的體積是最大的呢？

這個問題看起來好像是很簡單，但實際上證明起來非常麻煩，人們證明這個定理證明了兩千多年。那我們就一起研究一下這個問題。

從古代開始說這個問題

對於圓形面積大這件事，最早的應用應該是在公元前814年。有一個國家建立了，名字叫迦太基國，大家可能聽說過，意思是 “一張牛皮”。

傳說迦太基是現在的突尼西亞的位置，在迦太基國建立之前，有一個古老的國家。這個國家裡面有一種人叫腓尼基人，他們是西亞的人，並且國家內斷了。於是有一個國王的姐姐或者是一個公主，她帶著族人來到了突尼西亞。到了突尼西亞之後，她想向當地的人買一塊地皮，然後送給當地人很多禮物。

但是當地人不賣，她就說我只要一塊牛皮能夠圍起來的面積就可以了，當地人一想一塊牛皮能有多大，於是就讓她圍。沒想到她把一塊牛皮剪成了很多個小條，然後在海岸這兒圍成了一個半圓形。

我們可以想一下，如果剪的非常細的話，這個面積就很大，於是就在這個地方建立了一個國家一一迦太基。後來發展的非常強大，成為當時和希臘並行的地中海沿岸最強大的國家，不過最後被羅馬滅掉了。這個應該就是人們對於圓形面最大的最早的應用，那麼為什麼圓形的面積最大呢？這個我們稱之為等周定理。

等周定理是什麼？

等軸定理是說在周長一定的平面圖形之中，圓形的面積最大，這個就是等周定理。

最開始的時候，人們並沒有證明出這個定理，但是都在不停地使用它，而且沒有人懷疑這個定理是有問題的，因為它確實是對的。

芝諾多羅斯的證明

那麼最早嘗試去證明的人是一個古希臘的數學家，名字叫芝諾多羅斯。他去證明這定理的時候，分了幾個步驟。

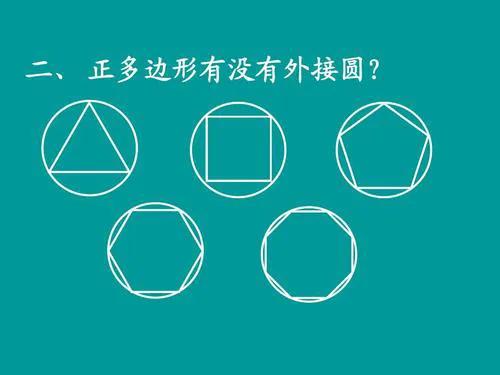
第一他證明了在等周的多邊形中，正多邊形面積大。也就是說在等周長的情況下，正四邊形比非正四邊形的面積大，而正五邊形比非正五邊形的面積大……正多邊形面積大，這是第一個要證明的。

第二，在同樣等周的正多邊形中，邊數越多面積越大。

舉幾個例子，比如說正多邊形以三角形為例。一個三角形它必須周長一定，我們假設周長是1，每個邊邊長是1/3。我們知道三角形面積公式是S＝（低x高）/2，所以這個面積大約為0.04811。

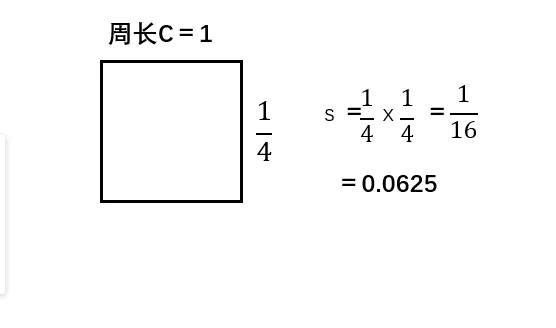
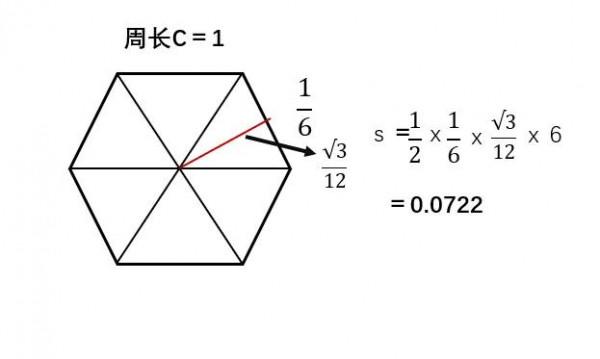
假如周長為1的圖形變成一個正方形呢？正方形的邊長為1/4，面積是1/16，就是0.025。從正三角形變正四邊形，它面積顯然變大了。正五邊形不好算，看一下正六邊形。正六邊形可以分割成六個正三角形，每個正三角形邊長都是1/6，一共有六個，這個數它等於0.0722。

按照這個規律去找，正多邊形面積比非正多邊形面積大。而正多邊形之中邊數越多，面積越大，如果把邊數無限變多不就變成一個圓形了。所以就是說在周長一定的時候，圓形的面積最大，周長一定圓形面積是最大的。

如果周長是1圓形的，面積有多大？顯然面積這個數大約為0.07985。圓形的面積比正多邊形都大，但是他這個定理證明的問題很大。尤其是最後一步，從正多邊形要推出圓，看起來好像是一小步，但實際上中間涉及到一個極限的變化。而在那個時代，人們對於極限無窮角小都很不清楚，所以這種證明人們認為是非常不嚴格的。

那麼在中世紀的時候，數學也沒什麼發展，再往後的時候呢，人們又去研究很多奇怪的數學問題，沒有人去證明它，包括高斯尤拉都沒有去證明。直到近現代，人們才真正地給出了這個定理的證明。

雅可布斯坦納的證明

近現代這個問題在1893年的時候，有一個德國數學家叫雅可布斯坦納，

他被譽為是歐幾里德以來最偉大的幾何學家，他幾何非常厲害，給出了這個定理的第一個證明，真正意義上的證明。他也分了三步！

第一步說如果存在一個面積最大的圖形的話，這個面積大圖形一定是凸的，一定是外凸的。簡單說明一下，隨便畫的一個圖形，它中間有一個凹陷，那這個圖形肯定不是面積最大的，為什麼呢？

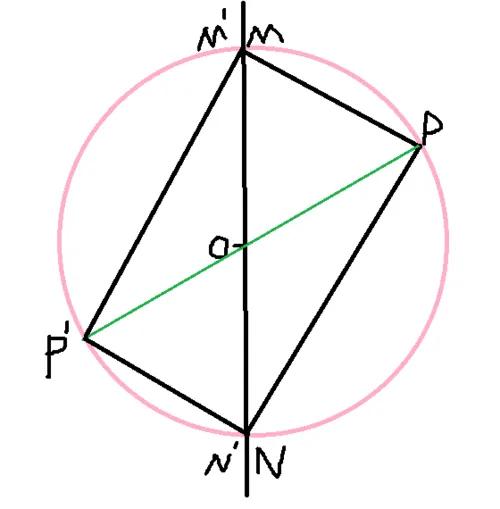
因為在周長一定的情況下，我們把這兩點連起來，這叫a和b，然後我們以a b 這條線為對稱軸，把底下凹進去這一塊讓它鼓起來，得到新的圖形，這兩個圖形周長一樣但是面積卻變大了。所以如果面積最大，它不可能出現凹陷的情況，它一定是往外凸的。這是第一條。第二條圖形面積是最大時，存在平分周長的弦，那麼它也一定平分面積。為什麼呢？比如畫一個圖形，假如這個圖形面積是最大的，然後有了一根弦ab它平分了周長，兩半周長都是原來一半的周長。但是面積不一樣可以嗎？

答案是不可以！這裡用反證法。假設兩邊兒周長一樣都是1/2周長，但是面積不一樣，一個是S1，另一個是S2。我們讓S1小於S2，那麼我們完全可以讓總面積更大。把S2對稱過去做一個S2關於a b 的對稱圖形面積變大了，同時周長是一樣的。在周長不變的前提下面積還可以變大，跟圖形面積是最大相悖。因此平分周長的弦，那麼它也一定平分面積！

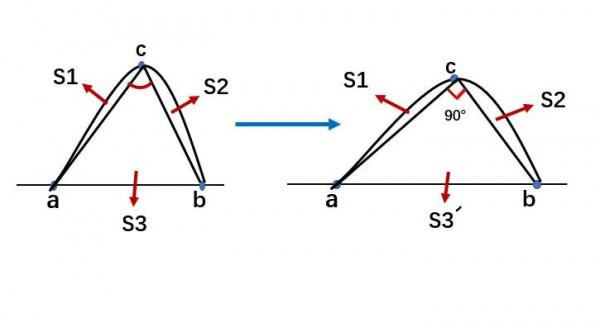
第三條，假如有一個直線，然後有一個a 和b 兩個點，兩個點都在一條直線上，畫一個曲線。如果說這個曲線與線段ab圍成圖形面積最大，那這個圖形一定是個半圓。為什麼是這樣呢？在曲線任意找一個點c，連線ac，bc，這樣就把這個圖形分成了三個部分，分別為S1、S2和S3；且角acb不等於90°。現在我們做這樣一個工作，就是保持S1、S2不變，但是三角形S3變為直角三角形。

這個過程中ac和bc不變，所以直角三角形面積最大原因是因為它高線是最長的。因此在面積最大的時候，它一定是一個半圓。這三條綜合起來，我們就可以證明一定是圓形面最大了。因為做兩個半圓把它一拼，那就是個圓兒了。

數學家的質疑和其他證法

不過也有一些數學家對他有一些質疑，什麼質疑呢？這一切的前提是存在性，就是所要的這個的面積最大的圖形，它是存在的。它如果存在，它就一定是個圓兒。但是並沒有證明它存在性。這就是數學的美妙之處，你認為這已經非常合理的，數學家認為它不合理，於是人們繼續去找證明。

在1870年德國數學家，名字叫威爾斯特拉斯，他第一次對這個定理進行了嚴格的證明，而他使用了變分法。變分法是一個比較高超的數學技術，把這個問題進行了嚴格的證明；再後來又有一些其他數學家用其他的方法把這個問題證明出來了。還有人證明了三維情況的等周問題，就是說同樣的表面積的所有的立體當中，球的體積是最大的，這就是三維情況等作問題。