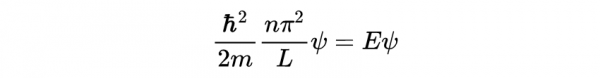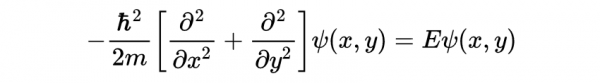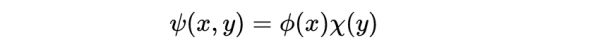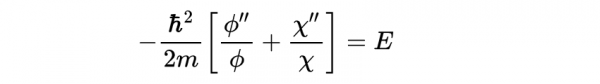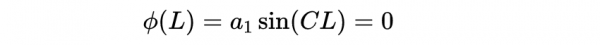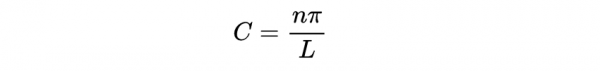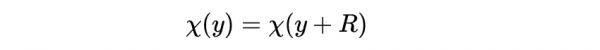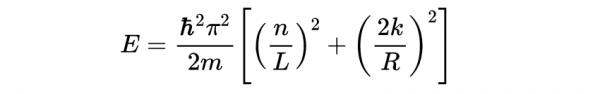弦理論是統一量子力學、引力和廣義相對論的主要科學成果之一。這個理論帶來了驚人的預測,最引人注目的是,我們生活在一個更高維度的世界,而不是一個三維世界(相對論是四維時空)。
根據弦理論的不同,額外維度的數量也不同。然而,這些額外的維度在哪裡呢?到目前為止還沒有人注意到它們。這就是我們的弦理論嗎?顯然不是,否則,成千上萬的物理學家不會把他們的一生奉獻給這個物理學分支!
在本文中,我想讓這些想法更具體一些。我們將看看“上帝的主方程”之一,薛定諤方程,並把它應用到“玩具”世界。這讓我們看到,捲曲的額外維度有什麼影響,以及我們如何觀察它們。
薛定諤方程(沒有額外維度)
我們的“玩具”世界只有一維,一個縮小版的平面。它向兩個方向無限延伸。這個玩具世界的薛定諤方程式是這樣的
其中()為系統的勢能函式,為總能量。讓我們進一步假設把一個粒子困在一個很小的體積裡,比方說在=0和=之間。我們以某種方式把它控制在這個區域,它可以在那裡自由移動,但它無法逃脫。這可以用勢能函式來描述
所以薛定諤方程化簡成
邊值條件是
否則薛定諤方程就不能在勢能無限的區域中得到滿足。在這種情況下,薛定諤方程簡化為諧振子的形式,滿足邊界條件的解為
其中是一個≥1的整數,是某個常數。把它插入薛定諤方程中就得到了
或者
所以粒子有一個離散的,儘管有無限個允許的能級。越高,能量越高。沒什麼特別的。
額外的捲曲維度
額外的捲曲維度?如果你用實數線表示一個標準維度,那麼這個維度在兩個方向上都無限延伸。捲曲,或者用技術術語來說:緊化,意味著我們將那些相距距離的點定義為相同的點。所以當你沿著這條軸移動一段距離,你會在你開始的地方結束。我們所做的就是把這個維度變成一個圓圈,這就是為什麼人們叫它捲曲的維度。
假設在“玩具”世界中,除了正常的維度外,還有一個額外的捲曲維度我們稱這個方向的座標為。假設我們捕獲了一個粒子在-space的同一個區域。那麼
我們可以很容易地用分離方法將這個偏微分方程轉化為常微分方程
代入薛定諤方程得到
其中,上標符號分別表示對單個變數或的導數。除以:
也可以寫成
注意,這裡的左邊是的函式,而右邊不是。右邊是關於的常數。我們稱這個常數為-^2。然後,乘以,我們可以將方程寫成
這就是諧振子的方程,它的通解是
同樣的論證也適用於,但這次是針對,而不是。在這個例子中表示常數,我們有
讓我們在邊界條件下固定一些常數,得到
此外,我們有
因為_1不可能是零(這意味著=0,這意味著根本沒有粒子),我們必須有
對於(),唯一的邊界條件是維度是捲曲的,所以
這意味著常數必須具有正確的大小,使週期等於:
其中≥0為整數。
總之,我們有了波函式的解
將解代入薛定諤方程,就可以得到允許的能量
這取決於和。=0是允許的,所以在這種情況下,變化的能量是相同的,沒有額外的維度。但是透過>0,我們可以獲得額外的能量級別!為什麼我們還沒有觀察到呢?
因為,如果非常小,那麼來自額外維度的能量項是巨大的。所以,在這種情況下,任何來自額外維度的能級,只有在非常高的能量時才會可見。如果真的很小,那麼所需的能量是如此之高,以至於我們目前的技術無法觀察到。但也許,在未來的某一天,我們可以做到。