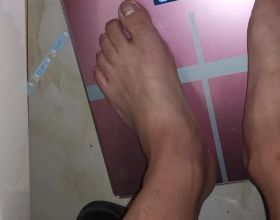
- 研究人員長期以來一直在研究重力是如何從二維曲面中出現的,比如這個雙曲空間。在我們的宇宙中,表面是無限的。
自從牛頓遇到蘋果以來,我們就已經知道了萬有引力,但我們仍在努力弄清楚它的意義。其他三種自然力(弱核力、強核力、電磁力)都是由於量子場的活動產生的,而物理學最成功的理論之一(相對論)將引力描述為彎曲的時空(引力即幾何)。幾十年來,物理學家一直試圖用量子場論來描述引力,但都沒有完美地解決這個問題。
這些“嘗試”中最有希望的一種是將引力視為某種類似全息圖( hologram)的東西——一種從平面二維表面跳出來的三維效果。目前,這種理論的唯一具體例子是AdS/CFT對應,其中一種特殊型別的量子場論,稱為保角場論(CFT),在所謂的反德西特(AdS)空間中產生了引力。在AdS空間奇異的曲線中,有限的邊界可以封裝無限的世界。該理論的發現者胡安·馬爾達塞納稱其為“瓶子裡的宇宙”。
但我們的宇宙不是一個瓶子。我們的宇宙(很大程度上)是平的。任何能容納我們扁平宇宙的瓶子都必須在空間和時間上是無限遙遠的。物理學家稱這種宇宙為“天球”(一個想像假設的無限大球體)。
物理學家想要確定CFT的規則,CFT可以在沒有AdS空間曲線的世界中產生引力。他們在尋找平坦空間的CFT——天球中的CFT。
天球中的CFT比相應的AdS/CFT理論更有野心。由於它在一個無限半徑的球體中,空間和時間的概念就不成立了。因此,CFT不依賴於空間和時間;相反,它可以解釋空間和時間是如何形成的。
最近的研究成果給了物理學家們希望,他們的研究方向是正確的。這些結果使用基本對稱性來約束CFT可能的樣子。研究人員在這些對稱性之間發現了一組令人驚訝的數學關係——這種關係之前在某些弦理論中出現過,這導致一些人懷疑這種聯絡是否不僅僅是巧合。
球體的對稱性
也許物理學家探測自然基本力的主要方法是將粒子碰撞,看看會發生什麼。術語叫作“散射”。在大型強子對撞機等裝置中,粒子從遙遠的地方飛進,相互作用,然後飛向探測器。
如果這種相互作用是由除萬有引力之外的這三種力中的任何一種控制的,物理學家們原則上可以用量子場論計算出這些散射問題的結果。但許多物理學家真正想了解的是引力。
幸運的是,史蒂文·溫伯格在20世紀60年代指出,某些量子引力散射問題——涉及到低能引力子的問題——是可以計算出來的。哈佛大學的莫妮卡·佩特說,在這種低能量極限下,“我們已經鎖定了這種行為。”
量子引力再現了廣義相對論的預言。
它們透過尋找對稱性來做到這一點。在散射問題中,物理學家計算散射的產物——“散射振幅”——以及當它們撞擊探測器時應該是什麼樣子。在計算出這些振幅之後,研究人員尋找粒子在探測器上形成的模式,這些模式對應於散射過程必須遵守的規則或對稱性。對稱性要求如果對探測器應用某些變換,散射事件的結果應該保持不變。
正如量子相互作用可以轉化為散射振幅,從而導致對稱性一樣,研究量子引力的研究人員希望將散射問題轉化為天球上的對稱性,然後使用這些對稱性來填充天球中的CFT規則手冊。
11月,哈佛大學的Andrew Strominger領導的一個小組發表了一篇論文,描述了天球中CFT必須遵守的“對稱代數”。代數規定了不同的對稱變換如何結合形成新的變換。他們發現,天球上的一組對稱服從一種代數,這種代數已經出現在某些弦理論中,與量子系統(如量子霍爾效應)有關。
無限的問題
當理論適用於一個無限的球體時,問題就出現了。考慮兩個粒子在一起又分開。如果它們以任何非零的角度分散開來,當它們到達無限大的天球時,它們也會相距無限大。
距離的概念被打破了。我們的正常理論依賴於區域性性,在區域性性理論中,物體之間的相互作用的強度取決於它們彼此之間的距離。但是,如果一切都與其他一切無限遠,CFT必須超越區域性性。
更令人困惑的是:天球上的時間概念是什麼,在過去和未來都是無限遙遠的?在這裡沒有意義。
資料來源:quantamagazine