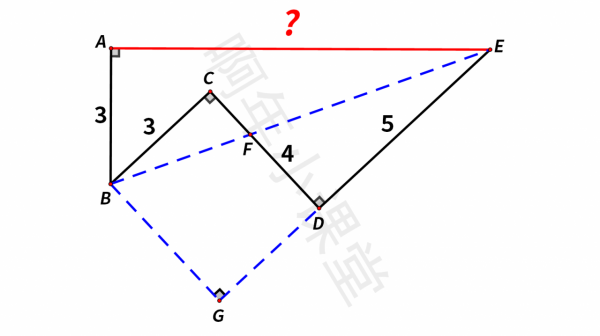
如圖,AB=BC=3, CD=4, DE=5,∠A=∠C=∠D=90°,求AE的長。這道題怎麼做呢?
這道題我們可以採用逆推的方法,我們要求AE的長度。
已知∠A=90°,AB=3,我們是不是可以連線BE, BE和CD相交於點F。
如果可以求出BE的長度,根據勾股定理就可以得到AE的長。
如何去求BE的長呢?
我們看到三角形BCF和三角形EDF。
∠C=∠D=90°,內錯角相等,兩直線平行,BC∥DE。
BC∥DE,兩直線平行,內錯角相等,∠CBF=∠DEF,
所以三角形BCF和三角形EDF是相似的。
假設CF=x,則DF=4-x,
接下來可以透過相似三角形對應邊成比例構造方程,從而求出x,再由勾股定理求出BE的長,這是求BE的一種方法。
除此之外,還有其他的方法嗎?
其實我們可以延長ED,接著過點B作ED延長線的垂線。
如圖BG⊥EG,
四邊形BCDG有三個內角為直角,四邊形BCDG為矩形,
GD=BC=3, BG=CD=4。
在直角三角形BEG中,BG=4,EG=8,由勾股定理可得,BE=√80。
在直角三角形ABE中,AB=3,BE=√80,由勾股定理,可得AE=√71。