複合材料力學 致力於複合材料力學與模擬分析領域知識創作與分享! 591篇原創內容 -->
公眾號
1. 導讀
多孔材料(晶格拓撲材料)作為一種新興材料,它具有優良的力學效能、自由的設計度、易成型等優點。不同的成型技術,如熔模鑄造、焊接、3D列印等是這種週期性晶胞週期材料(晶胞大小從幾毫米到幾十釐米不等)應用最廣泛的製造工藝。然而,這些工藝,尤其是3D列印不可避免地會在材料中誘導產生複雜的微觀結構。此外,不同的微結構又會導致材料表現出不同的力學響應。為了解釋晶格材料複雜的力學行為,眾多的研究者透過將本構關係及其微觀結構聯絡起來,進而研究分析材料的力學響應。
但是,在現有的晶格設計研究中,沒有人考慮過晶格八面體的設計細節,包括改變其晶格的長寬比和相對密度。因此,無法深入分析不同失效模式的發生和材料拓撲之間的關係,這大大限制了對晶格材料在損傷過程和力學響應的研究。
近日,東北大學的Liang Dong(第一作者兼通訊作者),在《Composite Structures》上發表了題為“Mechanical responses of Ti-6Al-4V cuboctahedral truss lattice structures”的文章,在該研究中,作者提出了一個創新的設計方案:首先,設計並製造了具有立方八面體桁架(相當於八面體桁架)拓撲結構的晶格結構材料,隨後,提出採用立方八面體桁架點陣結構來快速裝配鈦合金材料,緊接著,透過真空釺焊的方法對這些材料進行冶金結合,最後,實驗研究了材料壓縮中的力學效能,同時並與有限元和解析預測進行了比較,證明了該猜想的可行性和準確性。
2. 內容簡介
2.1 晶格材料的設計和組裝
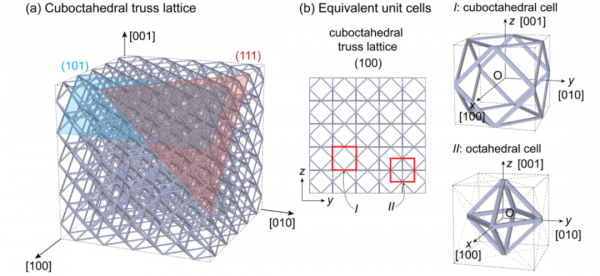
圖1. 結構單元格平移形成的兩種等效銜架晶格:立方體和八面體
圖2. 不同長寬比引數晶胞組裝的立體化桁架結構
2.2 材料的壓縮效能測試
結果表明(圖5):隨著壓縮應變的增加,桁架的節點旋轉和破壞模式由彈性屈曲向非彈性屈曲轉變。在達到晶格峰值強度之前,未檢測到桁架或節點斷裂。載荷的不斷載入導致了平面外桁架單層內的集中變形,直到其中的支柱完全崩潰,這伴隨著應力迅速軟化和應力-應變曲線上幾乎沒有應力的長階段(圖4)。連續載入導致第二層桁架層發生彈性屈曲破壞,應力出現二次峰值;當變形擴充套件到桁架層完全坍塌時,觀察到大量應力軟化的重複發生。
圖3. 三個角度觀察的Ti-6Al-4V立方面體晶格樣品的照片
圖4. 不同相對密度的Ti-6Al-4V立方八面體桁架晶格試樣的壓應力與應變響應;(b)中包含數值預測與實驗測量值的比較
圖5. 不同相對密度的Ti-6Al-4V立方八面體桁架晶格試樣的壓應力與應變響應;(b)中包含數值預測與實驗測量值的比較
圖6. 點陣試樣的壓縮破壞模式照片
2.3 材料壓縮過程中的有限元模擬
利用Abaqus/ Standard軟體(6.13版)的隱式程式碼,研究了預製試件等效的有限元模型(圖7),以及材料的坍塌機理,並檢測了局部應力分佈。透過改杆長徑比t l / 0.068 ~ 0.195,構建了相對密度為1.5% ~ 7.5%的5種有限元模型,有限元模型採用至少6個單元的三維二次四面體單元(Abaqus記數法C3D10)進行網格劃分。值得注意的是,我們進行了更細的網格密度分析,但預測精度的提高卻是微不足道的。圖8中繪製了與實驗測量的應力應變響應相比的等效模型和數值預測應力應變曲線。分別為2.4%和1.5%試樣在不同壓縮應變下的預測變形形態和區域性應力分佈圖(如圖7和圖8所示)。
結果表明,在模擬過程中忽略了基材的斷裂準則,預測的點陣響應與實驗測量資料吻合較好,點陣強度較低。對於密度最低的點陣(ρ= 1.5%),當初始觀察到杆的彈性屈曲變形和節點的旋轉時,應力達到峰值。連續載入導致了平面外桁架單層內的集中變形,表現為支撐屈曲和節點旋轉的發展。在ρ= 1.5%的點陣結構中觀察到最小的平面桁架撓度;我們可在平面外桁架中觀察到最大von Mises應力,而在平面內桁架中觀察不到。
圖7. 有限元預測壓縮變形特性和von Mises應力分佈的等效點陣模型
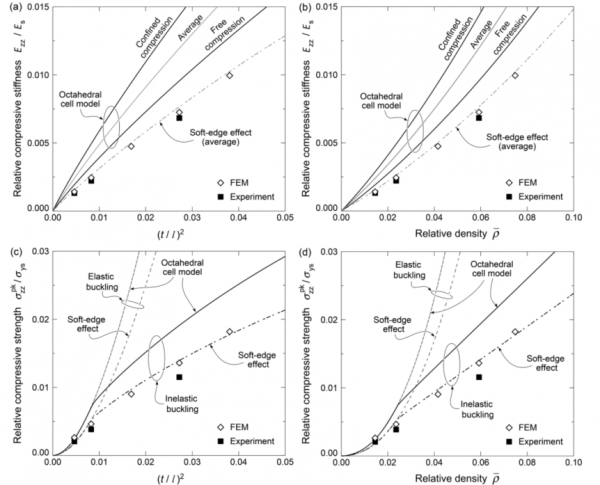
圖8. 比較測量和模型預測的相對彈性模量(a)-(b),強度(c), (d)作為相對密度的函式曲線
2.4 此次設計材料與其他材料的比較
圖9. Ti-6Al-4V立方八面體晶格結構與其他各種胞狀材料的效能比較
3. 小結
作者提出了一個創新的晶格設計成型和裝配方案,並進行了力學實驗和力學模型以及模擬模擬。結果表明:Ti-6Al-4V立方八面體晶格對現有材料和拓撲結構具有競爭性的力學響應;然而,晶格響應與晶格大小有關,只有具有足夠數量的晶格結構中才能實現較高的力學響應。所提出的建模框架可應用於各種由短材料設計體系的分析。
原始文獻:Dong, Liang. "Mechanical Responses of Ti-6al-4v Cuboctahedral Truss Lattice Structures." Composite Structures 235 (2020).