複合材料力學 致力於複合材料力學與模擬分析領域知識創作與分享! 591篇原創內容 -->
導讀
三維機織複合材料由於具有抗衝擊、抗分層、易於設計、加工方便等優點,在各個領域得到了廣泛應用。材料力學效能與織物的結構密切相關,數值模型可以用來研究兩者之間的關係,而建立數值模型的關鍵是能夠準確描述織物結構的幾何形狀。然而,三維機織物的多尺度性質和複雜的內部組織結構增加了建模的難度。為此,天津工業大學的Ziyue Gao(第一作者)和Li Chen(通訊作者)從多尺度的角度綜述了三維機織物的數值分析方法,在《Composite Structures》上發表了題為“A review of multi-scale numerical modeling of three-dimensional woven fabric”的文章,該綜述重點介紹了中尺度和微尺度建模方法的最新進展,討論了纖維間接觸-摩擦相互作用的檢測和建模方法,為三維機織物的模擬研究提供了參考。
內容簡介
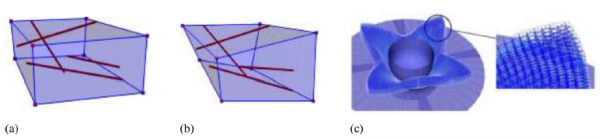
三維機織織物由交錯的紗線組成,紗線中又包含成千上萬的纖維。因此,數值模型的建立必須從織物不同尺度上進行考慮:宏觀尺度(機織物的單元尺度)、中觀尺度(紗線尺度)和微觀尺度(纖維尺度)。在改進模型時應考慮三種剛度(拉伸、平面剪下和彎曲)的影響,特別是彎曲剛度和拉剪耦合的影響。De Luycker等人[33]提出了一種由紗線組成的特殊六面體單元,如圖1所示。這是一種半離散的建模方法,考慮了紗線的分佈,並在次彈性本構中考慮了紗線的特性,將離散的紗線置於連續六面體中可以有效地模擬材料大部分的力學行為,但不能模擬其彎曲變形。
圖1 含纖維紗線的六面體有限元[33](a)初始(b)變形(c)半球成形性
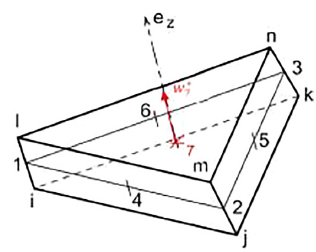
圖2中Xiong[38]提出了基於DKT6板有限元的7節點稜柱體實體殼有限元,其與9節點六面體元相似,在元素中心沿厚度方向增加了平移自由度,進而可以改善厚度行為,作者提出的粘彈性模型可用於模擬纖維增強熱塑性複合材料預浸料的固結行為。
圖2 7節點柱狀固體殼單元[38]
Barbagallo[48]利用二次梯度理論在連續模型的基礎上,考慮了平面剪下變形、不同彎曲剛度和經緯方向的假想伸長,提出了應變能密度的本構表示式。所建立的模型不僅與試驗結果吻合,而且能較好地預測材料變形,模型的效果圖如圖3所示。
圖3 剪下角對第二梯度模型起皺的影響[48]
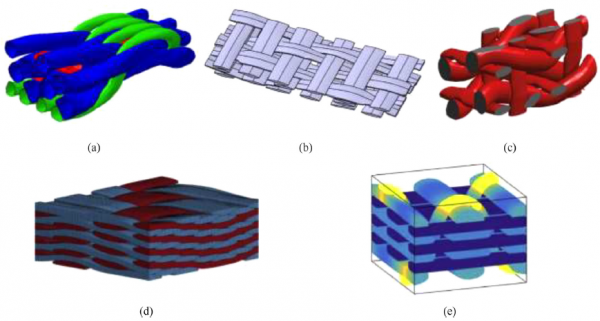
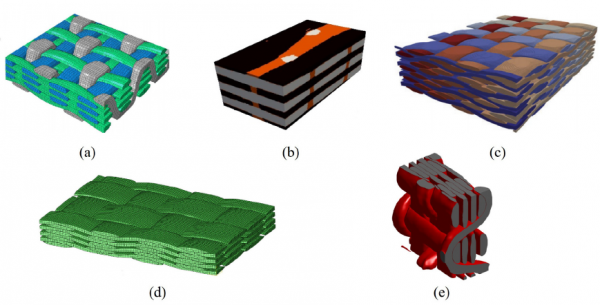
圖4給出了透過物理法對三維織物的細觀幾何模擬結果。圖5給出了三維正交機織織物的三維掃描重建圖,micro-CT裝置的高空間解析度可以對織物內部結構進行詳細掃描,該方法不僅可以重構織物和預浸料中的紗線結構,還可以區分紗線中的纖維[72]。此外,micro-CT的另一個優點是能夠無損地重建材料的內部結構,即掃描過程不會破壞織物的原始結構。圖6進一步給出了不同學者基於micro-CT對三維織物的細觀幾何的模擬結果。然而,基於micro-CT的方法只能對已有的織物進行掃描,缺乏對織物方面的預測能力。同時,影象分析後處理成本高、耗時長,制約了該方法的進一步應用。
圖4 不同的幾何方法對三維織物的細觀幾何模擬結果(a)Stig模型[66](b)Wendling模型[67](c)Wintiba模型[68](d)Nilakantan方法[69](e)Pierreux模型[70]
圖5 三維正交機織織物的三維掃描重建[76]
圖6 利用micro-CT對三維織物的不同重建結果(a)Naouar模型[76](b)Straumit模型[77](c)Huang模型[78](d)Wijaya模型[79](e)Wintiba模型[81]
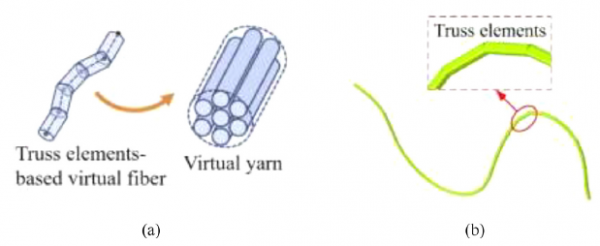
紗線在實際織物中的變形取決於纖維的排列和纖維間的相互作用。纖維在紗線內的相對運動是紗線截面形狀變化的主要原因[82]。因此,必須考慮單個纖維的力學效能,將纖維建為一個“機械元素”,透過彎曲來模擬纖維的相對運動,從而進一步真實地反映織物微觀結構的變化。微觀模型的建立有兩個難點,一是單個纖維的行為模型,二是模擬它們之間的接觸摩擦。目前,建立虛擬光纖模型的方法主要有三種:數字單元法(DEA)、基於桁架元素方法,以及梁單元法。圖7給出了數字單元法的基本概念,其中纖維是具有圓形截面的彈性元素,由一組無摩擦節點組成。當相鄰纖維上的兩個節點之間的距離小於纖維直徑時,在它們之間的接觸面積上添加了接觸元素,接觸面積如圖7(b)所示。
圖7 數字單元法的基本概念(a)虛擬光纖(b)接觸面積[84]
為了提高計算效率,Huang[85]對織物單元提出了一種具有周期邊界的動態鬆弛演算法,如圖8(a)所示。Dobrich[86,87]考慮了織造過程中的紗線引數,如經緯密度、紗線尺寸、紗線捲曲度等,獲得了織物的微觀幾何形狀,模擬結果與實際機織織物非常吻合,如圖8(b)所示。
圖8 基於DEA的不同微觀模型(a)Huang的模型[85](b)Döbrich模型[87]
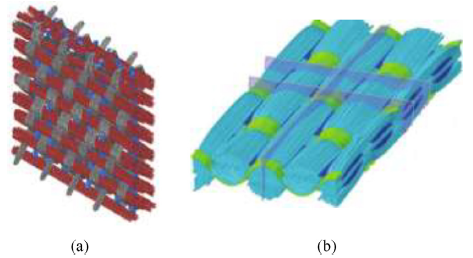
與DEA相似,桁架單元也具有零彎曲剛度的特性,桁架單元的節點視為無摩擦。Daele Inans[91]建立了基於零彎曲剛度桁架結構的虛擬纖維模型,如圖9所示。將織物模型連續壓實,直到達到與實際織物相同的厚度(圖10)。
圖9 桁架單元虛擬纖維圖(a)Daelemans法(b)Ying法
圖10 基於桁架單元的不同微觀模型(a)Daelemans模型[91](b)Ying模型[92]
小結
三維機織物的優異效能促進了學者對其結構設計與最佳化的關注,進而使三維機織織物結構更加複雜多樣。因而新型結構的效能分析已成為研究熱點,而數值模擬方法避免了實際織造過程中大量的人力和物力消耗,能夠模擬任何織物結構,結合有限元分析,極大地促進了三維機織物的發展。其中,紗線細觀幾何建模透過解析幾何和物理方法避免了理想化的紗線形狀,但也造成了紗線間的相互滲透。基於micro-CT影象的建模方法雖然能更好地反映織物內部紗線的實際結構,避免紗線之間的相互滲透,但只能對現有織物進行建模,限制了其應用。對單個纖維進行建模是解決上述問題的一種潛在的方法。
原始文獻:Gao Z, Chen L. A review of multi-scale numerical modeling of three-dimensional woven fabric. Composite Structures 2021, 263:113685..