高效計算和量子力學精確近似求解多電子薛定諤方程,是計算材料科學的關鍵所在。若能夠消除計算成本瓶頸,耦合簇理論等方法,將具有廣泛應用潛力。例如,需要極其密集的K點網格,來模擬長程電子相關效應,特別是對於金屬。儘管在偏移(或扭曲角)上取平均,可以使這些網格更有效,但耦合簇理論coupled cluster theory的最終時間成本,還是令人望而卻步。
近日,美國愛荷華大學James J. Shepherd團隊,聯合維也納工業大學理論物理系,在Nature Computational Science上發文,報道了可以使用過渡結構因子transition structure factor,找到單個特殊扭曲角twist angle,這提供了與扭曲平均twist averaging相同的好處,在計算時間上減少了一個或兩個數量級。研究證明,這不僅適用於金屬系統,而且適用於更廣泛的材料,包括絕緣體和半導體。

A shortcut to the thermodynamic limit for quantum many-body calculations of metals
金屬量子多體計算熱力學極限的捷徑。

圖1:計算效率資料的結構因子扭轉平均structure-factor-based twist averaging sfTA。
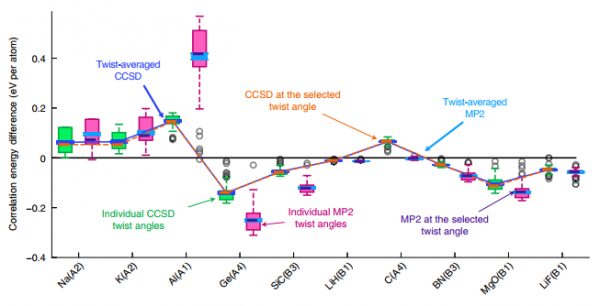
圖2:一系列系統扭轉平均和結構因子扭轉平均structure-factor-based twist averaging sfTA的Γ中心網格能量差。
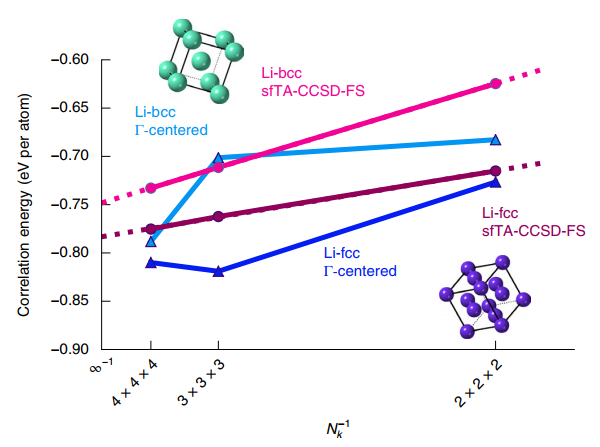
圖3:結構因子扭轉平均structure-factor-based twist averaging sfTA-耦合簇理論單雙粒子coupled cluster theory singles and doubles CCSD-有限尺寸修正finite-size correction FS適用於兩相鋰。

圖4:SFTA-CCSD矽金剛石和β-Sn相的能量-體積曲線。
週期耦合簇理論Periodic coupled cluster theory,相較於量子蒙特卡羅方法,更多受益於選擇扭曲角,主要因為兩個重要原因。一是來自關聯扭曲平均(或平衡)描述的基集basis-set,不完全性誤差更可靠地與電子數交換。這可以大大減少處理小帶隙金屬材料所需的基集尺寸。二是,熱力學極限thermodynamic limit TDL 校正,依賴於相同的關係,並且增加的互換性,也有助於這些校正變得更加一致。總之,K點網格小偏移small offset,意味著在計算機時間方面成本過高的過往計算,現在將成為實現的可能。
文獻連結:https://www.nature.com/articles/s43588-021-00165-1
https://doi.org/10.1038/s43588-021-00165-1
https://www.nature.com/articles/s43588-021-00165-1.pdf