為啥春節搶紅包總不是手氣最佳？看完微信搶紅包演算法你就明白了

PK創意鬧新春，我正在參加「春節創意投稿大賽」，詳情請看：春節創意投稿大賽”

前言

春節必不可少的活動就是搶紅包啦，從以前的紙質紅包到現在網際網路紅包（以微信紅包為首），今天我們就來分析一下搶紅包的演算法，其中有一些是微信紅包的演算法，看完你就知道手氣最佳是如何產生的啦！

演算法一：剩餘金額隨機法

演算法一是不推薦使用的，演算法一全稱叫剩餘金額隨機法，聽名字就知道這個方法是將剩餘的金額進行隨機分配，我們先來看程式碼。

// 分配紅包的演算法
private static void testPocket(BigDecimal amount, BigDecimal min, BigDecimal num) {
BigDecimal remain = amount.subtract(min.multiply(num));
final Random random = new Random();
final BigDecimal hundred = new BigDecimal("100");
BigDecimal sum = BigDecimal.ZERO;
BigDecimal redpeck ;
for (int i = 0; i < num.intValue(); i++) {
    final int nextInt = random.nextInt(100);
    if (i == num.intValue() - 1) {
        redpeck = remain;
    } else {
        redpeck = new BigDecimal(nextInt).multiply(remain).divide(hundred, 2, RoundingMode.FLOOR);
    }
    if (remain.compareTo(redpeck) > 0) {
        remain = remain.subtract(redpeck);
    } else {
        remain = BigDecimal.ZERO;
    }
    sum = sum.add(min.add(redpeck));
    System.out.println("第" + (i + 1) + "個人搶到紅包金額為：" + min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP));
}
System.out.println("紅包總額：" + sum.setScale(2, BigDecimal.ROUND_HALF_UP));
}
// 測試程式碼
public static void main(String[] args) {
    BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP);
    testPocket2(amount,min,num);
}
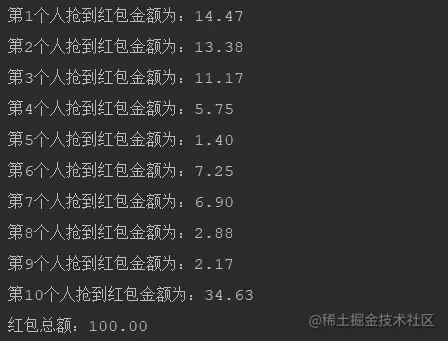
複製程式碼

我們可以看到，這個方法是有很明顯的缺陷的，就是一開始領到紅包的人獲取的金額可能是最大的，後面領取的金額就逐漸變小了，因為他是從剩餘額金額進行隨機的。很顯然微信是肯定不會使用這種方法作為紅包瓜分演算法，不然每次一有紅包，馬上領取就有可能獲取手氣最佳，但是明顯不是。

演算法二：整體隨機法

整體金額隨機法的公式：紅包總額 * 隨機數/隨機數總和，這個方法的核心是使用一個隨機數作為紅包瓜分的標準，這個隨機數是透過Random類隨機產生的。他的隨機性就比較大了，看起來好像是和我們平時搶紅包差不多，但是微信紅包也不是採用這種方法，因為這種的隨機性太大了，不是很公平。


private static void testPocket2(BigDecimal amount,BigDecimal min ,BigDecimal num){
    final Random random = new Random();
    final int[] rand = new int[num.intValue()];
    BigDecimal sum1 = BigDecimal.ZERO;
    BigDecimal redpeck ;
    int sum = 0;
    for (int i = 0; i < num.intValue(); i++) {
        rand[i] = random.nextInt(100);
        sum += rand[i];
    }
    final BigDecimal bigDecimal = new BigDecimal(sum);
    BigDecimal remain = amount.subtract(min.multiply(num));
    for (int i = 0; i < rand.length; i++) {
        if(i == num.intValue() -1){
            redpeck = remain;
        }else{
            redpeck = remain.multiply(new BigDecimal(rand[i])).divide(bigDecimal,2,RoundingMode.FLOOR);
        }
        if(remain.compareTo(redpeck) > 0){
            remain = remain.subtract(redpeck);
        }else{
            remain = BigDecimal.ZERO;
        }
        sum1= sum1.add(min.add(redpeck)).setScale(2, BigDecimal.ROUND_HALF_UP);
        System.out.println("第"+(i+1)+"個人搶到紅包金額為："+min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP));
    }

    System.out.println("紅包總額："+sum1);
}

// 測試程式碼
public static void main(String[] args) {
    BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP);
    testPocket2(amount,min,num);
}

複製程式碼

他的隨機性可謂是很高，也不是最佳選擇。

演算法三：割線法

割線法指的是把紅包總金額想象成一條很長的線段，而每個人搶到的金額，則是這條主線段所拆分出的若干子線段，當所有切割點確定以後，子線段的長度也隨之確定。這樣每個人來搶紅包的時候，只需要順次領取與子線段長度等價的紅包金額即可。

private static void testPocket3(BigDecimal amount, BigDecimal min, BigDecimal num) {
    final Random random = new Random();
    final int[] rand = new int[num.intValue()];
    BigDecimal sum1 = BigDecimal.ZERO;
    BigDecimal redpeck;
    int sum = 0;
    for (int i = 0; i < num.intValue(); i++) {
        rand[i] = random.nextInt(100);
        sum += rand[i];
    }
    final BigDecimal bigDecimal = new BigDecimal(sum);
    BigDecimal remain = amount.subtract(min.multiply(num));
    for (int i = 0; i < rand.length; i++) {
        if (i == num.intValue() - 1) {
            redpeck = remain;
        } else {
            redpeck = remain.multiply(new BigDecimal(rand[i]))
                .divide(bigDecimal, 2, RoundingMode.FLOOR);
        }
        if (remain.compareTo(redpeck) > 0) {
            remain = remain.subtract(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP);
        } else {
            remain = BigDecimal.ZERO;
        }
        sum1 = sum1.add(min.add(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP));
        System.out.println("第" + (i + 1) + "個人搶到紅包金額為：" + min.add(redpeck));
    }

    System.out.println("紅包總額：" + sum1);
}
// 測試程式碼
public static void main(String[] args) {
    BigDecimal amount = new BigDecimal(100).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal min = new BigDecimal(0.01).setScale(2, BigDecimal.ROUND_HALF_UP);
    BigDecimal num = new BigDecimal(10).setScale(2, BigDecimal.ROUND_HALF_UP);
    testPocket2(amount,min,num);
}
複製程式碼

他的隨機性也比較大，但是他最致命的是效能，因為他需要進行切割這個步驟。

演算法四：二倍均值法

演算法四就是微信紅包目前所採用的的演算法（大致思路，程式碼模擬），二倍均值計算公式：2 * 剩餘金額/剩餘紅包數。

  BigDecimal remain = amount.subtract(min.multiply(num));
    final Random random = new Random();
    final BigDecimal hundred = new BigDecimal("100");
    final BigDecimal two = new BigDecimal("2");
    BigDecimal sum = BigDecimal.ZERO;
    BigDecimal redpeck;
    for (int i = 0; i < num.intValue(); i++) {
        final int nextInt = random.nextInt(100);
        if(i == num.intValue() -1){
            redpeck = remain;
        }else{
            redpeck = new BigDecimal(nextInt).multiply(remain.multiply(two).divide(num.subtract(new BigDecimal(i)),2,RoundingMode.CEILING)).divide(hundred,2, RoundingMode.FLOOR);
        }
        if(remain.compareTo(redpeck) > 0){
            remain = remain.subtract(redpeck).setScale(2, BigDecimal.ROUND_HALF_UP);
        }else{
            remain = BigDecimal.ZERO;
        }
        sum = sum.add(min.add(redpeck)).setScale(2, BigDecimal.ROUND_HALF_UP);
        System.out.println("第"+(i+1)+"個人搶到紅包金額為："+min.add(redpeck));
    }
    System.out.println("紅包總額：" + sum);
}
複製程式碼