來源:騰訊量子實驗室
01背景介紹
絕熱演化是一種在經典和量子系統中均有廣泛應用的控制策略。 在經典情境下,顧名思義,系統與環境不發生熱量交換。而在量子體系中,系統將不會在瞬時本徵態之間發生躍遷。 絕熱演化過程可以作為一種演算法方案完成需要的資訊處理任務。然而,絕熱過程通常要求很慢的演化速度。由於當今量子技術中位元壽命有限,這給緩慢絕熱過程的應用帶來很大的侷限性。為了克服這一速度限制,人們發展了各種加速絕熱演化的實驗方案。這些控制策略使得系統在極短的時間內實現目標絕熱演化,而不引起遠離瞬時平衡狀態的不好結果。

圖1. 絕熱捷徑效果示意圖。絕熱捷徑控制方案可以加速傳統上必須緩慢變化的絕熱演化。
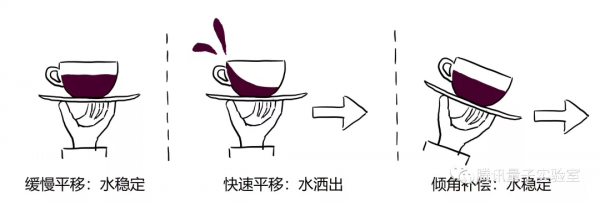
實際上在日常生活中,人們經常不自覺地使用這一策略。如圖2所示,當我們需要快速移動一個盛滿水的杯子但又不想讓杯中的水撒出時,就會不自覺地改變手持杯子的姿勢來彌補快速移動造成的脫離平衡態的趨勢。此外,賽車手進行漂移過彎時,車輛實際路徑和方向盤控制的方向也有很大差異。這正是賽車手利用控制上的偏離彌補了轉彎時的巨大離心力,才可以實現快速轉彎,而不衝出賽道。由此可見,這一控制策略在經典場景是極其常見的。
那麼,類似的控制策略是否也可以被應用到量子系統呢? 答案是肯定的。事實上,早在近20年前,類似的思想已經被應用在量子調控上了。後來隨著量子資訊科學的蓬勃發展,人們對量子態精確調控與複雜演化控制的需求越來越高,量子絕熱捷徑得到了越來越多的關注【1】。
反向透熱補償(counterdiabatic, CD)是量子絕熱捷徑中一類常用的方法。在移動水杯的例子中,我們透過傾斜杯子,使得一部分的重力抵消了加速過程中使水溢位的慣性力。在量子系統中,類似的,當我們快速改變一個系統的哈密頓量時,也會產生一個“慣性哈密頓量”從而導致不同能級間的躍遷。因此,我們可以額外施加一個相反的哈密頓量來抵消導致躍遷的效果,從而使系統一直處在固定的能級之上來實現絕熱捷徑,這便是反向透熱補償的基本原理。
第一個基於反向透熱補償方法的量子絕熱捷徑首先在離子阱系統中被驗證【2】。透過使用輔助驅動,人們可以使離子的任意運動狀態始終處在瞬時基態上,從而實現在遠遠小於一個離子振動本徵振動週期內的遠距離無激發移動。
在量子相關的實驗中,由於受環境中擾動的影響,絕大部分系統實際上是開放量子系統(open quantum systems),不再嚴格遵守薛定諤方程,而會經歷額外的、不可逆的耗散過程。因此,對於開放量子系統的控制是量子調控領域一個很重要的問題。雖然適用於開放量子系統的絕熱演化絕境在理論上已經被提出【3】,甚至適用於介觀開放系統的絕熱捷徑也被驗證【4】,但真正適用於微觀開放量子體系的絕熱捷徑尚未被設計和證實。
在本研究中,作者利用與環境耦合的超導腔QED系統,首次驗證了開放量子系統的絕熱捷徑。目前大量的經典/量子混合演算法和糾錯都需要電路的途中測量。由於超導位元的讀取需要對讀取諧振腔進行激發,而位元的操作會受到讀取腔殘留光子影響,故每次讀取完畢後都要等待較長時間來清空讀取腔中的光子。為加快途中測量,減少不必要等待,作者把加速量子開放系統絕熱演化的理論應用到超導位元的讀取加速,實現了在一個衰減常數內,讀取腔6-8倍的加速激發和清零。該工作為更廣泛的量子絕熱捷徑技術的應用鋪平了道路。
02實驗過程
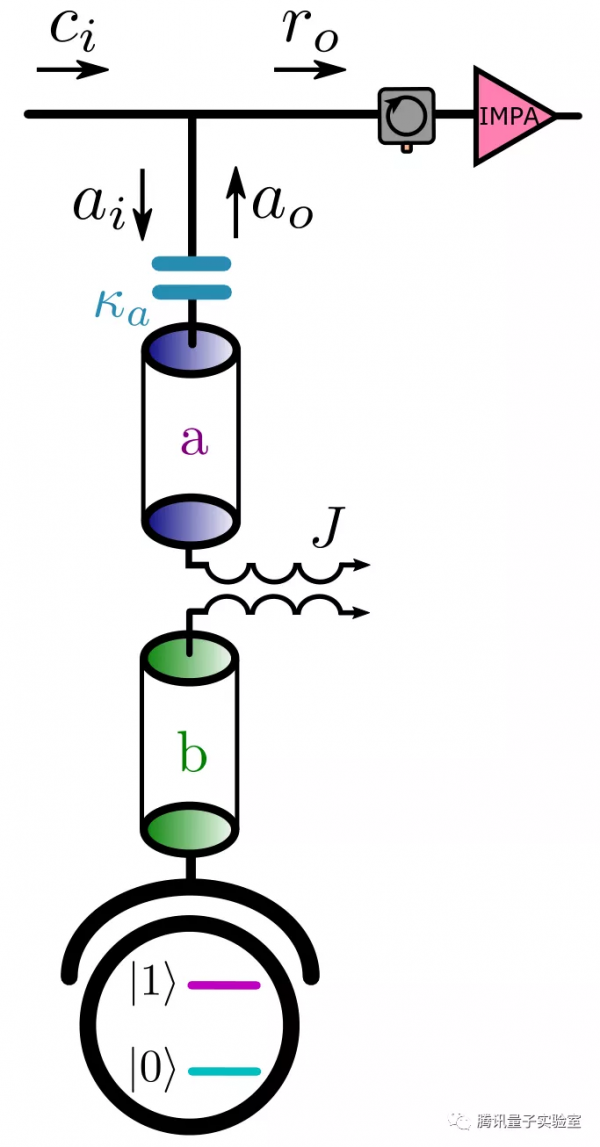
本研究利用的系統包含一個transmon超導位元,兩個級聯耦合的諧振腔(a模式和b模式),和與環境相連的讀取線。研究者可以用位元的0,1狀態控制直接相連的b模式的頻率。a模式與b模式透過相互作用J耦合雜化到一起。整個系統又透過Ka代表的電容耦合與代表環境的讀取線耦合。實驗者可以透過施加外部驅動ci來改變整體系統的狀態。系統的狀態則可以從其洩露的微波ro經過層層放大之後得到。
如果透過ci施加的控制就是一個正常的sin²形的上升沿脈衝。那麼可以透過不斷提高上升沿的時間來最終實現無瞬時激發的絕熱演化。從圖4a,b的結果看,在本實驗的引數範圍內,需要大約800ns(紫色),才能使得系統響應基本跟隨控制波形。如果縮短到100ns(紅色),在初始的300ns內,系統都會出現震盪(圖4b),與施加的控制波形偏離。但是當作者按照開放系統絕熱捷徑的理論施加對應的補償波形時(橙色),系統演化會在100ns左右達到平衡(圖4b)。從而在實驗上首次驗證了可以快速地到達量子系統平衡態。進一步,在圖4c中,可以利用輸入輸出理論得到系統的相空間演化軌跡。在施加反向透熱補償控制時,在100ns系統已經基本到達平衡態。但如果不加,在圖4d中100ns時的軌跡還是遠離最終平衡態的。
(a) 不同上升沿的漸變波形與反向透熱補償控制波形對比。 (b) 與控制波形對應的系統洩露輸出的強度。系統的演化狀態可以從之推出。(c), (d) 為(b)中同一過程在相空間中的演化。原點用十字表示。平衡態為除了原點外另一高密度軌跡中心。可以看出,在100ns的時候(綠色點),使用CD(圖c)已經基本達到平衡態,但是不使用CD(圖d)還遠未達到平衡態。
截至這裡,作者已經成功設計並驗證了一個基於開放系統絕熱捷徑的實驗方案。但是,為了使本技術更加實用化,比如應用於超導位元讀取等多頻場景,作者還利用最佳化控制的理論開發了相容多個模式的絕熱捷徑,即用一個脈衝波形快速達到多個模式的快速平衡。
這一方法的基本思想為假設脈衝波形具有分段方波的形式(如圖5a所示),透過使分段數量(自由度)大於系統平衡需要滿足的約束數量,可以求出波形的解析解。這裡的約束為使每個目標模式在目標時間達到讀取平衡態。值得注意的是,由於位元的狀態會改變b模式的頻率從而影響a,b模式中各自對應的簡正模式(或混合模式),因此將位元每個狀態下的每個模式視作不同的、互相獨立的模式。在實驗中,有2個位元狀態和2個模式,於是有4個需要平衡的獨立模式,即4個約束。作者選擇了長度為60ns,總計分為10段的分段方波,使得系統的總自由度數量為10,大於約束數量。透過基於input-output理論的計算,可以將約束轉化為以每段脈衝的復振幅為變數的線性方程組,並利用奇異值分解的方法得到波形的通解。通解中冗餘的自由度可以進一步最佳化以實現多種目的。
比如這裡作者把最佳化目標設為減小最大脈衝強度。由此減小對系統的過度激發,避免不必要的高階非線性過程。最佳化之後的脈衝波形見圖5a。如果把這一多模最佳化控制波形應用到撤去激發的過程,則可以實現不依賴位元狀態的快速超導位元讀取腔的重置。對比結果如圖5b,c在1000ns時所示。
控制波形如(a)所示。從(b), (c)中在1000ns時,絕熱捷徑驅動結果與一般直接撤去激發的對比可知:無論位元處在0或1態,多模最佳化控制的快速reset機制都可以使系統很快穩定到平衡態。從而實現了讀取腔的無條件重置。
在本研究的最後,作者還展示了對實驗系統的過強驅動,會導致劇烈的非線性過程和位元的激發(見圖6),展示了在非線性系統中本捷徑方法實現更快平衡過程時遇到的侷限,也為進一步研究指明瞭一個方向。

圖6. 系統驅動強度超過某一臨界值時,位元會突然發生劇烈激發,即相變行為,導致絕熱捷徑失效。
03意義和展望
作者在實驗上首次驗證了開放系統的量子絕熱捷徑,為這一技術的應用打開了更廣闊的的空間。同時,為了應用於更復雜的多模情況,作者也基於最佳化控制理論開發了多模最佳化控制,實現了快速無條件達到體系平衡態。該方案可以應用於加速超導位元讀取和讀取之後諧振腔的快速初始化,從而加速途中測量。同時,這裡的方案也可以用於加速複雜驅動耗散穩態(比如貓態)的製備,也可以用於加快光力系統的冷卻。如果把理論中的耗散設定為0,就立即回到了封閉量子系統的情形。這裡的方案也就可以應用於匯流排介導的全域性門控制方案【5】。值得注意的是,最近也有理論指出,開放系統絕熱捷徑也可應用於生物物理【6】等跨學科場景。
參考文獻:
[1] Gu´ery-Odelin, D. et al. Shortcuts to adiabaticity: Concepts, methods, and applications. Reviews of Modern Physics 91, 045001 (2019).
[2] An, S., Lv, D., Del Campo, A. & Kim, K. Shortcuts to adiabaticity by counterdiabatic driving for trapped-ion displacement in phase space. Nature communications 7, 1–5 (2016).
[3] Vacanti, G. et al. Transitionless quantum driving in open quantum systems. New Journal of Physics 16, 053017 (2014)。
[4] Mart´ınez, I. A., Petrosyan, A., Gu´ery-Odelin, D., Trizac, E. & Ciliberto, S. Engineered swift equilibration of a brownian particle. Nature physics 12, 843–846 (2016).
[5] Cai, T.-Q. et al. All-microwave nonadiabatic multiqubit geometric phase gate for superconducting qubits. Physical Review Research 3, 043071 (2021).
[6] Iram, S. et al. Controlling the speed and trajectory of evolution with counterdiabatic driving. Nature Physics 17, 135–142 (2021).