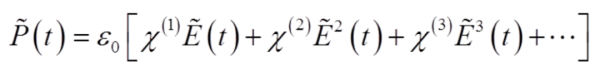提起這個月的工作重點,
相信大家都會不約而同的說出——
坐等過年!
實不相瞞,
最近小編在實驗室…
擰著螺絲想過年,
做著測試想過年,
改著草稿想過年…
雖然距離過年還有一段時間,
但烘托過年氛圍的物件已經可以開始準備起來了!
寒冷的冬天,
在表面微微結霜的窗戶上貼上精緻有趣的窗花,
是小編過年最喜歡的活動之一啦!
古老的民間藝術——窗花
貼在窗戶上蘊含著滿滿年味兒的窗花,承載了上千年的農耕文化,從宋朝、元朝逐漸流傳,逐漸成形。
在明清時期,剪紙手工藝術達到了鼎盛時期。清代也有著“剪畫聰明勝剪書,飛翔花鳥泳瀕魚。任他二月春風好,剪出垂楊恐不如。”這樣的詩句來描繪剪紙藝術。
時至今日,窗花依然寄託著大家的美好願望,將節日裝點得紅火富麗、喜氣洋洋。
對於剪紙藝術,你知道有哪些技法嗎?
剪紙是一種鏤空連線的藝術品,按照鏤空形式可以分為陰剪(刻)、陽剪(刻)兩大類。
陰剪是將圖形從紙上剔除,具有“線線相斷”的特點;而陽剪是將圖形保留,具有“線線相連”的特點。
陰剪和陽剪示意圖 | 圖片來源:剪紙大圖譜
這技法…好像腦子懂了,手卻沒懂…
很多圖案具有對稱性的剪紙作品都是透過折剪的方法得到的——將紙張由於紙張以各種不同方式摺疊為多層,在摺好的紙上進行剪鏤。
透過這樣的方法,會在折縫上留下連線點,開啟來就是一張具有對稱性的剪紙作品。
簡單的折剪 | 圖片來源:剪紙大圖譜
除了技法之外,剪紙作品的圖案內容也是非常豐富多彩的,通常是吉祥題材剪紙,多為花卉植物、動物飛禽、瓜果蟲魚、山水風景、人物題材和勞動題材。
春耕/膠南剪紙/民間剪紙藝人劉學芳作 | 圖片來源:中國鄉村剪紙經典
漁業豐收/樂清細紋刻紙 | 圖片來源:中國鄉村剪紙經典
花籃花兒香/老剪紙 | 圖片來源:中國鄉村剪紙經典
除此之外,生肖也是剪紙作品的重要題材之一,為了迎接即將到來的虎年,我們一起來看看精美的虎剪紙吧~
虎生肖/老剪紙 | 圖片來源:中國生肖剪紙經典
上面這些剪紙作品是不是很生動活潑、精美絕倫?雖然小編不會做剪紙,但我們可以一起從剪紙裡挖一挖物理知識。
變了又沒變——對稱性
對稱性是指一個圖案能夠在經過一種變換操作後能夠和原來的圖案重合的性質。
我們一起來看看具有對稱性的剪紙作品:
圖片來源
圖片來源
仔細看看這些圖案,我們會很容易的聯想到幾何對稱——軸對稱、旋轉對稱、映象對稱等等。
我們可以將對稱分為:反射對稱(reflective symmetry)、旋轉對稱(rotational symmetry)、平移對稱(translational symmetry)。除此之外,還有瑕旋轉(Improper Rotation)、滑移反射(Glide Reflection)、螺旋旋轉(Screw Rotation)這類在兩種變換同時進行的條件下保持不變的對稱性。
(關於對稱型別的詳細介紹可以檢視往期內容:什麼是對稱?)
提到物理學中的對稱性,最容易想到的就是——晶體。晶體同時具有宏觀對稱性和微觀對稱性:宏觀對稱性就是點對稱性,表現在晶體的幾何外形上,同時反映在晶體的宏觀物理性質中;而微觀對稱性除了所有宏觀對稱操作以外,還多了平移對稱性,以及由平移和旋轉,反映組合成的新對稱元素。
(更多有關晶體對稱性的知識可以檢視往期內容:哈!原來古老的窗花中蘊含著這樣的規律?)
對稱性不僅是視覺上的,實際上它是內涵更廣的概念,可以理解為“變換下的不變性”。將對稱性的思想進一步推廣,我們可以看到物理定律中蘊含的對稱性。在物理學中,一些基礎研究都與某些保持不變的物理量或者模式相關。
當我們處於正在運動的列車中,只要列車不進行加速、減速、轉彎等活動,列車裡的情況給我們的感受與我們在地面是相同的。這之中所蘊含的知識是:兩個慣性參考系中的物理規律完全相同,是一種重要的對稱性。
諾特定理指出——物理學裡的連續對稱性和守恆定律一一對應。
質能守恆對應時間平移不變性;動量守恆對應空間平移不變性;角動量守恆對應於旋轉不變性。
藝術美、晶體、物理定律等等都在向我們說明著對稱性之美,然而,當對稱性被打破,我們會得到更加深刻有趣的結果。
對稱性破缺與二次諧波
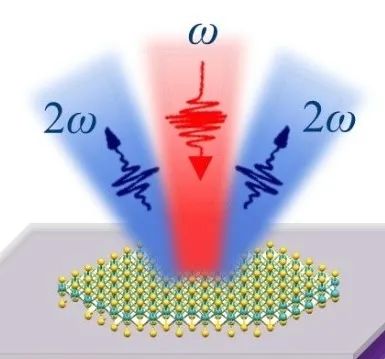
從光學的角度來看,二次諧波(SHG)就是一種與對稱性破缺高度相關的現象。
二次諧波是一種二階非線性光學現象,屬於和頻非線性效應中的一種。
兩個相同頻率光子與非線性材料相互作用後合併成一個兩倍頻率的新光子。
二次諧波示意圖 | 圖片來源[5]
在應用方面,SHG成像技術被廣泛應用於材料科學、多相催化、介面物理化學及生物醫學等。
我們在什麼情況下才能獲得二次諧波呢?
與其他偶數階非線性光學現象一樣,一般我們在具有非中心對稱性的化學結構才可以觀測到SHG現象。
非線性光學現象廣泛的存在於各種不同的介質中,當光場E作用於介質,會產生介質極化強度P。
其中,第一項表示線性極化,第二項則對應著二階非線性光學效應。
在具有中心對稱性質的介質中,二階極化強度之和為零,因此不具有二階非線性極化。這是對稱性破缺在非線性光學領域的一個典型例子。
聲波與對稱性破缺
除了光與物質相互作用之外,將對稱性破缺引入聲波也可以帶來令人感到驚喜的效果。
倫敦聖保羅大教堂的建築內有一個奇特的去處——耳語廊,你可以和朋友坐在兩面遙遙相對的牆壁旁,對著牆壁悄聲對話,雖然看不見對方,卻能與對方交流。
圖片來源
“耳語廊”模式也被稱為“迴音壁”模式,由於聲波沿著迴廊光滑的牆內壁連續反射來進行傳播,因而傳播損耗很小,這也是對稱性在日常生活中很有趣的現象。
基於這種有趣的效應,湧現了大量的研究成果,我們可以透過在器件中人為製造“迴音壁”結構,實現聲波甚至光波的定向傳導。
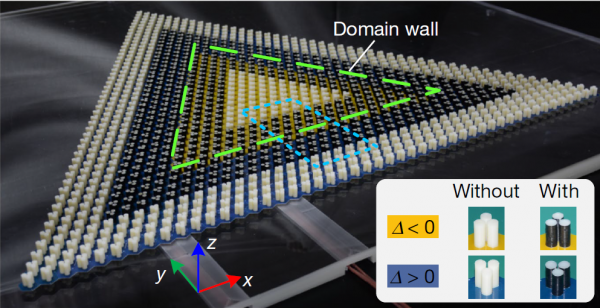
一種人造的“迴音壁”結構 | 圖片來源[8]
在人造的“迴音壁”結構中,可以新增不同的元素來打破聲波的對稱性:透過打破手性對稱性增加增益,允許有選擇地放大聲波;或者增加拓撲這樣的幾何佈置,打破旋轉對稱性,允許聲波在所需的方向上迴圈。
這種結構透過引入對稱性破缺實現了對聲波強度和方向的調控,也具有廣泛的應用前景。
對稱性破缺與相變
在凝聚態物理領域,朗道將相變與物質結構中對稱性的變化相聯絡。
相變是指物質從一種相轉變為另一種相的過程。一級相變是指在發生相變時,物質同時出現體積的變化和熱量的吸收或釋放。
朗道將從高對稱到低對稱的相變過程成為“對稱破缺”。
另外一個重要的概念是“序參量”,用於反映晶體結構或者電子結構的有序程度。
可能與我們的直覺相反,“對稱性”和“有序性”兩者是相反的關係。越有序的結構,對稱性反而越低。
以水為例,氣態水、液態水和冰分別對應水的氣、液、固三態,水在這三種狀態之間的轉變就是相變過程。
冰 | 圖片來源:pixabay
水 | 圖片來源:pixabay
從對稱性來考慮,液相水分子呈無序排列,在每個水分子周圍距離相同的位置上,其他原子佔據的機率是相同的,因此具有較高的對稱性;而固相水分子嚴格按照週期性排列,其他原子位於某一原子周圍的機率是各向異性的,因此相較於液相在結構上對稱性較低。
而從有序性來考慮,液態中的水分子做著隨機而無規則的布朗運動(Brownian Motion)——沒有固定的方向,沒有固定的位置,處於完全無序的狀態,在任何方向、任何點看起來都是一樣的,因此有序性較低;固態中水分子的排列很規則,有序性較高。
根據朗道的理論,從液態水到冰的相變過程就是“對稱破缺”而有序性提高的過程。
在發生相變時,體積不變化的情況下,也不伴隨熱量的吸收和釋放,只是熱容量、熱膨脹係數和等溫壓縮係數等的物理量發生變化,這一類變化稱為二級相變。例如鐵磁順磁相變、零磁場下金屬超導態和正常態的轉變等。
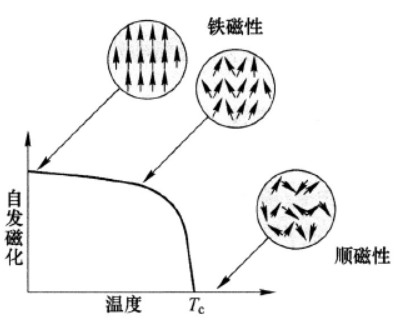
以鐵為例,鐵原子具有磁矩,當磁矩排列趨於相同的方向,表現為鐵磁性。當我們將溫度升高,鐵磁性會發生變化,磁矩的方向開始失去規律。當溫度升高到某一臨界值時,磁矩的排列完全失去了同向性,就全亂了,表現為順磁性,這一臨界溫度也被稱為居里溫度。
鐵磁順磁相變 | 圖片來源
因此,從順磁到鐵磁的相變過程對應著對稱性破缺,有序性提升。
朗道相變理論使我們對於各種各樣物質狀態之間轉變的研究更為簡潔高效,是凝聚態物理領域重要的基礎理論。
兩種對稱性破缺
對稱破缺可以分為:明顯對稱性破缺(Explicit Symmetry Breaking)和自發對稱性破缺(Spontaneous Symmetry Breaking)。
明顯性對稱破缺源於自然規律,是指對於一些物理系統中不具有物理規律的對稱性。
而自發對稱性破缺是指物理系統所遵守的自然定律具有某種對稱性,而物理系統本身並不具有這種對稱性,是一種自發性過程。
如下圖所示,假設在墨西哥帽的帽頂有一個圓球,其將處於旋轉對稱性狀態,即圍繞帽子中心軸的旋轉,圓球的位置不變。
但這種狀態是極不穩定的,引入輕微的擾動就會導致圓球掉落——這時帽子仍然具有旋轉對稱性,而掉落的圓球則導致旋轉對稱性被打破。
儘管這圓球在帽子谷底的所有可能位置因旋轉對稱性而相互關聯,但實際上,圓球在谷底的位置不具有旋轉對稱性。這就是一個比較容易理解的自發對稱性破缺的例子。
圖片來源
我們比較熟悉的BCS理論和希格斯機制都是典型的自發性對稱性破缺的例子。更進一步,電磁力和弱相互作用的統一和基本粒子的質量起源問題也由此被解決。
對稱性破缺與宇稱不守恆
在物理學中,楊振寧、李政道先生在1956年提出的宇稱不守恆就與上面提到的明顯性對稱性破缺相關。
宇稱是描述粒子在空間反演下變換性質的相乘性量子數,記為P,只有+1和-1兩個值。如果描述某一粒子的波函式在空間反演變換(r→-r)下改變符號,該粒子具有奇宇稱(P=-1),如果波函式在空間反演下保持不變,該粒子具有偶宇稱(P=+1)。
宇稱不守恆定律,是指在弱相互作用中,互為映象的物質的運動不對稱。
在1956年以前,θ-τ這兩種質量和壽命幾乎相同,而衰變模式不同的粒子困擾著當時的物理學家們。楊振寧、李政道先生跳出了對稱性的思維,轉而思考另一種可能性:在弱相互作用中,宇稱不守恆。
不久之後,吳健雄先生觀測低溫下鈷60的衰變,為弱相互作用中的宇稱不守恆提供了實驗證據。
這也是物理學家們在探索自然過程中對稱性破缺的思想起到了重要引導作用的著名例子。
讀到這裡,你還記得我們是怎樣一路從窗花講到這麼多的物理知識嗎?
有時我們直觀感受到很簡單的知識和現象,反而能將我們帶領到深刻的學術理論中。
對稱性破缺的引入確實給我們帶來了很有趣且深刻的物理學理論和現象。
那麼現在…複雜精美的窗花和深奧優美的物理學知識你掌握了哪個呢?
小編依然感覺…
參考文獻:
[1]《剪紙大圖譜》
[2]《中國鄉村剪紙經典》
[3]《中國生肖剪紙經典》
[4]《中國風·剪紙入門》
[5] https://zhuanlan.zhihu.com/p/165078880
[6]《非線性光學物理》
[7]郭雅文,李源,馬宗偉.基於二次諧波產生技術的BaTiO_3薄膜對稱性研究[J].光學學報,2021,41(06):191-196.
[8]BolunHu et al, Non-Hermitian topological whispering gallery, Nature (2021).
[9] L.D.Landau,On the theory of phase transitions,1937.
[10]《相變和臨界現象》
[11] Nambu,Y.; Jona-Lasinio, G. (April 1961). "DynamicalModel of Elementary ParticlesBased on an Analogy with Superconductivity.I". Physical Review 122:345–358.
[12]宇稱不守恆 – 百度
編輯:Norma