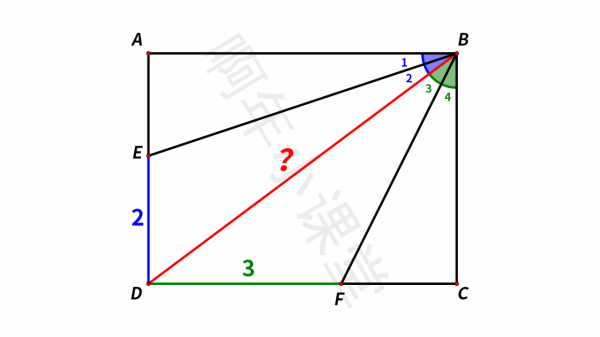
如圖,在矩形ABCD中,∠1=∠2,∠3=∠4,DE=2,DF=3,求BD長。這題怎麼做呢?
∠1=∠2,∠3=∠4,也就是說BE、BF都是角平分線,角平分線有這樣一個性質,角平分線上的點到角兩邊的距離相等。
我們是不是可以分別過點E和點F作BD的垂線?
但是作出這兩條輔助線對求BD的長度並沒有太大的幫助,那麼應該怎麼做呢?
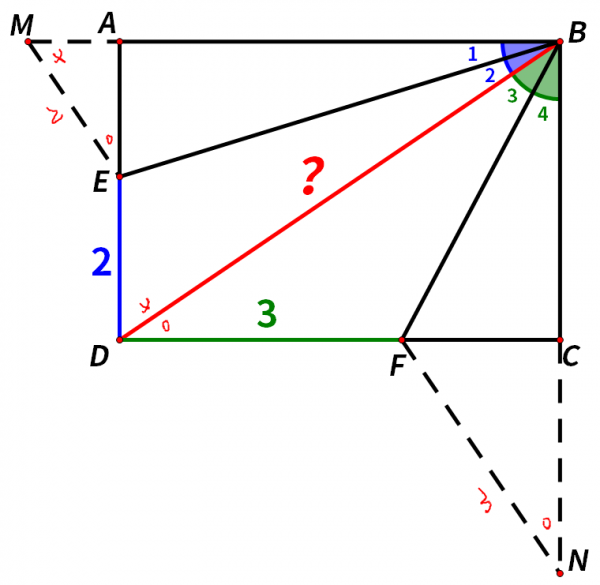
我們可以延長BA以及BC,使得BM=BD,BN=BD,接著再連線ME、NF。
如上圖,由邊角邊證全等可得
三角形BME和三角形BDE全等(BM=BD,∠1=∠2,BE=BE),
三角形BNF和三角形BDF全等(BN=BD,∠3=∠4,BF=BF)。
三角形BME和三角形BDE全等,所以ME=DE=2,∠M=∠ADB。
三角形BNF和三角形BDF全等,所以NF=DF=3,∠N=∠BDC。
而由四邊形ABCD是矩形,可得∠ADB+∠BDC=90°,
而由等量代換可得∠M+∠BDC=90°。
在直角三角形AME中,∠M+∠AEM=90°,等量代換可得∠AEM=∠BDC,
而∠N=∠BDC,所以∠N=∠AEM。
在三角形AEM和三角形CNF中,
∠MAE=∠FCN=90°,∠AEM=∠N,
所以三角形AEM和三角形CNF相似。
三角形AEM和三角形CNF相似,它們的對應邊成比例,
MA/FC=AE/CN=ME/FN,
而ME=2,FN=3,
所以MA/FC=AE/CN=2/3,
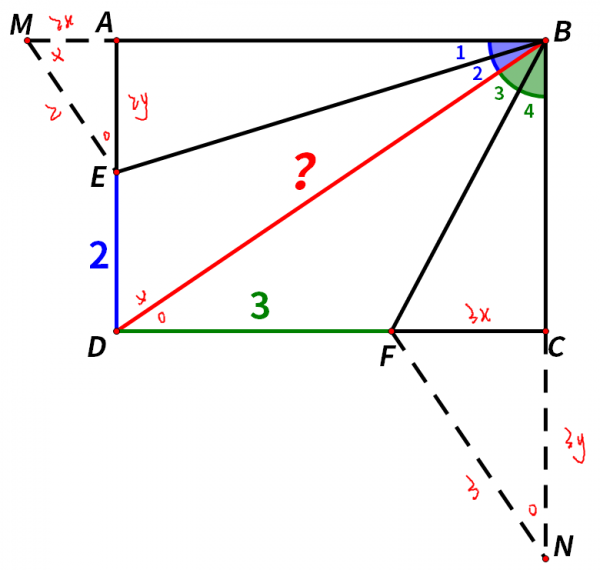
不妨假設MA=2x,AE=2y,則FC=3x,CN=3y,
由勾股定理可得MA²+AE²=ME²,也就是4x²+4y²=4,即x²+y²=1。
而由BM=BD,BN=BD可得BM=BN,
BM=BA+AM=CF+FD+AM=5x+3,
BN=BC+CN=AE+ED+CN=5y+2,
所以5x+3=5y+2。
由x²+y²=1,5x+3=5y+2,解得x=3/5,y=4/5。
BD=BM=5x+3=6。
以上就是這道題的解法。除此之外,你還有其他方法嗎?歡迎在評論區留言~