導語

關於質數的未解之謎一直困擾著數學家，例如，著名的孿生質數猜想認為存在無窮多對相差2的質數，黎曼猜想試圖揭示質數的分佈規律。半個多世紀之前，一位數學家為解決這些更困難的問題提出了一個墊腳石問題：一個整數有奇數還是偶數個質因數，與它前後的整數是有奇數還是偶數個質因數沒有關聯。然而，證明這個墊腳石問題本身同樣困難重重。著名數學家陶哲軒用擴充套件圖作為工具不那麼精確地證明了這個猜想的一個簡單版本。最近，兩位數學家進一步提出了一個更強大、更普適的證明，表明圖論在解決數論問題上的強大威力。

研究領域：圖論，數論，隨機遊走

一項新的證明揭穿了一個陰謀，數學家曾擔心它會像烏雲一樣盤旋在數軸之上。而在證明過程中，數學家們開發了另一套工具來理解算術的基本組成部分——質數。

在2021年3月發表的一篇論文中，德國哥廷根大學的 Harald Helfgott 和加州理工學院的 Maksym Radziwiłł 提出了一個改進的解決方案，以解決喬拉猜想（Chowla conjecture）的特定表述——這是一個關於整數之間關係的問題。該猜想預測，一個整數是有奇數還是偶數個質因數，並不影響它前後的整數是有奇數還是偶數個質因數。也就是說，相鄰整數的某些最基本的算術屬性不會有特定方式的關聯。

這個看似簡單的想法與數學中一些關於質數的最深刻問題交織在一起。加州大學洛杉磯分校的陶哲軒（Terence Tao）說，證明喬拉猜想是回答這些更棘手問題的“熱身或者說墊腳石”。

然而幾十年來，這樣的熱身問題本身就成了一項幾乎不可能完成的任務。數學家們也是在短短几年以前才取得了一些小小進展，當時陶哲軒證明了這個問題的一個更簡單的版本，稱為對數喬拉猜想（logarithmic Chowla conjecture）。雖然他使用的技術被認為富有創新性且令人興奮，但得到的結果不夠精確，無法幫助在相關問題上取得更多進展，包括關於質數的問題。數學家希望還能有一個更強大、更普適的證明。

圖1.

陶哲軒開發了一種策略，使用擴充套件圖（expander graph）來回答喬拉猜想的對數版本，但該策略目前無法完全發揮作用。| 來源：加州大學洛杉磯分校

現在，Helfgott 和 Radziwiłł 提供了這樣一個證明。他們的解決方案將圖論（graph theory）技術直接推向數論（number theory）的核心，重新點燃了喬拉猜想兌現其承諾的希望——為數學家提供最終引導他們解決一些最難以捉摸問題所需要的想法。

1. 質數的陰謀

當數學家思考乘法和加法在質數方面的關係時，數論中許多最重要的問題就會出現。

質數本身是用乘法定義的：它們不能被除自身和 1 以外的任何數字整除；它們相乘則會構成其餘的整數。但是幾個世紀以來，涉及加法的質數問題一直困擾著數學家。例如，孿生質數猜想斷言有無窮多個相差 2 的質數（如 11 和 13）。這個問題連線了乘法和加法兩個通常相互獨立的算術運算，因而具有挑戰性。“這很困難，因為我們混合了兩個世界，”布里斯托大學的 Oleksiy Klurman 說。

直覺告訴數學家，一個數加 2 應該完全改變它的乘法結構——這意味著一個數是否是質數（一種乘法性質）和兩個單位之外的數是否是質數（一種加法性質）之間應該沒有相關性。數論家沒有發現任何證據表明存在這種相關性，但如果沒有證明，他們也不能排除相關性出現的可能性。

“據我們所知，一個巨大的陰謀可能存在：每當一個數 n 決定成為質數時，它都會與鄰居 n + 2 達成某種秘密協議，讓它不再被允許成為質數”，陶哲軒說。

沒有人接近排除這樣的陰謀。這就是為什麼在 1965 年，喬拉（Sarvadaman Chowla）制定了一種稍微簡單的方法來思考鄰近數字之間的關係。他想證明，一個整數是具有偶數或奇數個的質因數——這一條件被稱為其質數數量的“奇偶性”（parity）——不應該以任何方式影響其相鄰整數質因數的數量。

這個陳述通常用劉維爾函式（Liouville function）來理解，如果整數有奇數個質因數（如 12 = 2 × 2 × 3），則它為整數賦值 -1；如果整數有偶數個質因數（如 10 = 2 × 5），則它為整數賦值 +1。喬拉猜想預測，劉維爾函式的相鄰取值之間應該沒有相關性。

圖2. 前10個整數的劉維爾值，及其質因數分解的離散圖。

例如 6 = 2x3，有偶數個質因數，劉維爾值為 +1，8 = 2x2x2，有奇數個質因數，劉維爾值為-1。| 來源：譯者繪製 [1]

在探究奇偶性時，許多研究質數的最先進方法都失敗了，而喬拉猜想正是要研究奇偶性問題。數學家希望透過解決這個問題，可以發展出新想法應用於諸如孿生質數猜想等問題。然而，多年來，它仍然只是一個幻想中的希望。不過，在 2015 年，一切開始改變。

2. 意外突破：奇偶簇煙消雲散

芬蘭圖爾庫大學的 Radziwiłł 和 Kaisa Matomäki 並沒有著手解決喬拉猜想。相反，他們想研究劉維爾函式在一段短區間上的行為。他們已經知道，該函式的取值在整個正整數域上平均來看為 +1， -1各半；但它的值仍然有可能聚集在一起，在某個較長的連續區間內的取值要麼全部為 +1，要麼全部為 -1，從而形成團簇。

圖3. 為1至n之間的整數統計劉維爾值的平均值，n 截止至10000的對數線性圖。

隨著n增大，統計值逐漸逼近0，表明函式取值趨近 +1， -1 各半。| 來源：譯者繪製 [1]

2015 年，Matomäki 和 Radziwiłł 證明這些團簇幾乎從不出現。他們於次年發表的研究表明，如果選擇一個隨機數並檢視它的成百上千個最近鄰，大約一半整數的質因數數量是偶數，另一半是奇數。

圖4. 為1至n之間的整數按其劉維爾值分組，統計下一個數的劉維爾值平均值，n 截止至10000的對數線性圖。

不論是哪一組，統計值都在逼近0，這可以提供關於喬拉猜想的直覺。| 來源：譯者繪製 [1]

“這是拼圖中缺少的重要部分，”蒙特利爾大學的 Andrew Granville 說。“他們取得了令人難以置信的突破，徹底改變了整個主題。”

這是一個強有力的證據，提示數字並不是上述大規模陰謀的同謀——不過，喬拉猜想是延伸到整個數軸的最高級別的陰謀。這就是陶哲軒進入的地方。幾個月後，他發現一種方法可以在 Matomäki 和 Radziwiłł 工作的基礎上解決一個更容易研究的問題，即對數喬拉猜想。在這個公式中，較小的數字被賦予較大的權重，以便與較大的整數一樣被取樣。

陶哲軒試圖用反證法證明對數喬拉猜想。首先，他假設對數喬拉猜想是錯誤的——事實上，連續整數的質因數數量之間存在一個陰謀。然後他試圖證明這樣的陰謀可以被放大：喬拉猜想的一個例外不僅意味著連續整數之間的陰謀，而且意味著沿著整個數軸的更大陰謀。然後，他就能夠利用 Radziwiłł 和 Matomäki 早先的結果，它恰好排除了這種更大的陰謀。喬拉猜想的反例會導致邏輯上的矛盾——從而證明反例不可能存在，猜想必須為真。

但在陶哲軒能做上述任何推理之前，他必須想出一種連線數字的新方法。

3. 圖——連線數字

陶哲軒首先利用了劉維爾函式的一個定義特徵。考慮數字 2 和 3，兩者都有奇數個質因數，因此劉維爾值都為 -1。但因為劉維爾函式是乘法的，所以 2 和 3 的倍數也有相同的符號模式。

這個簡單的事實具有重要的含義。如果2 和 3 都有奇數個質因數是由於某種秘密陰謀，那麼 4 和 6 之間也存在陰謀——數字相差不是 1，而是相差 2。由此開始事情變得更糟：相鄰整數之間的陰謀也意味著其所有倍數對之間的陰謀。“對於任何質數，這些陰謀都會隨倍數放大而傳播開來。”陶哲軒說。

為了更好地理解這個不斷擴大的陰謀，陶哲軒從圖的角度來思考它，圖是由邊連線的頂點的集合。在這個數字圖中，每個頂點代表一個整數。如果兩個數相差一個質數並且也能被該質數整除，則它們由一條邊連線。

例如，考慮數字 1001，它可以被質數 7、11 和 13 整除。在陶哲軒的圖中，它與 1008、1012 和 1014（透過一次加法）以及 994、990 和 988（透過一次減法）共享邊。這些數字中的每一個依次連線到許多其他頂點。

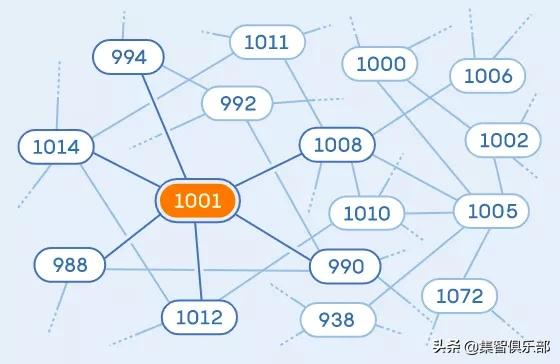
圖5. 陶哲軒的圖中，每個頂點代表一個整數。如果兩數相差一個質數並且也能被該質數整除，則它們由一條邊連線

圖6. Harald Helfgott 和 Maksym Radziwiłł 設計了一種簡單的圖來研究整數。

整數之間只要相差一個質數就會連線。他們證明這個圖逼近於上面的圖，這兩個圖都編碼一個大到不可能為真的陰謀。| 來源：Samuel Velasco/Quanta Magazine

總而言之，這些邊編碼了更廣泛的影響網路：彼此連線的數字代表喬拉猜想的例外情況，其中一個整數的因式分解實際上確實會影響另一個的。

為了證明喬拉猜想的對數版本，陶哲軒需要證明這個圖有太多連線，不能真實地表示劉維爾函式的值。用圖論的語言來說，這意味著證明他的互連數字圖是一個“擴充套件”圖。

4. 拓展圖上的隨機遊走

擴充套件圖是衡量陰謀範圍的理想標準。這是一種高度連通的圖，儘管與頂點數量相比，邊相對較少。這使得建立一個與圖的其他部分沒有太多互動的相互連線的頂點簇變得很困難。

如果陶哲軒能證明他的圖是一個區域性擴充套件圖——圖上的任何給定鄰域都具有這個屬性——他將證明對喬拉猜想的一次違背將傳播到整個數軸上，這明顯違反了 Matomäki 和 Radziwiłł 在2015年的結果。“獲得相關性的唯一方法是，讓整個群體都具有這種相關性。”陶哲軒說。

對一個圖是否為擴充套件圖的證明，通常可以轉化為研究沿其邊的隨機遊走。在隨機遊走中，連續的每一步都是偶然決定的，就像在城市中漫步，並在每個路口擲硬幣來決定是左轉還是右轉。如果那個城市的街道形成一個擴充套件圖，那麼透過比較少的幾步隨機遊走，就幾乎可以到達任何地方。

但是在陶哲軒的圖上游走是奇怪而迂迴的。例如，不可能直接從 1001 跳到 1002，這需要至少經過另一箇中間數。沿著這個圖的隨機遊走從一個整數開始，加或減一個能夠整除它的隨機質數，然後移動到另一個整數。

重複這個過程幾次並不明顯能導向給定鄰域中的任何點，但如果圖真的是擴充套件圖，情況應該是這樣。事實上，當圖上的整數變得足夠大時，甚至連隨機路徑如何建立都不再清楚：將數字分解為它們的質因數，從而定義圖的邊，變得異常困難。“計算所有這些遊走，會是一件可怕的事情。” Helfgott 說。

當陶哲軒試圖證明他的圖是一個擴充套件圖時，“這有點太難了，”他說。不過他開發了一種新方法，基於熵這種對隨機性的度量。這使他能夠避免展示擴充套件圖屬性的需要——但需要付出代價。他可以解決對數喬拉猜想，但不如他想的那麼精確。在猜想的理想證明中，整數之間的奇偶獨立性應該總是很明顯，即使沿著數軸的一小部分。但是在陶哲軒的證明中，直到取樣了天文數字量級的整數，這種獨立性才變得明朗。“量化來看，它不是很強大。”圖爾庫大學的 Joni Teräväinen 說。

此外，他的熵方法如何擴充套件到其它問題上仍然不清楚。牛津大學的 James Maynard 說，“陶哲軒的工作是一個徹底的突破，”但由於這些限制，“它不可能給出更多東西自然引導我們到問題的下一步，比如孿生質數猜想。”

五年後，Helfgott 和 Radziwiłł 設法做到了陶哲軒無法做到的事情——進一步擴大他發現的陰謀。

圖7.

Maksym Radziwiłł（左）和 Harald Helfgott（右）研究了擴充套件圖上的隨機遊走，以證明關於連續整數的質因數分解的強陳述。| 來源：加州理工學院；洪堡基金會/Sven Müller

5. 樸素圖幫助擴大陰謀

陶哲軒建立一個圖的方法是，若兩個整數相差一個質數並且可以被該質數整除，則在它們之間連一條邊。而 Helfgott 和 Radziwiłł 考慮了一種新的“樸素”圖（naïve graph），它拋棄了第二個條件，即只要兩個整數相差一個質數，就可以建立一條連邊。

直接結果是邊的數量爆炸式增長。在這個樸素圖上，整數 1001 與其他頂點的連線不是隻有6個，而是有數百個。另一方面，這種圖在一個關鍵方面卻比陶哲軒的圖簡單得多：沿其邊隨機遊走，不需要知道非常大整數的質因數。這兩個方面共同作用，使得證明樸素圖中的任何鄰域都具有擴充套件屬性變得更加容易——你很可能透過很少幾步隨機遊走就能從一個頂點到達任何其他頂點。

Helfgott 和 Radziwiłł 需要證明這個樸素圖逼近於陶哲軒的圖。如果他們能證明這兩個圖是相似的，就可以透過研究樸素圖來推斷陶哲軒的圖的屬性。而且因為他們已經知道樸素圖是區域性擴充套件圖，就可以推斷陶哲軒的圖也是（因此對數喬拉猜想為真）。

但是考慮到這個樸素圖比陶哲軒的圖的邊多得多，如果存在相似之處，它也被掩埋了。“當你說這些圖看起來很像時，這將意味著什麼？” Helfgott 說。

6. 矩陣揭示隱藏的相似性

雖然這兩種圖在表面上看起來並不像，但 Helfgott 和 Radziwiłł 透過在兩個視角之間轉換來證明它們彼此逼近。一方面，他們將圖視為圖；另一方面，他們將圖視為矩陣這種數學物件。

首先，他們將圖表示為一個矩陣，這個矩陣是編碼頂點之間是否有連邊形成的數字陣列。然後他們從代表陶哲軒圖的矩陣中減去代表樸素圖的矩陣，結果是一個代表兩者之間差異的矩陣。

Helfgott 和 Radziwiłł 需要證明，與該矩陣相關的特定引數（稱為特徵值）都很小。這是因為擴充套件圖的一個定義特徵是它的鄰接矩陣具有一個大的特徵值，而其餘的則明顯更小。如果陶哲軒的圖和樸素圖同樣是擴充套件圖，那麼它也會有一個大的特徵值——當從一個矩陣中減去另一個矩陣時，這兩個大的特徵值幾乎會抵消，留下一組都很小的特徵值。

但是特徵值本身很難研究。相反，證明該矩陣的所有特徵值都很小的等效方法又會回到圖論。因此，Helfgott 和 Radziwiłł 將這個矩陣（代表他們的樸素圖的矩陣與陶哲軒的更復雜的矩陣之間的差異）轉換回了一個圖。然後，他們證明這個圖包含很少的會迴圈回到起點的隨機遊走（具有特定長度並且符合少數其他屬性）。這意味著陶哲軒的圖上的大多數隨機遊走基本上抵消了樸素擴充套件圖上的隨機遊走——這意味著前者可以被後者逼近，因此兩者都是擴充套件圖。

7. 圖幫助洞察隱秘結構

Helfgott 和 Radziwiłł 對對數喬拉猜想的解決方案標誌著對陶哲軒結果的顯著量化改進。他們可以對更少的整數進行取樣就能得出相同的結果：一個整數的質因數數量的奇偶性與其鄰居的奇偶性不相關。

牛津大學的 Ben Green 說：“這是解釋質數和可除性看起來為何隨機的一個非常有力的陳述。” 但這項工作可能更令人興奮，因為它提供了“一種解決問題的自然方法” ，Matomäki 說——這正是陶哲軒六年前最初希望的直觀方法。

擴充套件圖之前已經在理論計算機科學、群論和其他數學領域帶來了新發現。現在，Helfgott 和 Radziwiłł 也將它們用於數論問題。他們的工作表明，擴充套件圖有能力揭示算術的一些最基本屬性——消除潛在的陰謀，並開始解開加法和乘法之間複雜的相互糾纏。

Maynard 說：“突然之間，當使用圖這種語言時，它會在問題中看到你事先無法真正看到的所有這些結構。這就是奧妙所在。”

Jordana Cepelewicz | 作者

徐恩嶠 | 譯者

梁金 | 審校

鄧一雪 | 編輯

商務合作及投稿轉載｜[email protected]
◆ ◆ ◆

搜尋公眾號：集智俱樂部

加入“沒有圍牆的研究所”

讓蘋果砸得更猛烈些吧!