隨著科技的不斷髮展,我們的生活也越來越便捷,特別是進入網際網路時代,人們利用移動裝置進行支付、資訊檢索等也成了大勢所趨。不是有一句話說得好嘛,移動支付的出現把小偷都逼到失業了!
今天我們來講一講作為網際網路時代的產物——二維碼。
二維碼的出現給我們日常生活帶來了許多的便利,除了日常的掃碼支付以外,二維碼還能夠實現資源之間更高效地傳遞交流,可謂是人類智慧的結晶。
但是你知道嗎,據不完全資料統計,全球每天消耗的二維碼的數量將近100個億。
相信看到這裡很多朋友都會疑惑,二維碼作為一種排列組合出來的圖案,它的排列組合方式一定是有限的,一天就有如此之多的二維碼被消耗掉,那是不是再過幾年所有的二維碼都會被耗盡?二維碼都用完了我們接下來用什麼?
要回答這個問題,首先我們要來了解一下二維碼。
二維碼是如何產生的?
首先,二維碼的產生必然是經濟發展的需求所推動的。
初代的“二維碼”其實就是我們所說的條形碼(又叫做一維碼),上個世紀五十年代日本人為了解決收銀員用手寫記錄商品售賣情況而引起的結賬效率慢的問題,發明了條形碼。
條形碼原理是利用黑白兩個反射率不同的色條組成的,透過對其掃描之後光的折射結果不同,從而識別出它所包含的資訊。此後在很長一段時間內,條形碼被廣泛地使用,但這也出現了一個問題,隨著經濟快速地發展,人們對於資訊儲存的需求也在不斷擴大,條形碼在一定大小內儲存容量有限,它已經無法滿足人們的發展需求了。
就在1994年,一個男人帶著一維碼“plus”版橫空出世了,這個人就是“二維碼之父”——一個叫做騰弘原的日本人。
騰弘原在原有的基礎上對條形碼做出了改革,從外觀上面我們就能很明顯地看出,二維碼和條形碼最大的差別就是形狀的不同,條形碼都是豎條狀平行分佈的,負載資訊的是色條;而二維碼是矩陣式的點狀分佈,它負載資訊的則是色塊。
它們功能上的差別也就在於,條形碼只能夠在水平方向上表達資訊,而二維碼能夠在水平和垂直兩個方向上儲存和表達資訊。
所以由於二維碼更具有實效性,它也逐漸取代了條形碼的位置,在日常生活中被人們廣泛地使用。
“0”和““1”的二進位制編碼
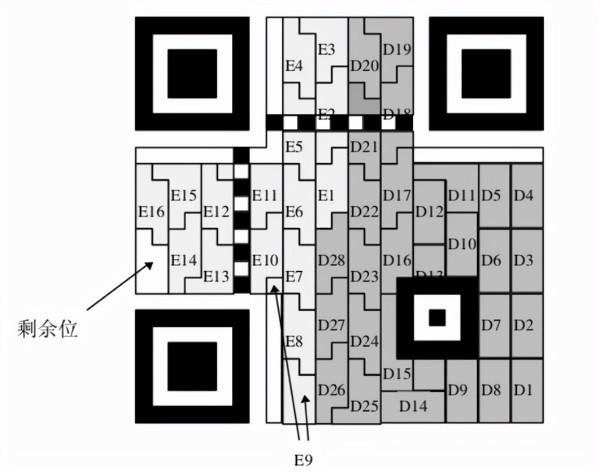
一個有效的二維碼其實就是一個矩陣,矩陣的規格不同自然二維碼的大小也不同,人們利用電腦中的程式手段對矩陣進行繪製,最後形成出來的不同內容的矩陣圖案就是我們所熟悉的二維碼了。
簡單點來說就是對一個矩陣裡面的方塊進行的填充,並且這每一個方塊都攜帶了一定的資訊片段,將這些資訊片段組合在一起就能夠得到完整的資訊。
既然是二維碼是矩陣中方塊排列組合的結果,那麼從理論上來說,二維碼一定會有消耗完的一天。
那“這一天”是多久呢?
我們用目前最小規模的21*21矩陣來演算一下,這個矩陣一共包含了21*21也就是411個方塊,每一個方塊可以被命名成“1”或者是“0”,我們可以在矩陣內任意地填塗,那麼這個矩陣一共可以有2的411次方種排列組合的可能性,也就是大約是56萬億種可能。
除此之外,25*25規模矩陣的二維碼也是我們日常所使用頻率最多的,不算上矩陣中用於定位的方塊、用於糾錯的方塊以及多餘無意義的方塊,它裡面一共包含了478個有意義的點,那麼25*25規模的二維碼就一共有2的478次方組合結果,這個結果有多大呢?
這裡我們引入一個冪函式的概念:“同底數冪相除,底數不變,指數相減”,也就是a^m/a^n=a^(m-n)。2的478次方就是一個冪函式,2是它的底數也就是公式裡面的a,478是它的指數,即m。
我們現在已經知道了2的411次方(也就是公式裡的n)的結果,所以根據以上的運演算法則,我們就只需要知道2的67次方的結果,再把2的411次方的結果與2的67次方的結果相乘,就可以得出2的478次方的最終運算結果。
21*21矩陣有2的411次方大約等於是56萬億,2的67次方等於147573952589676412928,兩者相乘就是25*25規模矩陣的二維碼所有排列組合的結果數量,這個資料有多麼地驚人,相信大家也看到了。
有朋友會說,直接說2的478次方不就行了嗎?為什麼非要弄得那麼複雜?
一是2的411次方的結果太大,我無法給出一個準確的資料;二是因為,用這樣拆分的方法能夠讓朋友們直觀地感受到資料之大。
如果說上面的資料還不足以說明二維碼可用的數量之大,那我們用一個更加直觀的例子來說明。
上面已經說到了21*21規模的矩陣有2的411次方種可能,這個資料太大算起來十分困難,在這裡就不給出具體的資料了。我們就取它的一部分來看,從而推理類比出來最後的結果。
2的60次方的結果是115萬億,把這一部分數量的二維碼平均分給全球78億人,那麼每個人能夠得到每個人可以得到大約1647萬個二維碼,假設每人每天使用20個二維碼,那麼一個二年用完這些二維碼大概需要2256年。
2256年,這個數字夠直觀了吧?人才能夠活多少歲?
假設一個人能夠活到一百歲,要用完這1647萬個二維碼,那麼每天就要452個二維碼。
正常情況下,誰會一天用得完452個二維碼?
而這僅僅不過是2的60次方所推算出來的結果,只是二維碼數量的冰山一角。
所以,我們再回到開頭的問題,全球每天消耗100億個二維碼,二維碼會不會用完?
答案是當然會用完,不過全部用完是需要一個非常非常非常漫長的時間。
如果說沒用完的二維碼繼承下來是一種財富,那人人都可以是富N多代了。
看到這裡,可能有的朋友還會有一個疑問,世界上兩個有沒有相同的二維碼呢?
或者換句話說,二維碼的使用壽命那麼低,能不能重複利用呢?
理論上來說,這種可能確實是有的。
但如果想要出現相同的二維碼,那麼只有在不同的系統之下才能夠生成(因為同一個系統中肯定是不會生成相同的排列組合結果的)。
所以這兩個相同的二維碼它們所承載的資訊肯定是完全不同的,用這個解釋我們就能知道,為什麼我們在進行移動支付的時候,支付寶的系統掃不出來微信二維碼的資訊。
況且,二維碼的數量那麼龐大,根本沒有必要使用兩個重複的二維碼來避免“浪費”。
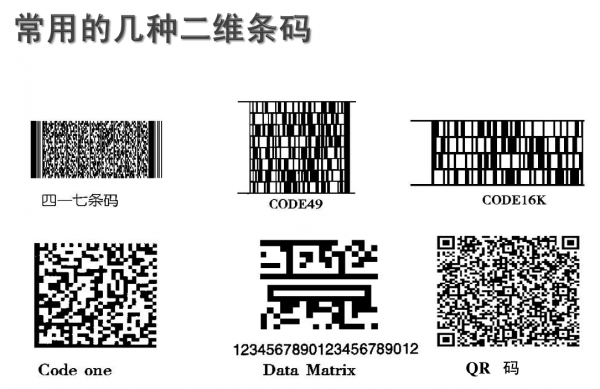
其實經過了幾十年的不斷髮展,二維碼從規格上、版本上都在進行不斷的革新,常見二維碼種類有Data Matrix、MaxiCode、Aztec、QR Code、PDF417、Vericode、Ultracode、Code 49、Code 16K,上面我們說到二維碼只是QR Code這一種格式。
朋友們,請你們想一下,光是一種格式的二維碼都夠我們用上無窮無盡的時間,更不要提還有那麼多種格式的二維碼了!
所以,我們根本不用擔心二維碼用不用得完這個問題。雖然理論上它的數量一定是有限的,但它的“有限”在人類發展歷史中幾乎趨近於“無限”,就算是刷到所有海水都乾枯、所有石頭都爛掉了都刷不完所有的二維碼。
拿近了來說,以人類聰明的智慧,二維碼的更新換代技術勢頭猛如虎,這幾年不是連靜態二維碼還沒用完呢,這又出了動態二維碼了嗎。
照著這勢頭髮展下去,說不定過幾年就會出現“三維碼”、“四位碼”了呢?
作者 露絲 初審:小晞 校稿編輯:李子