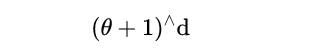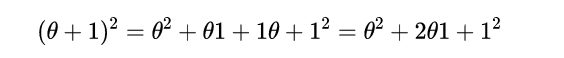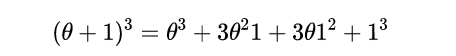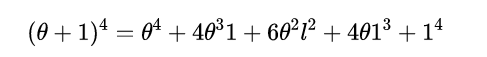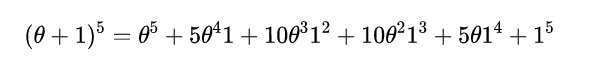代數和超立方體
我們都熟悉正方體,它們是空間的基本幾何實體。以某種方式表示,立方體的頂點包含了所有可以用數字0和1構造的點(後面我會解釋)。因此,(超)立方上的每一點都可以用下列代數展開式來表示:
例如,讓我們從d=2開始,立方體是一個正方形。我們得到:
這些項都可以在一個正方形上視覺化,如下所示(用0替換θ,用1替換l;所以θ^2對映到(0,0),θl對映到(0,1),依此類推)。請注意,θl和lθ項結合在一起,位於黃線上。黃線的方程是x+y=1。
- 圖1:正方形上的代數係數。
接下來,我們轉移到三維空間,看看一個立方體。代數表示式變成了:
θ^2l係數的三項組成了下面圖2中的紫色等邊三角形,而θl^2係數的三項構成了橙色的等邊三角形。紫色平面的方程是x+y+z=1,橙色平面的方程是x+y+z=2(從各自平面上的點可以看出)。
- 圖2:立方體上的代數係數
到目前為止,我們已經在這些立方體的切割平面上看到了一些線和一些等邊三角形。我們需要快速回顧一下柏拉圖實體的情況。
廣義的柏拉圖立體(多面體)
柏拉圖立體是非常的對稱物體。五個柏拉圖實體存在於三維空間,六個存在於四維空間。你會期望5維和6維空間的數量可能更多,但事實上所有大於4的維度都只有3個柏拉圖立體。 那麼,存在於所有維度空間的這3個柏拉圖實體是什麼?
正方體
我們已經研究了正方體,它屬於柏拉圖立體。由於它是用來測量空間的,所以它必須存在於所有維度。在d維空間中,它將有2^d個頂點。
八面體
在立體幾何中,有一個對偶立體的概念。選取一個立體,並考慮每個面的中心(如果實體是在d維空間,面就是d-1維的)。現在,你將這些面的中心視為頂點,並構建一個新的實體,從而形成開始時立體的對偶。八面體就是立方體的對偶實體。在二維空間中,我們得到一個正方形,透過連線所有邊的中點得到對偶,就是另一個正方形。
- 圖3:在二維空間中,正方形的對偶還是正方形。
在三維空間中,事情變得更加有趣,我們在取立方體的對偶時得到了一個新的立體。請看下面的圖。由於立方體有6個面,所以八面體最終有6個頂點。
- 圖4:八面體是立方體在三維空間的對偶。
由於立方體存在於所有維度,其對偶八面體也存在於所有維度。
四面體
四面體實際上是最簡單的立體。考慮一組點(實體的頂點),它們都是相互等距的。如你是在二維空間,這種點的最大數量可能是3個,它們形成一個等邊三角形。在三維空間中,可以從等邊三角形的中心點開始,把它提升到第三維,直到它與前面三個點的距離一樣遠。這個過程可以隨著我們增加維度而無限地重複,事實證明,有可能將(d+1)個點放在d維空間中,使它們都相互等距離。做到這一點的唯一方法是把它們放在廣義四面體的頂點上。
- 圖5:3維空間的四面體。白色的點是藍色等邊三角形的中心點,沿著第三維度提升。
四維立方體的切面
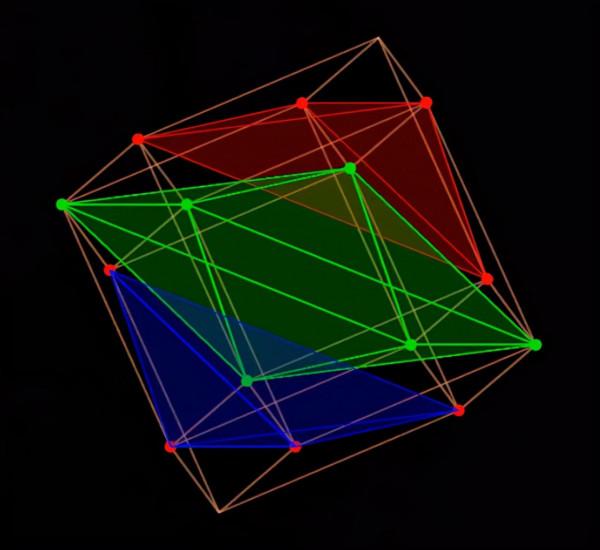
現在我們有了柏拉圖立方體的概念,我們可以繼續前進,從三維空間到四維空間,一個四維的立方體被稱為超立方體(魔方)。和之前一樣,我們從代數開始:
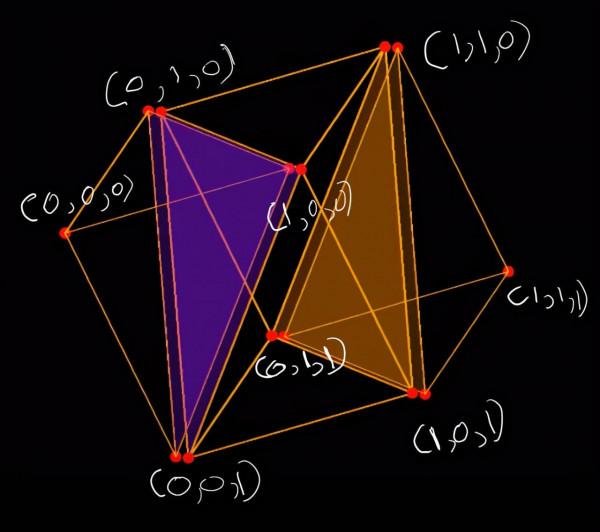
事實證明(即將解釋),構成θ^3l係數的四個項位於x+y+z+w=1平面上,形成一個四面體,構成θl^3係數的四個項也是如此。構成θ^2l^2係數的六個項形成一個八面體,這在下圖中顯示。令人難以置信的是,這些三維柏拉圖立體居然隱藏在四維的on=e中。
回到三維空間
形成藍色四面體的頂點位於x+y+z+w=1的平面上,每個頂點都包含三個0和一個1(1的位置是它們四個之間的區別)。可以清楚地看到,它們之間的距離都是一樣的。而根據上一節,這意味著它們必須形成一個四面體。
對於形成紅色四面體的四個頂點,也可以做類似的論證,它們位於平面x+y+z+w=3上,由3個1和1個0組成。
構成綠色八面體的頂點位於平面x+y+z+w=2上,因此它們的座標中有兩個0和兩個1。這6個點是2個0和2個1的排列方式,也就是4!/(2!2!) = 6。很容易看出,這六個點中的每一個點與其他四個點的距離都是sqrt(2),與剩下的一個點的距離是2(例如:[0,0,1,1]與[1,0,1,0]、[0,1,1,0]、[1,0,0,1]的距離是sqrt(2),約為1.414,而與[1,1,0,0]的距離是2)。這個剖面與八面體完全吻合。
有兩個重要的事情需要提出。
- 首先,沿著這些切片平面形成實體的各種點,只是一些0和1的排列組合。上圖中的藍色四面體是由[0,0,0,1]的排列組成的,綠色八面體是由[0,0,1,1]的排列組成的,紅色四面體是由[0,1,1,1]的排列組成的。
- 第二,在任何維度的空間中,第一個切割面x+y+...=1將包含點[0,0,...,1]的排列組合。這些點都將是彼此等距的。因此,與第一個平面(x+y+...=1)相交的d維立方體的點將總是形成一個(d-1)維的四面體。另外,由於我們只是對0和1的陣列進行置換,所以我們永遠不會改變陣列的總和。因此,如果我們考慮的超立方體是d維的,沿著切片的實體將位於(d-1)維。這就是為什麼我們對一個普通立方體的切片得到2維的形狀,而當我們對一個4維立方體切片時得到3維的實體。
那麼,是否像迄今為止的觀察所表明的那樣,我們總是從這些型別的切片平面中得到柏拉圖式的實體?
讓我們考慮一下五維立方體。從代數擴充套件開始:
θ^5和l^5分別對映到(0,0,0,0,0)和(1,1,1,1)。與5θ^4l項相對應的5個點是[0,0,0,0,1]的排列組合,由於它們彼此之間的距離相等,所以形成了一個四邊形的四面體。同樣地,5θl^4也形成一個四面體。但是由10θ^3l^2項形成的立體呢?這10個點是[0,0,0,1,1]的排列組合。這也是一個柏拉圖式的立體嗎?沒有10個頂點的四維柏拉圖立體,所以這不可能是真的。這有點讓人失望,但也讓人興奮。失望是因為到目前為止,用0和1組成的陣列的排列組合總是能得到柏拉圖式的立體,但這個觀察結果不成立。令人興奮的是,我們現在可以探索用這種方法發掘出的各種立體。對於有10個頂點的四維空間的神秘立體,我們可以研究它的屬性,但不能想象出它的樣子,因為我們的大腦是針對三維世界的。為了得到更多我們可以用大腦思考的令人興奮的三維立體,我們需要回到對四維立方體的切割上。我們已經嘗試了超立方體,而且產生了三個柏拉圖實體(兩個四面體和一個八面體)。我們還能得到什麼?
更大的立方體
我們已經從四維立方體中提取了所有的三維立方體。為了探索其中更多的東西,我們需要把超立方體維度變大,這時已經很難視覺化。為了保證我們得到的切片是3維的,我們必須堅持4維空間。
如果我們堅持相同的維度空間,但仍然想讓立方體變大,我們必須增加邊的長度。因此,我們不再是一個單位立方體,而是讓它變成2個單位。這是一個很大的變化,所以讓我們看看它在三維空間中是什麼樣子。
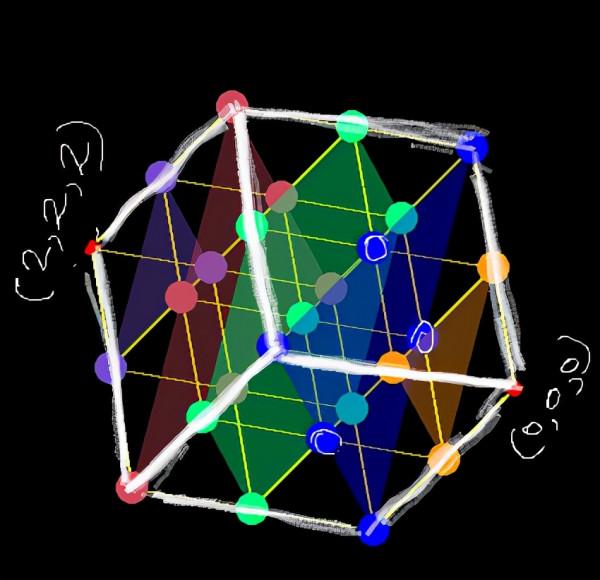
回到三維空間
與圖2相比,我們得到了相當多的切割平面,你可以在下面看到。橙色平面對應x+y+z=1,藍色平面對應x+y+z=2,綠色平面對應x+y+z=3,紅色平面對應x+y+z=4,紫色平面對應x+y+z=5。
- 圖7:邊長為2個單位的三維立方體的切割面
讓我們回到代數上。之前,我們用θ代表0,用l代表1。現在我們也有了2,讓我們用變數τ來代表它。代數表示式就變成了:
首先要注意的是,除了θ^3和τ^3項只是代表點[0,0,0]和[2,2,2]之外,還有其他8項。然而,只有5個平面。這表明,這些點的集合中有許多一定是共享相同的平面。事實上,考慮一下3θl^2項中代表[0,1,1]、[1,1,0]和[1,0,1]的三個點,以及3θ^2τ中代表[0,0,2]、[0,2,0]和[2,0,0]的三個點。前三個是上圖中用白色圈起來的藍色點,後三個是沒有用白色圈起來的三個藍色點。很明顯,它們兩組都位於平面x+y+z=2上。這在單位立方體中是不可能的,因為那裡的點只由0和1組成。因此,每個代數擴充套件項都有一個平面(如3θ^2l),其他項的點都不會到裡面。現在,我們能夠透過包括兩個1(或一個θl^2項)或一個2(一個θ^2τ項)使座標加到2。因此,平面共享成為一件事。
但這沒有關係,我們仍然可以提出這樣的問題:在代數式展開中,這些項會形成什麼形狀。例如,來自3θl^2項的[0,1,1]、[1,1,0]、[1,0,1]和來自3θ^2τ項的[0,0,2]、[0,2,0]的兩組點都形成等邊三角形(剛好共享同一個平面)。事實上,是否有可能從展開的項中得到所有可能的形狀?我們知道,代數式展開中的任何項都是由一些整數陣列的排列組合的點組成的。在三維空間中,陣列的長度為三個元素》有三種可能性:
- 陣列的所有三個元素都是不同的。例如:[0,1,2]
- 兩個元素是相同的,第三個元素是不同的。例:[0,0,1]
- 所有三個元素都是相同的。例子:[0,0,0]
對於第三種情況,只有一個可能的點,所以我們根本沒有得到一個立體。對於第二種情況,會有三個這樣的點的排列組合,這三個排列組合所對應的點會形成一個等邊三角形。對於第一種情況,將有六個排列組合,這六個點將形成一個六邊形。而這正是圖7中間的綠色六邊形的情況。就3維空間的不同可能性而言,圖7中都有涉及,就是這樣了。你可能會問,如果我們使用除0、1和2之外的其他整數會怎樣?事實證明,除了上述情況1、2和3之外,增加其他型別的整數不會改變可能的基本形狀,你可以自己去驗證。
然而,立方體中包含的實際平面可能是不同的,因為它們是由一組以上的代數項組成的。下圖顯示了一個更大的立方體的平面情況,每個邊的尺寸為6個單位。
- 圖8:邊長為6的立方體的切割平面。
再談四維空間
我們知道,切開一個三維立方體,會得到位於平面上的點,這些點可以形成等邊三角形或正六邊形。我們對切開4維立方體所形成的3維立體更感興趣。我們已經看到了切割單位四維立方體得到的東西:一個四面體和一個八面體。但退一步講,我們知道點的座標將是四維整數陣列。這裡有一些可能性:
- 所有的元素都是不同的。例如:[0,1,2,3]。這些點的排列組合:4! = 24.
- 兩個元素是相同的,另外兩個是不同的。例如:[0,0,1,2]。這樣的點的排列組合:4!/2! = 12.
- 兩個元素是相同的,另外兩個也是相同的,但與前兩個不同。例如:[0,0,1,1]。這種點的排列組合:4!/(2! 2!) = 6.
- 三個點是相同的,最後一個點是不同的。例如:[0,0,0,1]。這樣的點的排列組合:4!/3! = 4.
- 所有四個點都是一樣的。例如:[0,0,0,0]。這樣的點的排列組合:1.
這就窮盡了所有的可能性。第5種情況是不值一提的,我們只得到一個點。情況4是我們在切割四維立方體並得到四面體時已經看到的情況。情況3也是,當時我們在中心得到一個八面體。讓我們像對3維情況那樣擴大4維立方體的大小。代數表示式變成:
這裡不再列出所有的15個項,它們是一堆四面體和八面體。除了上面案例2中形成立體的兩個項,有12個頂點;12θ^2lτ和12θlτ^2。這些可能會形成什麼樣的立體?二十面體是一個具有12個頂點的柏拉圖式立體,那麼會不會是這個呢?繪製形成這些點的近鄰的邊(由[0,0,1,2]的排列組合形成),並投射到二維空間,我們得到以下形狀:
- 圖9:由[0,0,1,2]的12個排列組合形成的圖形。這就是截斷的四面體,一個阿基米德立體。
它本質上是一個被切掉四個角的四面體。它屬於一個立體家族,是僅次於柏拉圖式立體的東西,即阿基米德式立體。在三維空間中只有13個這樣的立體,它們與柏拉圖立體完全一樣,只是可以有多種不同型別的正多邊形組成面(在這裡,有三角形和六邊形)。
開放性問題
我將給你留下一些在本文中沒有回答的問題。我也不知道答案(感知難度的增加)。
- 透過一個五維立方體,我們在四維空間有某種具有10個頂點的立體,我們從未進一步探索過。這可能是4維空間中的某種阿基米德立體嗎?
- 對於在超立方體的切割超平面上發現的這類立體,我們能說點什麼嗎?我們知道它們可以是但不一定是柏拉圖式的,而且它們可以是阿基米德式的。還有什麼其他的可能性嗎?
- 我們知道5維及以上維度的柏拉圖實體的數量總是3。對於更高維度上的阿基米德立體,有多少個?在4維中有多少個?