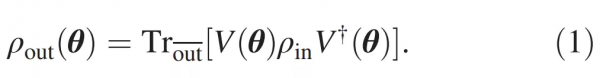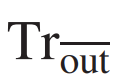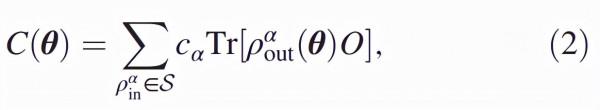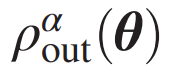機器之心報道
編輯:小舟
許多人質疑量子資料能否變得高度可用,來自洛斯阿拉莫斯國家實驗室(LANL)和倫敦大學的一項研究證明量子卷積神經網路(QCNN)具備巨大的潛力。
隨著量子計算機的出現給計算機領域帶來了許多突破性進展。在量子計算機上執行的卷積神經網路也因其比經典計算機更好地分析量子資料的潛力而引起諸多關注。量子神經網路(QNN)被認為是最有前途的架構之一,其應用包括物理模擬、最佳化等。
儘管 QNN 具有巨大的潛力,但許多 QNN 架構已被證明會出現「貧瘠高原」現象,其中代價函式的梯度隨系統大小呈指數級消失,使得 QNN 架構無法針對大型問題進行訓練。
近日,來自美國洛斯阿拉莫斯國家實驗室(LANL)和倫敦大學的研究人員構建了一個不存在貧瘠高原的特定 QNN 架構。該研究的論文《Absence of Barren Plateaus in Quantum Convolutional Neural Networks》在《PHYSICAL REVIEW X》上發表。
論文地址:https://journals.aps.org/prx/pdf/10.1103/PhysRevX.11.041011
近來一些研究者提出了量子卷積神經網路(QCNN)架構,洛斯阿拉莫斯國家實驗室(LANL)和倫敦大學的這項研究嚴格分析了 QCNN 架構中引數的梯度縮放。該研究發現梯度的方差消失的速度並沒有比多項式更快,這意味著 QCNN 沒有出現貧瘠高原現象。該結果為隨機初始化的 QCNN 的可訓練性提供了分析保證,這突出了 QCNN 與許多其他 QNN 架構的不同,即在隨機初始化下可訓練。
避免梯度消失問題
該研究為了得出其分析結果,提出了一種基於圖的新方法來分析 Haar 分散式 unitary 的期望值,這可能是一種極為有效的方法。最後,該研究用數值模擬驗證了其分析結果。
QCNN 架構
QCNN 架構涉及一系列卷積層和池化層,這些層減少了量子位元的數量,同時保留了有關資料特徵的資訊。
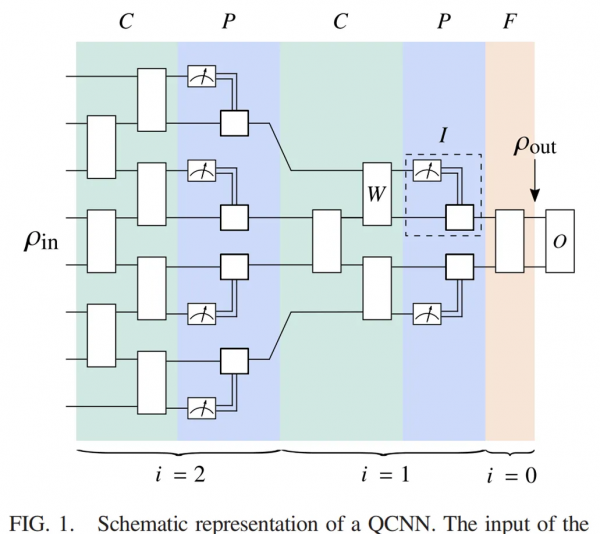
如下圖 1 所示,QCNN 架構將 Hilbert 空間 H_in 中的 n-qubit 輸入狀態 ρ_in 作為輸入,該狀態透過由一系列卷積層和池化層組成的電路傳送。卷積層由兩行引數化的雙量子位元門組成,作用於相鄰量子位元的 alternating 對。在每個池化層中,測量一半的量子位元,測量結果控制應用於相鄰量子位元的 unitary。在 L 個卷積層和池化層之後,QCNN 中還包含一個全連線層,該層對剩餘的量子位元應用 unitary。最後測量一些 Hermitian 運算元 O 的期望值。
QCNN 架構示意圖。
該研究將 QCNN 的輸入狀態對映到 Hilbert 空間中的一個縮減狀態,其中 H_out 的維度遠小於 H_in 的維度。輸出狀態可以表示為:
其中,V(θ)是包含卷積層和池化層以及全連線層中的門的 unitary,θ 是可訓練引數的向量,
表示除 H_out 中以外的所有量子位元的偏跡數(partial trace)。請注意,QCNN 中的非線性源於池化層中的池化運算元,這有效地降低了每一層的自由度。
代價函式
QCNN 的目標是應用一個訓練集 S(S 的大小 M=|S|),包含輸入狀態
來最佳化 QCNN 中的引數,並最小化代價函式,代價函式可表示為
其中 c_α是實係數,
是從如下等式 (1) 中獲得的,每個輸入狀態為ρ_in。
Ansatz
為了簡單起見,該研究主要考慮兩種情況:n=2^k 和 L=log(n)=k,這樣 dim(H_out)=2。此外,該研究假設卷積層和池化層中的 unitary 是獨立的。也就是說,V(θ) 中的卷積層和全連線層由作用於相鄰量子位元的兩個量子位元引數化 unitary 塊組成,表示為
。
研究者注意到,這種泛化包含作為特殊情況的常見 QCNN 結構,其中同一卷積或池化層中的塊是相同的。此外,研究者在論文的結果部分討論得出:卷積層中的 unitary 相關性往往會增加代價函式的梯度幅值。
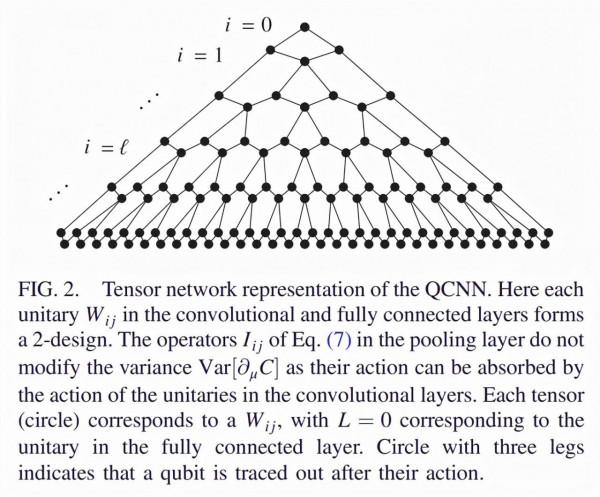
如上等式 (13) 所示,由於代價函式偏導數的方差獨立於 I_ij 中的受控 unitary,因此可以將池化層中運算元 I_ij 的作用附到卷積層中 unitary 的作用上。因此,QCNN 的張量網路表徵如下圖 2 所示。
QCNN 的張量網路表徵。
此外,該研究還提出了一種分析方差縮放的新方法,稱為 GRIM。
QCNN 架構的 GRIM 模組。
這項研究有什麼意義?
作為一種人工智慧方法,QCNN 受到視覺皮層的啟發,因此涉及一系列的卷積層與池化層,在保持資料集重要特徵的同時降低了資料的維度。這些神經網路可用於解決一系列問題,從影象識別到材料發現。克服貧瘠高原是挖掘量子計算機在人工智慧應用中的全部潛力並展示其優於經典計算機的關鍵。
Marco Cerezo(論文合著者之一)說,到目前為止,量子機器學習的研究人員分析瞭如何減輕貧瘠高原的影響,但他們缺乏完全避免它的理論基礎。LANL 的工作展示了一些量子神經網路實際上不受貧瘠高原的影響。
「有了這個保證,研究人員現在將能夠篩選關於量子系統的量子計算機資料,並將這些資訊用於研究材料特性或發現新材料等方面。」LANL 的量子物理學家 Patrick Coles 說。
40 多年來,物理學家一直認為量子計算機將被證明可用於模擬和理解粒子的量子系統,這會扼殺傳統的經典計算機。LANL 研究證明穩健的量子卷積神經網路型別有望在分析量子模擬資料方面獲得應用。
「關於鐳射有一句名言,當它們第一次被發現時,人們說它們是尋找問題的解決方案。現在到處都在使用鐳射。同樣,我們中的許多人懷疑量子資料能否變得高度可用,可能意味著量子機器學習也會起飛。」Coles 說道。
參考連結:
https://discover.lanl.gov/news/releases/1015-quantum-ai