原文連結: 新的計算方式 - EraDew
16世紀以後, 隨著天文、航海等領域的發展, 計算工作日趨繁重, 用羽毛筆在紙上完成這些計算不僅需要消耗大量的時間與精力, 而且非常容易出錯, 計算方式亟待改變. 一些天才科學家們開始思考是否能發明一些工具或方法來減少計算量, 由此開啟了一場簡化計算方式的探索.
1. 對數與對數表
對數是這場探索中最關鍵的成就, 它徹底改變了舊有的計算方式, 為天文、物理、航海等領域的發展做出了重大貢獻. 在介紹對數前, 我們有必要先花點時間瞭解下它的發明者 -- 約翰·納皮爾, 他是這場“計算革命”的核心人物.
1.1 約翰·納皮爾
約翰·納皮爾(John Napier, 1550年2月1日－1617年4月4日), 蘇格蘭數學家、物理學家兼天文學家.
圖 約翰·納皮爾(圖片來源於維基百科)
1550年納皮爾出生於蘇格蘭一個地位顯赫的家族, 他的父親是一位爵士, 母親是一位伯爵的女兒. 優越的家庭條件意味著小納皮爾有機會受到良好的教育, 幼年時期接受私人輔導, 13歲時進入聖安德魯斯大學並受到了校長的特別照顧. 由於當時蘇格蘭的大學教育質量較差, 納皮爾在舅舅的建議下從大學輟學並前往歐洲大陸繼續深造, 直到1571年返回蘇格蘭.
此後, 納皮爾過起了豐富而充實的蘇格蘭地主生活: 新建了一座與妻子居住的城堡、管理家族的莊園、參與地方和國家事務、參加宗教之間的爭論等. 在這些日常活動中納皮爾表現出了對科學探索的巨大熱情, 比如用礦物質施肥來提高田地的產量、為了防止蘇格蘭被入侵他設計了新的裝甲車以及遠距離對抗敵船的燃燒鏡, 如此等等, 不一而足.
不過在16世紀的蘇格蘭, 知識分子的興趣集中在宗教、神學和政治上, 而不是科學和數學上, 大環境如此納皮爾也不例外. 早在聖安德魯斯大學時, 納皮爾就對神學產生了濃厚的興趣, 以至於後來成為了一名狂熱的新教徒, 深入研究神學問題, 並於1593年發表了自認為最重要的作品《聖約翰全啟示錄》, 這本書被翻譯成荷蘭語、法語、和德語等共21個版本, 讓納皮爾作為學者和神學家獲得了相當大的聲譽.
與在神學上花費的精力相比, 納皮爾對數學的研究似乎只能看做是一種愛好, 然而這些“業餘時間”的研究卻成了他最矚目的成就.
1608年納皮爾在他的父親去世後, 搬入默奇斯頓居住, 成為那裡的第八任領主, 直到1617年去世.
圖 默奇斯頓城堡
1.2 對數的發明
納皮爾在進行數學計算時, 意識到大數的乘法、除法、平方等運算非常的繁瑣且需要耗費大量的時間, 因此開始考慮如何消除這些“障礙”. 為此他花費了很多精力來尋求簡化計算的方法, 最終找到了一些“簡短的規則”.
1614年, 64歲的納皮爾發表了著作《奇妙的對數表的描述》正式對外提出了對數的概念, 這本著作內含57頁關於對數的解釋和90頁的對數表.
圖 奇妙的對數表的描述
對數讓當時令人頭疼的大數的乘除等複雜運算得以簡化成加減運算. 如下的對數轉換公式你一定不陌生:
根據這兩個公式, 我們可以將大數的乘法和除法轉化成加法和減法, 配合對數表的使用便可以把繁瑣且容易出錯的複雜計算變成像查字典一樣的操作.
1.3 對數表
對數表是指把以某個數(比如10)為底的, 一定範圍內所有整數的對數值預先計算出來並編排入表格裝訂成的冊子, 就像一本提前計算好的“答案詞典”, 比如下圖中所示的六位對數表.
圖 一本六位對數表
用對數表計算時只需要從裡面查出標準答案即可, 有“查表”和“反查表”兩種常用操作. “查表”即查出某一個數的對數是多少, “反查表”則是已知一個數的對數查出這個數是多少. 下面我們舉例一個例子簡單說明下如何借用對數表來簡化計算.
比如我們借用對數表計算太陽的質量(思路源自知乎使用者童凌的回答: 對數是怎麼被髮明的?).
已知條件如下:
- 地球與太陽的距離:
- 地球公轉週期:
- 萬有引力常數:
- 太陽質量:
首先, 我們借用對數表, 把這個看起來很複雜的計算轉化成簡單的加減運算. 根據對數的轉換公式:
接下來進行查表, 比如我們查 π (取3.1416)的對數值. 如下圖所示, 找到對數表中3141所對應的行(紅色標註), 然後再找到下一位6所對應的列(藍色標註), 它們相交的位置就是31416所對應對數值的後4位7151, 加上前面的兩位“49”, 得到31416的對數值為497151(黃色標註的兩部分).
這時我們需進行一點常識性的估算來確定小數點的位置, 3.1416 介於0和10之間, 所以它的對數值應該介於0和1之間, 以此確定3.1416的對數值為0.497151.
圖 查表
按照同樣的方法, 我們查出其他的對數值如下:
代入Log(M)的計算公式可得:
接下來我們需要利用對數表查出誰的常用對數是298628, 也就是“反查表”操作. 如下圖所示, 由於對數表中的值是從小到大排序的, 我們可以先找到29開頭的部分, 再依次找到最接近298628的值: 298635(紅色標註), 它對應的真數是19890(黃色標註).
同樣我們需要確定小數點的位置, 0.298628的真數應該介於1~10之間, 所以為1.989, 最終求得月球質量約等於
圖 反查表
當查表和反差表的操作熟練到一定程度後, 大數的計算將會變得非常簡單, 大大減輕了各領域尤其是天文領域的計算量. 它的發明無疑是科學史上的一個大事件, 對於後來的天文學、力學、物理學的發展都非常重要, 尤其是天文學界以近乎狂喜的心情迎接這一發明, 比如伽利略就曾說:“給我空間、時間及對數, 我就可以創造一個宇宙!”, 同為天文學家的拉普拉斯認為: “對數透過減輕人工計算, 將天文學家的壽命延長了一倍”.
2. 納皮爾籌
前面提到約翰·納皮爾在簡化計算方面做出了很多努力, 除對數以外他還發明瞭一種由編號棒組成的計算工具. 這些編號棒由象牙製成, 因此看起來像骨頭, 所以後來被稱為“Napier's Bones”.
圖 一套1650年左右的納皮爾籌(圖片來源於維基百科)
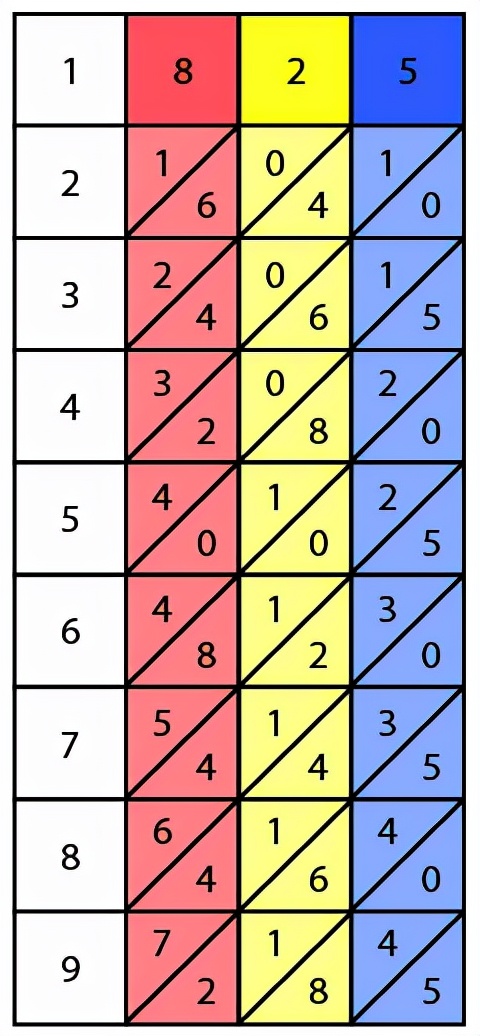
納皮爾籌由一個底座和一些方柱組成, 底座的左邊框標記著1至9, 每根方柱分為9格, 分別填著0至9與左邊框對應數字的乘積, 乘積的十位寫在斜線上方, 個位寫在斜線下方, 其示意圖如下.
圖 納皮爾籌示意圖(圖片來源於維基百科)
仔細觀察的話不難發現, 納皮爾籌實際上是一組拆分的九九乘法表, 透過組合、排列不同的方柱來組成不同的運算數, 下面我們以乘法運算來做說明.
2.1 格子乘法
納皮爾籌進行乘法運算是借用了“格子乘法”的原理, 這種乘法最早流行於十三世紀的阿拉伯, 十四世紀左右開始在歐洲流行起來.
“格子乘法”是一種利用帶斜線的格子進行多位數的乘法, 比如計算825×913, 步驟如下:
- 因為兩個乘數都是3位數, 所以畫出一個 3×3的表格.
- 畫出每個表格左下角到右上角的斜線, 然後在上面寫出825, 在右側寫出913.
- 上方的各個數字與右邊各個數字分別相乘, 乘得的結果填入格子裡, 十位在斜線上方, 個位在斜線下方, 比如第一行第一列 8×9=72, 則在斜線上方寫7下方寫2.
- 所有格子都填滿後, 從右下角開始按斜線行對應相加(斜線行結果左上方的小數字表示產生的進位).
- 按照從上到下, 再從左到右的順序列出每個斜線行的和, 就得到最終結果753225.
圖 格子乘法
2.2 用納皮爾籌計算
納皮爾籌就是把格子乘法中可能出現的結果事先刻在了方柱上, 然後選擇對應的柱子進行組合擺放來進行運算. 比如同樣計算825×913, 藉助納皮爾籌的步驟如下:
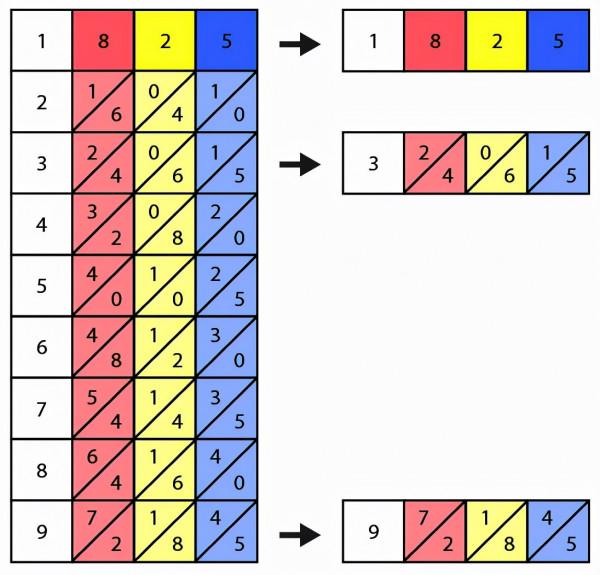
第一步: 取出8、2、5三根方柱, 放在底座上.
第二步: 分別找到9、1、3對應的行.
第三步: 按格子乘法, 分別得到9、1、3與825的乘積.
第四步: 將3行所得結果, 按數位對齊相加, 得到結果.
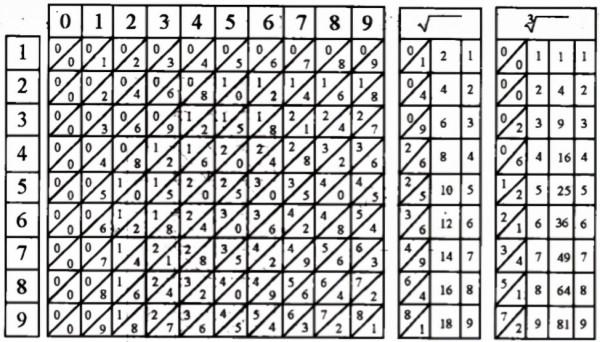
除了進行乘法運算之外, 納皮爾籌還可以進行除法、開方等更為複雜的運算, 開方運算需要用到另外一套專門的編號棒, 具體方法就不在此描述了.
圖 右側兩根分別用來計算平方根和立方根
納皮爾籌的發明引起了很大的反響, 以至於後來出現很多改進版. 德國圖賓根大學教授威廉·希卡德受到納皮爾的啟發, 發明了世界上第一臺機械計算器, 其乘法部分就是運用了改進後的納皮爾籌.
3. 計算尺
前文講到對數表把人們從繁瑣的筆算中解脫了出來, 但這帶來了另一個新的問題, 就是需要頻繁地查表. 查表是一項非常機械且枯燥的工作, 人們開始考慮是否能發明一種工具來進一步簡化查表的工作.
1620年, 英國數學家埃德蒙·甘特(Edmund Gunter)想到一種方案: 將對數值看作是一段長度, 那麼兩個對數的和就是兩段距離之和. 於是甘特把對數表上的值刻在了尺子上, 將對數值改成了直觀的刻度值, 查表的操作也相應地變成了測量距離, 後來這種尺子被稱為甘特尺.
圖 甘特尺(圖片來源於NathanZeldes的部落格)
甘特尺的計算需要藉助圓規來測量距離, 比如我們要計算2×3是多少, 根據對數的運算規則我們需要求log2+log3的值. 先用圓規測量出log2的長度, 再將圓規沿著尺子平移至log3的刻度, 相當於log3的長度加上之前用圓規測量的log2的長度, 此時圓規右腳所在的刻度就是最終的結果.
圖 用甘特尺計算2x3(圖片來源於NathanZeldes的部落格)
1622年, 另一位英國數學家威廉·奧特雷德(William Oughtred)對甘特尺進行了改進, 直接用另一把尺子代替了圓規, 將兩把尺子並排放置, 透過滑動來測量長度. 如下圖所示計算2×3, 滑動上尺, 將其1刻度與下尺的2處對齊, 找到上尺3的刻度, 對應的下尺刻度就是結果了.
圖 奧特雷德的計算尺(圖片來源於維基百科)
奧特雷德的計算尺雖然構思精巧、方便實用, 但最初並沒有引起廣泛傳播, 直到兩個多世紀以後, 1850年左右法國的炮兵中尉阿梅代·馬內姆(Amédée Mannheim)為了方便讀結果, 對計算尺進行了改進, 加上了一個遊標, 這種改造後的計算尺慢慢在歐洲普及起來.
其構造如下圖所示, 由三部分尺子和一個遊標組成, 上下兩部分尺子稱為定尺, 中間的尺子可以滑動稱為滑尺. 透明的遊標上一般有根中線, 用以對齊讀取計算結果.
圖 計算尺(圖片來源於SlideRuleMuseum)
在今天這種用物理量(長度、角度、電壓、電流等)來表示數字大小的計算方式稱為模擬計算, 現在計算尺可能很難買到了, 不過讀者可以訪問SlideRuleMuseum線上體驗虛擬計算尺, 用滑鼠可以移動滑尺和遊標. 此外, 如果讀者對計算尺的操作感興趣, 可以點選觀看這個影片, 瞭解如何用使用計算尺進行計算.
計算尺不僅能進行乘、除、乘方、開方, 甚至還可以計算三角函式、指數函式和對數函式, 因為價格低廉, 使用起來方便快捷, 在1970年代前被廣泛應用於各領域. 甚至一度成為工程師身份的象徵, 如同聽診器代表了醫學行業一樣, 即便是後來興起的各種半自動的機械計算機也沒能取代它的位置. 但是計算尺也有其自身的缺點, 它屬於模擬計算工具, 存在精度問題, 很難用於財務、統計等方面.
4. 本文小結
16世紀以後, 隨著天文、航海等科學領域的發展, 科學家們需要進行大量的複雜計算, 不僅繁瑣耗時還容易出錯, 人們急需新的計算方式. 在這樣的背景下, 同時身為天文學家和數學家的納皮爾發明了對數, 由此改變了科學領域的計算方式. 甘特在使用對數表計算的過程中想到用長度來表示對數值, 由此發明了最初的計算尺, 經過不斷的傳播與演變, 最終成為工程師們必備的計算工具, 為人類科學事業的發展做出了巨大貢獻.
相對於早期的算盤、算籌等工具來說, 對數表、納皮爾籌以及計算尺最明顯的進步就是把部分結果事先“準備”好了, 人們只需要根據規則進行查詢、組合或滑動, 就可以得到結果, 也就是說這些工具已經替我們完成了一部分計算工作, 進一步實現了計算的“自動化”, 為機械計算器的誕生奠定了基礎.
訪問原文連結: 新的計算方式 - EraDew 檢視計算機簡史系列全部文章
